- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
CalcPlot3D, an Exploration Environment for Multivariable Calculus - Tangent Planes
I develop the equation of a tangent plane early in order to help students understand the geometric meaning of the total differential. In my opinion, it is not very satisfying to determine the tangent plane to a surface at a given point if you cannot visually verify the answer.
When I assign these exercises, I usually require students to submit a print-out from the applet showing their tangent plane, the surface and the point of tangency.
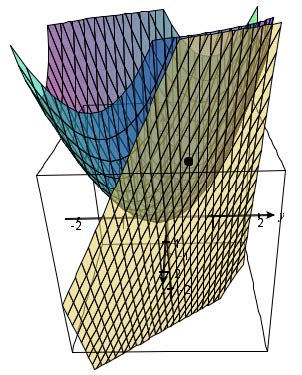
| Exercise: | Determine the tangent plane of the following surface at the point (1, 0.5) in its domain. Use CalcPlot3D to print the graph of this surface (with –2 to 2 on x- and y-axes) along with this tangent plane. Show the point of tangency. \[ z= f(x,y) = x^2 + xy + y^2 \] |
To create this plot, first enter the function in Function 1. Then enter the tangent plane function (solved for z) in Function 2. Graph these surfaces together. Then choose Add a Point from the Graph menu. Enter the coordinates of the point on the surface, and keep the default values for the other choices. To make it easier to see both surfaces, make them semi-transparent using either Ctrl-T or the Make Surfaces Transparent option on the View Settings menu.
Click here to open the CalcPlot3D applet in a new window.
Click here to open a pdf file which contains the instructions for the activity.
Answer: Tangent plane equation: \(z= 1.75 + 2.5(x - 1) + 2(y - 0.5)\)
Paul Seeburger (Monroe Community College), "CalcPlot3D, an Exploration Environment for Multivariable Calculus - Tangent Planes," Convergence (November 2011), DOI:10.4169/loci003781




