- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
CalcPlot3D, an Exploration Environment for Multivariable Calculus - Line of Intersection of Two Planes
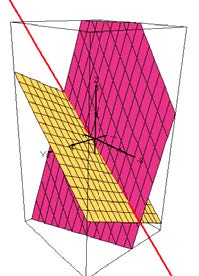 Visually verifying the line of intersection of two planes is another early topic where I get my students used to using the CalcPlot3D applet themselves. Below is an example of this type of problem:
Visually verifying the line of intersection of two planes is another early topic where I get my students used to using the CalcPlot3D applet themselves. Below is an example of this type of problem:
Exercise:
- Determine the line of intersection of the following two planes. Write the parametric equations for this line, showing all work. \[ 2x + y - 2x = 5 \qquad \& \qquad 3x-6y-2z=15 \]
- Use the CalcPlot3D applet to display these two planes. To do this, solve each planar equation for z, and enter them in Functions 1 and 2 on the left side of the 3D plot window. Zoom out a couple times (if necessary) until you can see both planes along with their intersection. Now add the line of intersection. (To do this, choose Add a Space Curve from the Graph menu, and enter the parametric equations for the line.) Rotate the 3D view to verify that your line is indeed the intersection of the two planes. Rotate until you have a good view of the two planes and the line of intersection. Use the Print Graph menu option on the File menu at the top left corner of the applet to print out your resulting view and hand this printout in with this assignment.
Click here to open the CalcPlot3D applet in a new window.
Click here to open a pdf file which contains the instructions for the activity.
| Answer Line: | \(x = 3+14t\) | Here are the plane equations, solved for z: | |
| \(y=-1+2t\) | \(z=(2x+y-5)/2\) | ||
| \(z=15t\) | \(z=(3x-6y-15)/2\) |
Paul Seeburger (Monroe Community College), "CalcPlot3D, an Exploration Environment for Multivariable Calculus - Line of Intersection of Two Planes," Convergence (November 2011), DOI:10.4169/loci003781




