- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Origin of the Prime Number Theorem: A Primary Source Project for Number Theory Students
Near the end of the eighteenth century, Adrien-Marie Legendre (1752–1833) and Carl Friedrich Gauss (1777–1855) seemingly independently began a study of the primes—more specifically, of what we now call their density. It would seem fairly clear to anyone who considered the matter that prime numbers are more rare among larger values than among smaller ones, but describing this difference mathematically seems not to have occurred to anyone earlier. Indeed, there's arguably no a priori reason to assume that there is a nice function that describes the density of primes at all. The mini-Primary Source Project (PSP) The Origin of the Prime Number Theorem provides students with an introduction to this problem through the writing of Gauss and Legendre.
Late in his life (Christmas Day, 1849), Gauss wrote a letter to his colleague Johann Encke (1791–1865) about prime numbers. He reported that he had been interested in primes when he was young, and that in fact he had both tabulated the number of primes in various intervals himself, and then spent some time studying a table of primes that had recently been compiled by Johannn Lambert (1728–1777). As early as 1792 or 1793, Gauss claimed, he had conjectured that the number of primes below a bound \(n\) was, in his notation, \(\int \frac{dn}{\log n}\).
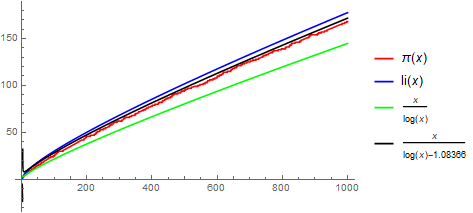
Today we know that Gauss was correct, but we write his conjecture differently. Using more modern notation, and letting as usual \(\pi(x)\) denote the number of primes less than or equal to \(x\), we have
\[\pi(x) \sim \int_2^x \frac{dt}{\log t} \sim \frac{x}{\log x}.\]
(The function \(\mbox{li}(x) = \int_2^x \frac{dt}{\log t} \) is often referred to as the logarithmic integral. The notation \(f(x) \sim g(x)\) indicates that \(\lim_{n \to \infty} \frac{f(x)}{g(x)} = 1\).)
|
|
Gauss told no one at the time that he was thinking about prime numbers, and thus Legendre, in the second edition of his Essai sur la Théorie des Nombres (Essay on Number Theory) [Legendre 1808], had good reason to suspect he was the first person to consider the question of the number of primes below a given bound. He began by noting one of the greatest puzzles in modern number theory–the sequence of primes is indeed "extremely irregular," and seems almost random on a small scale, but on a larger scale they seem to follow a rather predictable pattern. Here is how Legendre described this pattern (the English translation is mine):
On a very remarkable law observed in the enumeration of prime numbers
Although the sequence of prime numbers is extremely irregular, one can however find, with a very satisfying precision, how many of these numbers there are from \(1\) up to a given limit \(x\). The formula that resolves this question is
\[y = \frac{x}{\log(x) - 1.08366} \ldots.\]
Legendre then presented a table comparing the values predicted by his formula with the true count, as determined by a recently-published table of primes (Juri Vega's Thesaurus logarithmorum [Vega and Vlack 1794]).

Gauss claimed merely to have looked at the data and seen the pattern; his complete statement reads "I soon recognized that behind all of its fluctuations, this frequency is on the average inversely proportional to the logarithm." Legendre gave even less indication of the origin of his estimate; in particular, his rather precise constant of \(1.08366\) has, as far as I know, never been satisfactorily explained. In the mini-PSP The Origin of the Prime Number Theorem, students explore how Legendre and Gauss may have arrived at their conjectures, compare the similar (though not identical) estimates for the number of primes up to \(x\) given by each, and examine some of the ideas related to different formulations of the Prime Number Theorem. Using the letter written by Gauss, they then examine the error in their respective estimates.
The complete project The Origin of the Prime Number Theorem (pdf) is ready for student use and the LaTeX source code is available from the author by request. Instructor notes are provided to explain the purpose of the project and guide the instructor through implementation of the project.
This project is the ninth in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series appear below, including two additional mini-PSPs in number theory. The full TRIUMPHS collection also offers several more extensive “full-length” PSPs for use in teaching number theory.
Acknowledgments
The development of the student project The Origin of the Prime Number Theorem has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.
References
Legendre, Adrien-Marie. 1808. Essai sur la théorie des nombres. 2nd ed. Paris: Courcier.
Vega, George, and Adriaan Vlack. 1794. Thesaurus logarithmorum completus: ex Arithmetica Logarithmeticam, et ex Trigonometria Artificiali Adriani Vlacci collectus, etc. / Vollständige Sammlung Grösserer Logarithmisch-trigonometrischer Tafeln nach Adrian Vlack’s Arithmetica Logarithmetica und Trigonometria Artificialis (Complete collection of logarithmic-trigonometric tables, from the Arithmetica Logarithmica and Trigonometria Artificialis of Adrian Vlack, etc.). Weidmannschen Buchhandlung.
Dominic Klyve (Central Washington University), "The Origin of the Prime Number Theorem: A Primary Source Project for Number Theory Students," Convergence (March 2019), DOI:10.4169/convergence20190301