- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Beyond Riemann Sums: Fermat's Method of Integration – A Mini-Primary Source Project for First-Year Calculus Students
For those of us who have studied (or taught) calculus for years, the idea of approximating the area under a curve with Riemann sums may seem so self-evident as to not merit much consideration. What could be simpler than starting with an interval, splitting it into subintervals of equal size, and finding an approximation to the area under the curve over each of these intervals? On the other hand, might there exist other methods that are historically-grounded and ripe for student exploration? The rhetorical nature of the previous questions being obvious, the reader will not be surprised to know that the answer is “yes—and this article introduces a mini-Primary Source Project (mini-PSP), Beyond Riemann Sums: Fermat's Method of Integration, designed to introduce students in a first course on integration to one such method.”
Of course, if a curve has properties that make it behave differently over different areas of its domain, we might start to guess that there could be a more clever method to estimate this area. Indeed, many areas of mathematical modeling, numerical analysis, or statistics rely on the idea that approximating methods can “zoom in” to areas where a lot of change happens, but give coarser approximations when the underlying curve (or model) is more static. Perhaps, a historian might speculate, after Riemann gave us regular intervals, another mathematician proposed a method that bases the size of the approximating rectangles on the absolute value of the derivative of the function to be approximated, as shown in the following figure.
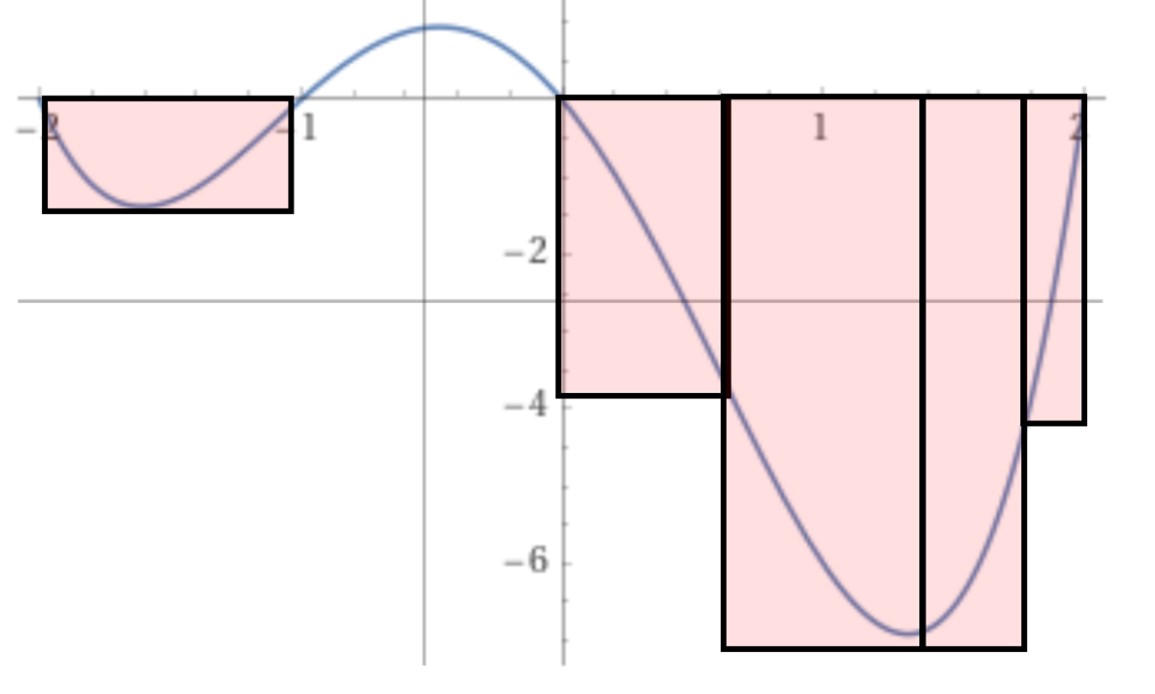
Finding a lower bound on \(\int_{-2}^2 f(x) dx\) using rectangles of variable width.
Image created by the author.
However, in one of those twists that seems to be common in the history of calculus, the first proposal to find the area under a curve using rectangles of different sizes came not after Riemann, but before him. Indeed, before Euler, and before even Newton and Leibniz, Pierre de Fermat (1601–1665) proposed a method to find the “quadrature”—what we might now call the area under the curve—of the generalized hyperbola \(1/x^n\).
This mini-PSP walks students through Fermat’s method by using excerpts from his “Treatise on Quadratures”1 [Fermat 1679]. There are some challenges to reading Fermat’s work. Since it predates both the notion of the integral and function notation, Fermat worked only geometrically. However, what we lose from convenient notation we may gain from the understanding that comes through geometric reasoning. The project begins with Fermat’s discussion of the convergence of a geometric series, and then it introduces the method he used to find the area under a hyperbola using rectangles of different widths. Students are encouraged to use geometric thinking to find the area of these rectangles, and from these areas to deduce a conclusion about the area under the curve. In addition to seeing a nice example of mathematical invention as they explore Fermat’s clever trick, it is hoped that students will benefit from seeing all the main ideas of Riemann integration in this new, somewhat alien setting.
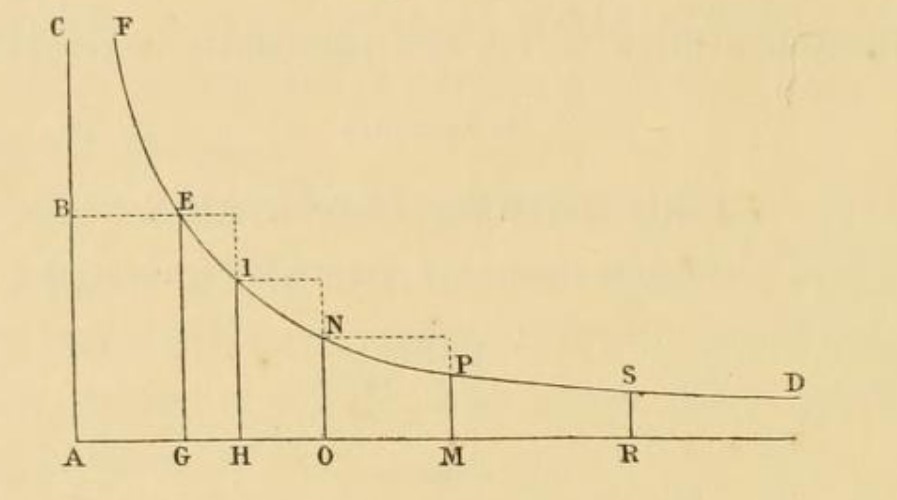
Fermat’s rectangles of different widths for estimating the area under a hyperbolic curve, from [Fermat 1679, p. 45].
The complete project Beyond Riemann Sums: Fermat's Method of Integration (pdf) is ready for student use and the LaTeX source code is available from the author by request. Instructor notes are provided to explain the purpose of the project and guide the instructor through implementation of the project.
This project is the twenty-eighth in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first-year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series, including 14 additional projects for use in introductory calculus courses, appear below. The full TRIUMPHS collection also offers two other mini-PSPs and six more extensive “full-length” PSPs for use in teaching calculus.
Recommendations for Further Reading
Without a doubt, the most thorough study of Fermat’s work is Michael Sean Mahoney’s The Mathematical Career of Pierre de Fermat (1601–1665) [Mahoney 1994]. Mahoney’s discussion of Fermat’s “Treatise on Quadrature” begins on page 243 of his book. The earliest discussion I could find in print of Fermat’s integration techniques is [Boyer 1945], which should be read by anyone looking to understand the history of our understanding of Fermat’s work. For a discussion of how Fermat’s work can be used in the classroom using modern notation, see [Rickey 2023] and [Shell-Gellasch 2011].
Acknowledgments
The development of the student project Beyond Riemann Sums: Fermat's Method of Integration has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grant No. 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.
References
Boyer, Carl B. 1945. Fermat's Integration of xn. National Mathematics Magazine 20:29–32.
Fermat, Pierre de. 1679. De aequationum localium transmutatione, & emendatione, ad multimodam curvilineorum inter se vel cum rectilineis comparationem, cui annectitur proportionis geometricae in quadrandis infinitis parabolis et hyperbolis usus. In Varia opera mathematica D. Petri de Fermat, 44–57. Toulouse: Johannes Pech.
Mahoney, Michael S. 1994. The Mathematical Career of Pierre de Fermat, 1601–1665. Princeton: Princeton University Press.
Rickey, V. Frederick. 2023, May. Historical Notes for the Calculus Classroom: Fermat’s Integration of Powers. Convergence.
Shell-Gellasch, Amy. 2011. Integration à la Fermat. In Mathematical Time Capsules: Historical Modules for the Mathematics Classroom, edited by Amy Shell-Gellasch and Dick Jardine, MAA Notes, 77:111–116. Washington, DC: Mathematical Association of America.
[1] As was not unusual for 17th-century works, the full title is quite long: “De aequationum localium transmutatione, & emendatione, ad multimodam curvilineorum inter se vel cum rectilineis comparationem, cui annectitur proportionis geometricae in quadrandis infinitis parabolis et hyperbolis usus,” which Mahoney translates as “On the transformation and alteration of local equations, for the purpose of variously comparing curvilinear figures among themselves or to rectilinear figures, to which is attached the use of geometric proportions in squaring an infinite number of parabolas and hyperbolas” [Mahoney 1994, p. 245].
Dominic Klyve (Central Washington University), "Beyond Riemann Sums: Fermat's Method of Integration – A Mini-Primary Source Project for First-Year Calculus Students," Convergence (August 2023), DOI:10.416920230801




