- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 9
The integral \[\int \frac{dx}{\sqrt{A+Bx+Cx^2}}\] is more sophisticated still. Try to prove for yourself that, if \(C>0\), \[\int \frac{dx}{\sqrt{A+Bx+Cx^2}}= \frac{1}{\sqrt{C}} \log\left ( 2Cx+B+\sqrt{4C(A+Bx+Cx^2)} \right ).\] In his Calculus, letting \(A=0\), \(B=2a\), and \(C=1\), De Morgan deduced that, as he put it: \[\int \frac{dx}{\sqrt{2ax+x^2}}= \log \left( x + a + \sqrt{(2ax+x^2)} \right ) + \log 2. \mbox{ (Omit the constant.) } \]
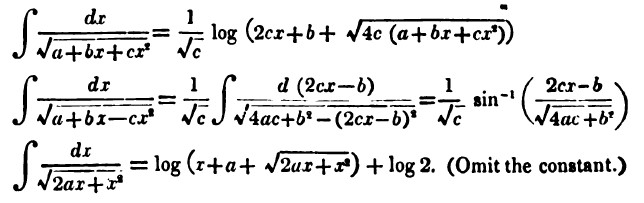
Figure 11. Part of page 116 from De Morgan’s Differential and Integral Calculus.
But when Lovelace tried to derive this result from first principles, she wrote [LB 170, 15 Aug. [1841], f. 115v]:
I cannot make it anything but \[\int \frac{dx}{\sqrt{2ax+x^2}} = \log \left ( x + 2a + \sqrt{(2ax+x^2)} \right )\] or else \[ = \log \left ( \frac{x}{2} + a + \frac{\sqrt{2ax+x^2}}{2} \right )+ \log 2 \] \(\ldots\) and I begin to suspect the book.
Her approach was straightforward. Setting \(2ax+x^2=(2a+x)x=y^2\), she derived the differential equation \((2a+x)dx=ydy\), from which she formed the integral \[\int \frac{dx}{y}=\int \frac{dy}{2a+x} .\]
Then, by analogy with the ‘fact’ that \(\frac{dx+dy}{x+y}=\frac{dx}{y}\), she obtained \[ \begin{array}{lcl} \int \frac{dx}{y} &=& \int \frac{d(2a+x)+dy}{(2a+x)+y}\\ &=&\int \frac{d(2a+x+y)}{2a+x+y}\\ &=&\log(2a+x+y)\\ &=&\log(2a+x+\sqrt{2ax+x^2})\\ &=& \log\left ( \frac{x}{2} + a + \frac{\sqrt{2ax+x^2}}{2}\right )+\log 2.\end{array}\]
In addition to her erroneous assumption that \[\frac{dx+dy}{x+y}=\frac{dx}{y}\]
De Morgan was able to spot that, given \(y^2=(2a+x)x\), she had forgotten to apply the product rule, so that her differential equation should have been \[ydy=\frac{1}{2} xdx + \frac{1}{2} (2a+x)dx \] or \[ydy=(x+a)dx.\,\,\,\,\, \mbox{[2]}\] After correcting these errors, Lovelace wrote in a subsequent letter [LB 170, 21 Aug. [1841], f. 121v], that
we arrive then in my corrected paper, at \[\begin{array}{rcl}\int \frac{dx}{\sqrt{2ax+x^2}} &=& \log \left( x + a + \sqrt{(2ax+x^2)} \right )\\ &=&\log\left( \frac{x}{2} + \frac{a}{2} + \frac{\sqrt{2ax+x^2}}{2} \right )+\log 2.\end{array}\]
Can you derive Lovelace’s final result from equation [2]?
In his acknowledgement, De Morgan observed that Lovelace’s answer agreed with his result in all respects ‘but the log 2, which being a Constant, matters nothing’ [LB 170, 21 Aug. [1841], f. 121v]. Explain why his and Lovelace’s results are equivalent.
Adrian Rice (Randolph-Macon College), "Helping Ada Lovelace with her Homework: Classroom Exercises from a Victorian Calculus Course – Problem 9," Convergence (September 2021)




