- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Thinking Outside the Box -- or Maybe Just About the Box
Introduction
Perhaps one of the deepest entrenched calculus problem is the canonical box problem that students encounter when discussing applied extrema problems. In fact, Friedlander and Wilker (1980) commented, ''This question must be answered nearly a million times a year by calculus students from every corner of the globe'' (p. 282). Without a doubt, almost every recently published calculus text contains a problem similar to the following:
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. Congruent squares are to be cut from its four corners. The resulting piece of cardboard is to be folded and its edges taped to form an open-topped box (see figure below). How should this be done to get a box of largest possible volume?
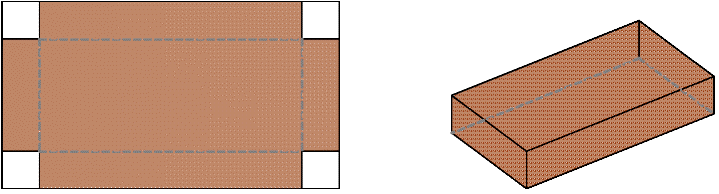 Figure 1: Canonical Box Problem
Figure 1: Canonical Box Problem
In particular, this problem (or some derivative of it) occurs in a classic text such as Thomas (1953) as well as modern texts such as Stewart (2008), Larson, Hostetler and Edwards (2007) and Smith and Minton (2007). But, what about this problem makes it so common and prevalent to the calculus experience? This paper takes a closer look at this common box problem and asks some difficult questions:
- Does this box problem really reflect reality?
- Is there a better box problem more consistent with modern box building techniques? And
- Can a better box problem be explored by Calculus 1 students in a single variable course?
If you enjoy this canonical box problem, we developed a Java Sketchpad applet, called OpenBox, for this problem. For this applet, the yellow points are moveable and control the size of the sheet of cardboard and the position of the cut. A dynamical graphic contained in a grey box shows the graph of the Volume to cut length (x) function. In addition, a dynamical picture of the open box is provided to illustrate how the changes in cut length impacts the configuration of the open box. (Warning: The
Thomas Hern (Bowling Green State Univ.) and David Meel (Bowling Green State Univ.), "Thinking Outside the Box -- or Maybe Just About the Box," Convergence (February 2010), DOI:10.4169/loci003321




