- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Teaching and Learning the Trigonometric Functions through Their Origins: Episode 5 – al-Bīrūnī Does Trigonometry in the Shadows
It is generally well known that in the history of trigonometry, sine (and cosine) arose as adaptations, by Hindu astronomer-priests of the first millennium CE, of the earlier Greek notion of the chord of an arc in a circle. Since applications for which these chord lengths were needed often required determining half the chord of the doubled arc, in order to solve a certain right triangle, it was more useful to tabulate half-chords instead. Thus, the Hindu sine took on a life of its own; the cosine was nothing more than the sine of the complementary arc.

But what about the tangent, cotangent, secant and cosecant, to round out this trigonometric zoo of functions? How did these four trigonometric quantities arise?[1] It will come as no surprise to those familiar with the quirks of history that the Latin-based names we give them today were assigned centuries after they were first tabulated. The classroom unit al-Bīrūnī Does Trigonometry in the Shadows offered here employs excerpts from a text dating back to the golden era of Islamic mathematics to introduce students to the genesis of these quantities.
A scholar known mostly for his expertise in Hindu culture and science, Abū Rayhan Muhammad ibn Ahmad al-Bīrūnī (973–1048) wrote The Exhaustive Treatise on Shadows in 1021, exactly 1000 years before the preparation of this classroom unit. In Shadows, he provided a geometric and numerical analysis of the relation between the length of the shadow cast by a simple gnomon sundial and the corresponding arc of elevation of the Sun. Al-Bīrūnī considered two kinds of gnomon, one in which the gnomon is erected perpendicular to the ground, casting a “direct shadow,” and another in which the gnomon is mounted horizontally on a vertical wall, casting its “reversed shadow” on the wall itself. These shadow lengths, tabulated by al-Bīrūnī for a gnomon of unit length, are the quantities which centuries later would be renamed ‘cotangent’ and ‘tangent’, respectively.
The classroom unit opens with this simple problem of timekeeping based on shadows cast by the Sun. Students encounter al-Bīrūnī’s geometrical model for the shadow-casting gnomon, which makes it plain how the lengths of shadows are modeled by sides of right triangles and how tabulation of their lengths would be useful for more accurate daylight timekeeping. This realistic setting forms the foundation for what would later crystalize into the trigonometric quantities of tangent, cotangent, secant and cosecant. Examples of how al-Bīrūnī may have used this trigonometry to deal with the practical use of a shadow-casting clock are included throughout so that the mathematics is never too far from the astronomical context in which it arose.

A simple gnomon sundial.
Photo by Rich Luhr, reproduced under Creative Commons license BY-NC-ND 2.0.
This classroom unit is one of a series of six units in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins that attempts to provide students with a rich motivation for the study of trigonometry by presenting a series of episodes from the long history of the subject. These episodes work to contextualize the main ideas of trigonometry in the questions that earlier mathematicians addressed in developing the subject over thousands of years.
The unit al-Bīrūnī Does Trigonometry in the Shadows (pdf) is ready for student use. It is meant to be completed in two 50-minute classroom periods, plus time in advance for students to do some initial reading and time afterwards for them to write up their solutions to the tasks. A brief set of instructor notes offering additional background and practical advice for the use of these materials in the classroom is appended at the end of the student version of these projects.
al-Bīrūnī Does Trigonometry in the Shadows is the fifth in the Convergence series Teaching and Learning the Trigonometric Functions through Their Origins. Although these classroom projects are posted here as parts of a series, each episode has been redesigned to stand alone. Readers who want to see the entire Primary Source Project (PSP) from which these units are drawn can obtain that PSP, A Genetic Context for Understanding the Trigonometric Functions, without waiting for future installments to appear, from the website of the NSF-funded project TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS). The LaTeX source code of all TRIUMPHS projects, including the units to appear in this series, are available from the project authors by request.
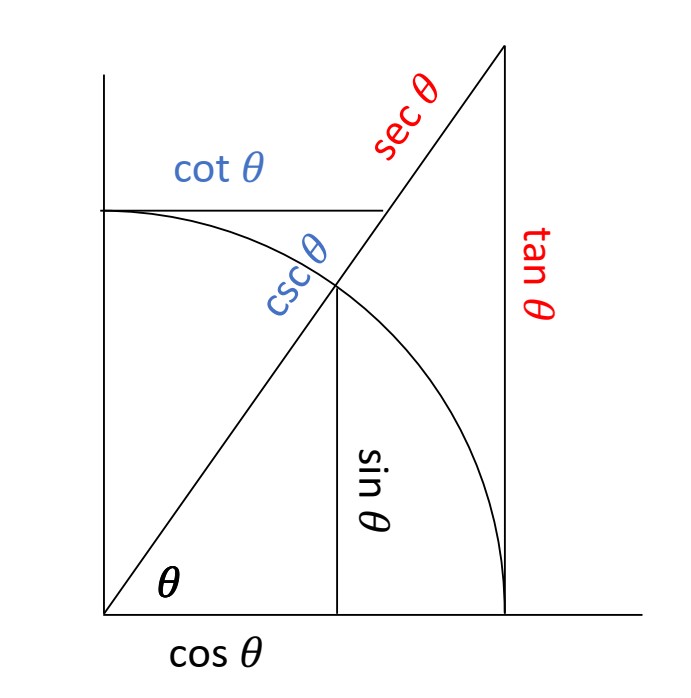
[1] I remember first considering this question myself, and I leapt to the natural conclusion that, because of how they were named, they must have identified other lines in the geometry of arcs in a unit circle. I recall learning to associate the trigonometric quantities with the segments in a diagram that combined three right triangles containing the same angle \(\theta\) (see the diagram below): one triangle inside the circle with hypotenuse equal to the unit radius and whose sides were the sine and cosine; one with base \(1\), whose side and hypotenuse are the tangent and secant; and one with vertical side \(1\) (so that the angle at the origin is complementary to \(\theta\)), whose side and hypotenuse are the cotangent and cosecant. While the names we give these segments today are related to how they appear in the diagram below, these quantities have a much older pedigree.
Daniel E. Otero (Xavier University), "Teaching and Learning the Trigonometric Functions through Their Origins: Episode 5 – al-Bīrūnī Does Trigonometry in the Shadows," Convergence (September 2021)




