- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
A Selection of Problems from A.A. Markov’s Calculus of Probabilities: Andrei Andreevich Markov
Andrei Andreevich Markov was born on June 14, 1856, in Ryazan Gubernia (governorate, similar to a state in the US) in Russia, the son of Andrei Grigorevich Markov, a successful lawyer. He graduated from the gymnasium (high school) in 1874 and enrolled in Petersburg University, where he received a gold medal for his work, On Integration of Differential Equations with the Help of Continued Fractions.
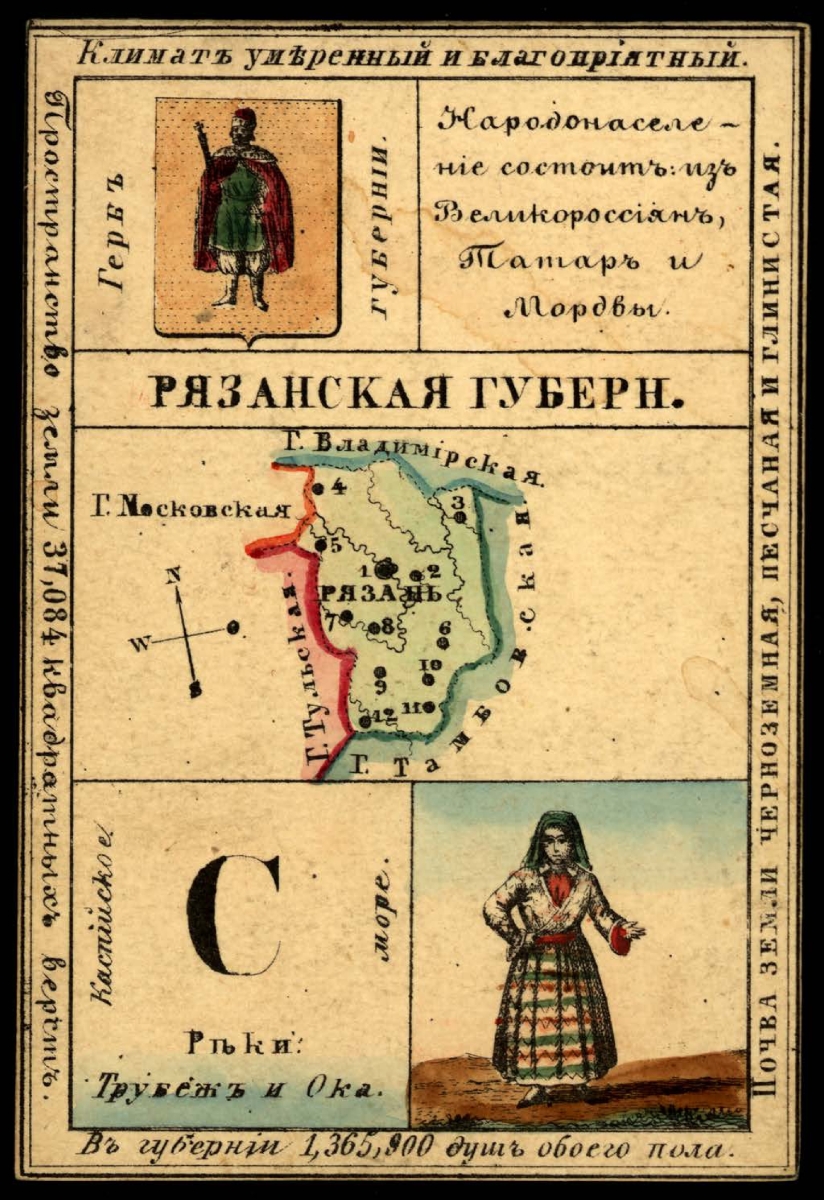
Figure 2. A card from a geographical card set with a map of Ryazan Gubernia in 1856
and the governorate located within the Russian Empire as it existed in 1914.
Wikimedia Commons, public domain and created by Milenioscuro, CC BY-SA 4.0 DEED.
He defended his master’s degree dissertation, On Binary Quadratic Forms with Positive Determinant, in 1880, under the supervision of Aleksandr Korkin (1837–1908) and Yegor Zolotarev (1847–1878). He then wrote his doctoral dissertation, On Some Applications of Algebraic Continued Fractions, under the supervision of Pafnuty Lvovich Chebyshev (1821–1894), in 1884. Markov taught at Petersburg University until 1905, but he continued to conduct research there until his death from sepsis after an operation on his leg on July 20, 1922.
Markov married Maria Ivanova Valvatyeva in 1883. They had one son, also named Andrei Andreevich Markov (1903–1979), who became a mathematician, noted for his work in constructive mathematics and logic. In 1951, the younger Andrei wrote a book, Selected Works (Избранные Труды), containing some of his father’s contributions to mathematics.
At some point in the 1890s, Markov became interested in probability, especially limiting theorems of probabilities, laws of large numbers and least squares (which is related to his work on quadratic forms). One point of emphasis was on generalizations of the Central Limit Theorem, where he eventually weakened the independence requirement, replacing it with dependence of each variable only on its immediate predecessor. This ultimately led to his work on what would be known later as Markov chains in 1906.2 Specifically, a Markov chain is a discrete-state stochastic process \(\{X_1,X_2,X_3,\ldots,\}\) in which the probability mass function of \(X_n\) depends only on the value of \(X_{n-1}\) and not on the values of any previous variables; that is, \(P(X_n=j|X_{n-1}=i, X_{n-2}, X_{n-3},\ldots)=P(X_n=j|X_{n-1}=i)=p_{ij}\). The first use of the term “Markov chain” was most likely by Sergei N. Bernstein (1880–1968) in [Bernstein 1927].
[2] For more information on the development of Markov chains, see [Basharin et al. 2004] and [Seneta 1996].
Alan Levine (Franklin and Marshall University), "A Selection of Problems from A.A. Markov’s Calculus of Probabilities: Andrei Andreevich Markov," Convergence (November 2023)




