Mathematics Magazine - June 2016

The June issue is here with articles on varied topics, perfect for summer reading. Roger Nelsen investigates multi-polygonal numbers. Bijections, permutations, and cycles are used by Pozdnyakov and Steele to analyze changing seats on a bus. Gary Brookfield tests your intuition on cyclotomic polynomials.

 

Other articles examine the binomial recurrence, the Symmedian point, a classic calculus problem involving a Diophantine equation, Morrie’s law, and a relationship between GCDs and LCMs. This issue marks the return of both the art interview (of Robert Fathauer) and the crossword puzzle (on MathFest). Reviews and Problems round out the issue. Happy reading.

—Michael A. Jones, Editor

JOURNAL SUBSCRIBERS AND MAA MEMBERS:

To read the full articles, please log in to the member portal by clicking on 'Login' in the upper right corner. Once logged in, click on 'My Profile' in the upper right corner.

Vol. 89, No. 3, pp 157 – 232

Articles

Multi-Polygonal Numbers

Robert B. Nelsen

We study some sequences of multi-polygonal numbers, specifically the square triangular, oblong triangular, pentagonal triangular, and pentagonal square numbers. To do so, we state and prove theorems that relate the factors of a given triangular number to a pair of larger triangular numbers with a triangular sum, and relate a triangular number that is three times another triangular number (or three times a square) to a larger pair of triangular numbers with the same property.

To purchase from JSTOR: 10.4169/math.mag.89.3.159

Proof Without Words: Every Cobalancer Is a Balancing Number

G. K. Panda and Ravi Kumar Davala

A visual proof that every cobalancer is a balancing number.

To purchase from JSTOR: 10.4169/math.mag.89.3.165

Buses, Bullies, and Bijections

Vladimir Pozdynakov and J. Michael Steele

The random—or orderly—seating of passengers on a bus is used to motivate several questions about cycles of permutations. These in turn motivates the investigation of bijections between special subsets of permutations. The goal, of course, is to give simple explanations of surprising facts.

To purchase from JSTOR: 10.4169/math.mag.89.3.167

Proof Without Words: Limit of a Recursive Root Mean Square

Ángel Plaza

Visual proof that the limit of the recursive root mean square sequence defined by a_{n + 1} where a₁ and a₂ are the initial values of the sequence.

To purchase from JSTOR: 10.4169/math.mag.89.3.177

The Coefficients of Cyclotomic Polynomials

Gary Brookfield

One of the most surprising properties of cyclotomic polynomials is that their coefficients are all 1, -1 or zero—at least that seems to be the case until one notices that the 105th cyclotomic polynomial has a coefficient of -2. This article serves as an introduction to these polynomials with a particular emphasis on their coefficients and proves that the coefficients of the first 104 cyclotomic polynomials are at most one in absolute value.

To purchase from JSTOR: 10.4169/math.mag.89.3.179

Proof Without Words: Limit of a Recursive Arithmetic Mean

Ángel Plaza

Visual proof that the limit of the recursive arithmetic mean sequence defined by is 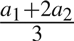, where a₁ and a₂ are the initial values of the sequence.

To purchase from JSTOR: 10.4169/math.mag.89.3.189

A Curious Result for GCDs and LCMs

Jathan Austin

We give necessary and sufficient conditions under which the sum of two positive integers equals the difference of their least common multiple and greatest common divisor, and then prove this result.

To purchase from JSTOR: 10.4169/math.mag.89.3.190

Proof Without Words: Sums of Powers of ⁴⁄₉

Tom Edgar

We provide a visual computation of a particular infinite series.

To purchase from JSTOR: 10.4169/math.mag.89.3.191

The Binomial Recurrence

Michael Z. Spivey

We give a new, direct argument that the solution to the binomial recurrence is the binomial coefficient. Our argument does not assume that the solution is known in advance nor does it rely on anything other than basic properties of two-variable triangular recurrence relations.

To purchase from JSTOR: 10.4169/math.mag.89.3.192

Proof Without Words: Sums of Consecutive Odds and Positive Integer Cubes

Stanley R. Huddy

To purchase from JSTOR: 10.4169/math.mag.89.3.196

An Algebraic Method to Find the Symmedian Point of a Triangle

M. Bani-Yaghoub, Noah H. Rhee and Jawad Sadek

A relationship between the symmedian point of a triangle and the least-squares solution of a linear system is presented. The coordinates of the symmedian point are explicitly calculated as a solution to the linear system.

To purchase from JSTOR: 10.4169/math.mag.89.3.197

Building the Biggest Box: Three-factor Polynomials and a Diophantine Equation

Gregory Convertito and David Cruz-Uribe, OFS

We consider a well known calculus question, and show that the solution of this problem is equivalent to finding integer solutions to a Diophantine equation. We generalize the calculus question, which in turn leads to a more general Diophantine equation. We give solutions to all of these and describe some of the historical background.

To purchase from JSTOR: 10.4169/math.mag.89.3.201

Proof Without Words: Sums of Reciprocals of Binomial Coefficients

Tom Edgar

We provide a visual computation of the sum of the series obtained by adding the reciprocals of entries from column n from Pascal's triangle.

To purchase from JSTOR: 10.4169/math.mag.89.3.212

A Geometric Proof of a Morrie-Type Formula

Samuel G. Moreno and Esther M. García-Caballero

We use a regular heptagon to give a geometric proof of a specific instance of a Morrie-type formula.

To purchase from JSTOR: 10.4169/math.mag.89.3.214

Proof Without Words: Viviani for Congruent Cevians

Grégoire Nicollier

We prove without words that the distances from the sides of a triangle measured parallelly to three congruent cevians sum up to the cevian length. This generalizes Viviani′s theorem about the sum of the distances from the sides of an equilateral triangle.

To purchase from JSTOR: 10.4169/math.mag.89.3.216

Crossword Puzzle: MathFest 2016

Brendan Sullivan

To purchase from JSTOR: 10.4169/math.mag.89.3.218

Robert Fathauer: Polymath Purveyor

Amy L. Reimann and David A. Reimann

To purchase from JSTOR: 10.4169/math.mag.89.3.220

Problems and Solutions

Proposals, 1996-2000

Quickies, 1061-1062

Solutions, 1966-1970

Answers, 1061-1062

To purchase from JSTOR: 10.4169/math.mag.89.3.223

Reviews

Math circles; ageism in mathematics, mathematics in movies

To purchase from JSTOR: 10.4169/math.mag.89.3.231