- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Pierre-Simon Laplace, 1749-1827: A Life In Exact Science

Publisher:
Princeton University Press
Publication Date:
1997
Number of Pages:
322
Format:
Hardcover
Price:
49.50
ISBN:
978-0691011851
Category:
General
[Reviewed by , on ]
Stacy G. Langton
04/8/1999
Writing the biography of a mathematician poses special problems. Richard Westfall's magnificent biography of Newton, Never At Rest, gives a revealing picture of a most unusual personality, from the windmill he made as a boy to his domination of the Royal Society as an old man. But there is something wrong with the sections in which Westfall describes Newton's mathematics. I thought at first that it was just my own stupidity that I couldn't make sense out of Westfall's account. But when I looked up Newton's own words in D. T. Whiteside's edition of Newton's Mathematical Papers, I saw what had happened. Westfall had copied out only part of what Newton had written. (He had also omitted Whiteside's explanatory notes.) Westfall just didn't give enough context to make the problem clear. I think it is not unreasonable to suggest that Westfall didn't completely understand Newton's mathematics. We are happy to have a sensitive biography; it would be even better to have a biographer who also understood mathematics. But such biographers are rare.
Charles Coulston Gillispie's new biography of Laplace is an expansion of an article which was published in the Dictionary of Scientific Biography in 1978. Robert Fox and Ivor Grattan-Guinness have contributed chapters on Laplace's work in physics and on the history of the "Laplace transform". Princeton University Press has produced an attractive book, with a sturdy binding and an agreeable typeface.
A biography of Laplace is certainly to be welcomed. The 18th century is one of the least-explored periods in the history of mathematics and science. And Laplace by common repute is one of the commanding figures of the mathematics and science of that period. But there is dissent. Clifford Truesdell writes, "Laplace is one of those mathematicians who won a great reputation in his own day and has held it ever since, safe within his forbidding eruption of formalism. The few who have had the courage and industry to follow through some of his teetering calculations have adopted a certain reserve toward him. As a physicist, he preferred contorted structural hypotheses; as a mathematician, he was unusually loose, even for his day; as a teacher, he wrote so as to dazzle rather than enlighten." (The Tragicomical History of Thermodynamics, 1822-1854, Springer, 1980, p. 46.)
Gillispie defines his objectives as follows (p. xi): "The purpose is to give an account of the sequence, range, and results of Laplace's scientific work, explained in terms of his own time and in his own notation. This book does not aspire to be a critical analysis of his mathematical achievements and limitations per se." In terms of these objectives, the book may be said to be a success --depending on what one means by 'explained'.
In contrast to Westfall, Gillispie tells us little about his subject as a person. Laplace's childhood is covered in one paragraph. In one of his few remarks on Laplace's personality, Gillispie writes (p. 67): "We know practically nothing of Laplace's personal life in the years before his marriage, but there are a few indications of his effect on others. Not a single testimonial bespeaking congeniality survives."
The book also draws a rather skimpy picture of scientific life in the 18th century. We learn that there is an institution called the Academy of Science, which elected Laplace to membership, and to which he often read his scientific researches. The events of the French Revolution move Gillispie to give a fuller picture. The Academy is abolished and replaced by the Institute of France. The École Normale, the École Polytechnique and the Bureau of Longitudes are founded. The metric system is devised. Laplace plays a leading role. There is also a very interesting chapter by Robert Fox on the elder Laplace's manipulation of the scientific work of his disciples.
On the whole, though, the book focuses on Laplace's mathematics. The bibliography gives a complete list of his papers; the text itself gives a description of most of them. Unfortunately, these descriptions are usually so superficial that I was unable, in most cases, to get much of an idea of what Laplace was actually doing. "It was in determining the most advantageous factors (given all these complications) that Laplace considered this method to be superior to least squares, and he referred to the general expression that he had given for it in the Third Supplement to Théorie analytique des probabilités:
\( l^{(i)} x + p^{(i)} y + q^{(i)} z + \cdots = a^{(i)}+m^{(i)} \gamma^{(i)}+n^{(i)}\lambda^{(i)} + r^{(i)} \delta^{(i)} + \cdots \)
where \( l \), \( p \), \( q \), \( a \), \( m \), \( n \), and \( r \) are coefficients given by the conditions; \( \gamma \), \( \lambda \), and \( \delta \) are errors in the observations arising from different circumstances, and \( x \), \( y \), and \( z \) are unknowns to be estimated" (p. 255). The equation here is no more than a decoration; in the context, it means nothing.
Gillispie must somewhere have referred to "Laplace's method" for obtaining asymptotic approximations for definite integrals (see, for example, N. G. de Bruijn, Asymptotic Methods in Analysis, North-Holland, 1970; Dover reprint, 1981, Chapter 4). But where? Could it be on p. 89: "Laplace himself had given a method in 'Mémoire sur les probabilités' for converting integrals of differential functions containing factors raised to very high powers into rapidly converging series"? (But the series produced by Laplace's method do not usually converge.) Gillispie's account is just not definite enough to identify this particular mathematical idea in it. (Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 1098, locates the method in the Théorie analytique des probabilités. In less than a page, Kline summarizes the basic idea on which the method rests, and writes out explicitly the result in a typical case.)
Truesdell's remarks might lead the reader to be curious to find out what Gillispie would say about Laplace's mathematical ideas. On p. 12, Gillispie quotes Laplace's definition of probability: "The probability of an event is equal to the sum of each favorable case multiplied by its probability, divided by the sum of the products of each possible case multiplied by its probability...." As it stands, this clearly makes no sense; and the reader will wonder, did Laplace really say that? Is it as nonsensical as it seems, or is there some way to interpret Laplace's words to get a clear meaning? Gillispie does not answer these questions; he only remarks that "the content is standard".
In Chapter 5, we find Laplace deriving the probability distribution for the inclination of the orbit of a comet to the plane of the ecliptic (p. 40): "... perhaps the reasoning is worth following since it exhibits in the most elementary case how Laplace thought about the probability that a certain quantity would be comprised within given limits."
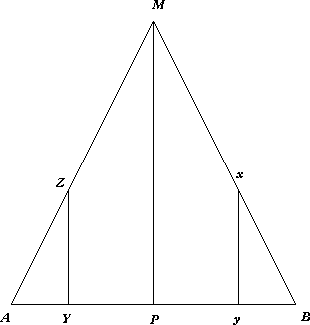
"The line AB = a represents \( 90^{\circ} \), which is the maximum possible mean inclination of the two orbits. On it Laplace constructs a 'curve of probability,' AZMB, along which every ordinate is proportional to the probability that the mean inclination is equal to the corresponding abscissa. Let the mean inclination of the two orbits equal x, where x is less than 1/2a. Then since AY = x and YZ = y, y will be proportional to 2x from A to the midpoint P of AB. Beginning at zero, the value of the inclination of the orbit of comet M may increase by infinitesimal increments dx to a maximum of 2x. Thus YZ = 2AY, and AZM has the form of a straight line and is the hypotenuse of a right triangle APM in which PM = 2AP = a."
In fact, there is no "reasoning" here at all. The whole paragraph is nothing but a bald assertion that the probability curve is a straight line, dressed up to resemble an argument. Gillispie doesn't appear to notice.
Although Gillispie sometimes discusses the relation between Laplace's work and that of other mathematicians --notably Lagrange-- more often he presents Laplace's work as though it were done in isolation. Thus, on pp. 79-81 he discusses Laplace's 1780 attempt to evaluate the integral \( \int_{0}^{1} x^{p} (1-x)^{q} dx \). He does not tell us that this integral is now called a "beta integral" (although on p. 103 he points out that the Lavoisier-Laplace definition of 'specific heat' is not the same as that used by modern physicists), nor does he mention that Euler had evaluated the integral in terms of the gamma function in 1771.
In short, Gillispie's book, though presented as a biography ("A Life in Exact Science"), is little more than an annotated list of Laplace's scientific papers. To some future scholar who wishes to come to grips with Laplace's work, it will be an invaluable road-map. The reader who would like to get some notion of Laplace as a person will be disappointed. So will the mathematician who wants to get an understanding of Laplace's mathematics.
Stacy G. Langton (langton@acusd.edu) is Professor of Mathematics and Computer Science at the University of San Diego. At present, he is at work on a translation of some of the writings of Euler.
The table of contents is not available.
- Log in to post comments




