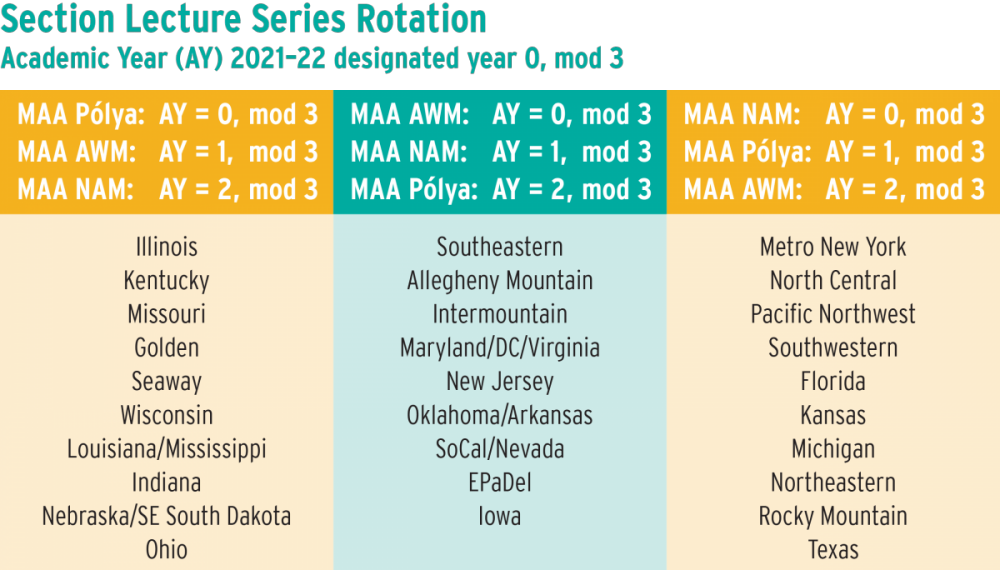
MAA Section Lecturer Series

Harvey Mudd College
Email: [email protected]
Available as a speaker Fall 2020 through Spring 2023

 

Bio: Po-Shen Loh is a social entrepreneur and inventor, working across the spectrum of mathematics, education, and healthcare, all around the world. He is a math professor at Carnegie Mellon University, and the national coach of the USA International Mathematical Olympiad team. He has pioneered innovations ranging from a scalable way to learn challenging math live online at comparable engagement to live-streaming entertainment, to a new way to control pandemics by leveraging self-interest. As an academic, Po-Shen has earned distinctions ranging from an International Mathematical Olympiad silver medal to the United States Presidential Early Career Award for Scientists and Engineers. His scientific research considers a variety of questions that lie at the intersection of combinatorics (the study of discrete systems), probability theory, and computer science. As an educator, he was the coach of Carnegie Mellon University’s math team when it achieved its first-ever #1 rank among all North American universities, and the coach of the USA Math Olympiad team when it achieved its first-ever back-to-back #1-rank victories in 2015 and 2016, and then again in 2018 and 2019. His research and educational outreach takes him to cities across the world, reaching over 10,000 people each year through public lectures and events, and he has featured in or co-created videos totaling over 19 million YouTube views. Po-Shen received his undergraduate degree in mathematics from Caltech in 2004, graduating first in his class. He received a master’s degree in mathematics from the University of Cambridge in 2005, where he was supported by a Winston Churchill Foundation Scholarship. He continued his studies at Princeton, supported by a Hertz Foundation Fellowship and a National Science Foundation Graduate Research Fellowship, where he completed his Ph.D. in mathematics at the end of 2009, and has been on the faculty at Carnegie Mellon University ever since.

Topics include:

Sparking Social Impact By Using Math To Align Incentives
The scale of national and international societal problems can be daunting. One person, or even a small team, are minuscule relative to the number of people who require assistance. There is an area close to mathematics, however, which devises solutions in which problems solve themselves even through self-serving human behavior: Game Theory. The speaker is a pure math professor and researcher who transitioned to using Game Theory to develop new solutions for large-scale real-world problems. He will talk about his experience going from the ivory tower of academia into the practical mess of the real world, where he ultimately innovated fundamentally new approaches to pandemic control (https://novid.org) and advanced math education (https://live.poshenloh.com).
 

 

View the list of past Pólya Lecturers

---

MAA AWM Speakers

     

Karamatou Yacoubou Djima

 

 

 

Bio: Dr. Karamatou Yacoubou Djima is an applied mathematician and an Assistant Professor of Mathematics at Amherst College. Before moving to Amherst, she spent a year at Swarthmore College as a visiting postdoctoral fellow. She received both her Ph.D. and MSc in Applied Mathematics & Statistics and Scientific Computing from the University of Maryland in College Park. Dr. Yacoubou Djima’s current research interests lie at the intersection of applied harmonic analysis and machine learning. Her past and ongoing projects include novel spectral graph methods, early diagnosis of autism spectrum disorder using features present in placenta images, and motion detection in animated images for Pixar.

Topics include:

Heuristic Framework for Multi-Scale Testing of the Multi-Manifold Hypothesis
Global linear models often overestimate the number of parameters required to analyze or efficiently represent datasets, for example when a data set in sampled from a manifold of lower dimension than the ambient space. The manifold hypothesis consists in asking whether data lies on or near a d-dimensional manifold or is sampled from a distribution supported on a manifold. In this talk, we outline a heuristic framework for a hypothesis test suitable for computation and empirical data analysis. We consider two datasets made of multiple manifolds and test our manifold hypothesis on a set of spline-interpolated manifolds constructed based variance-based intrinsic dimensions computed from the data. This is joint work with Patricia Medina, Linda Ness and Melanie Weber.

A brief tour of applied harmonic analysis: from Fourier series to machine learning
I will discuss how the field of Harmonic Analysis has tackled the analysis of data, starting from the year 1807, when Joseph Fourier asserted that all functions can be represented by a trigonometric series, to these days with our obsession with deep learning algorithms. We start by deriving the coefficients in Fourier series and doing so, get some insights into functional analysis, the linear algebra of functions. From there, we establish parallels with the relatively recent field of Harmonic Analysis on graphs and Deep Learning techniques. We will also look at some interesting applications, including analyzing images placenta vascular networks for autism detection.

 

     

Catherine Hsu

 

 

 

Bio: Catherine Hsu is an Assistant Professor in the Department of Mathematics and Statistics at Swarthmore College. Her mathematical interests began as a penchant for logic puzzles and problem solving and grew into a love of abstract algebra and Galois theory while she was an undergraduate student at Rice University. Her research is now primarily in algebraic number theory, including projects related to modular forms and Apollonian circle packings. She also enjoys thinking about mathematical exposition, pedagogy, and unnecessarily complicated strategies for the card game Hanabi.
Prior to joining Swarthmore in the fall of 2020, Hsu was a Heilbronn Research Fellow at the University of Bristol as well as an AAUW American Dissertation Fellow and a Doctoral Research Fellow at the University of Oregon. As a junior researcher, she has greatly enjoyed traveling and speaking at conferences around the world and is looking forward to meeting new mathematicians as part of the MAA-AWM Lecturer program.

Topics include:

Prime Components in Apollonian packings
An Apollonian circle packing is a fractal arrangement formed by repeatedly inscribing circles into the interstices in a Descartes configuration of four mutually tangent circles. The curvatures of the circles in such a packing are often integers, and so it is natural to ask questions about their arithmetic properties. For example, it is known by work of Bourgain-Fuchs that a positive fraction of integers appear as curvatures in any integral Apollonian circle packing. In this talk, we investigate the arithmetic properties of the collection of integers appearing in “thickened prime components'' of Apollonian circle packings.

Projective and Non-Abelian SET
Mathematicians love SET. On the surface, this classic game is a con test of pattern recognition, but it also presents an interesting way to visualize the geometry of a torus over a finite field. In this talk, we will discuss some of the mathematics connected to SET and then explore several new versions of the game, including one arising from projective geometry and one arising from non-abelian groups. In particular, we will see how these non-abelian variations on SET can give intuitive visualizations of abstract group structures.


Small Eisenstein Congruences and Explicit Non-Gorenstein R = T
In his seminal work on modular curves and the Eisenstein ideal, Mazur studied the existence of congruences between certain Eisenstein series and new forms, proving that Eisenstein ideals associated to weight 2 cusp forms of prime level are locally principal. In this talk, we’ll explore generalizations of Mazur’s work to squarefree level, focusing on some work in progress, joint with Preston Wake and Carl Wang-Erickson, that establishes a computable algebraic criterion for having R = T in a certain non-Gorenstein setting.
 

     

Anastasia Chavez

 

 

 

Bio: Anastasia Chavez is an Assistant Professor of Mathematics at Saint Mary’s College of California. Born and raised in California, she transferred from the Santa Rosa Junior College and earned a bachelors in applied mathematics and masters in mathematics from San Francisco State University. After earning her Ph.D. in enumerative and algebraic combinatorics with an emphasis in matroid theory from the University of California, Berkeley, Anastasia was a Huneke Fellow at the Mathematical Sciences Research Institute and Presidents’ Postdoctoral Fellow, NSF Mathematical Sciences Research Postdoctoral Fellow, and Krener Assistant professor at the University of California, Davis.

Topics include:

Matroids, Positroids, and Beyond!
Matroids are a fundamental combinatorial object with connections to many areas of mathematics: algebraic geometry, cluster algebra, coding theory, polytopes, physics ... just to name a few. Introduced in the 1930’s, Whitney defined matroids with the desire to abstract linear and graphical dependence. In fact, every graph is associated with a matroid (called graphical) and from every vector configuration a realizable (sometimes called representable) matroid exists. It has been shown that most matroids are neither graphical or realizable, making these two matroid properties rare and highly desired.
A particularly well-behaved family of representable matroids, called positroids, was introduced by Postnikov and shown to have deep connections to the totally nonnegative Grassmannian and particle physics. Moreover, he described several combinatorial objects in bijection with positroids that compactly ecodes matroidal data and have been shown to characterize many matroidal properties.
With just a few definitions and examples revealing their connections to a variety of fields, you too can begin searching for the matroids living among us.

On the Lattice and Vector Spaces of Cycles of an Undirected Graph
It is well known that cycles in a graph exhibit a rich structure that play a powerful role in many applications. Cycles on graphs, oriented or unoriented, can also lead to deceivingly simple open questions. For example, the Cycle Double Cover Conjecture claims that there is a family of cycles such that every edge of a bridgeless graph is contained in exactly two cycles.
One can consider a linear-algebraic view and consider every cycle as an indicator vector. This translates graphical questions into algebraic ones and leads to structural questions about the cone, lattice, and cycle spaces over some field. This linear algebraic perspective has been applied historically to model combinatorial problems on directed graphs with great success (in some textbooks), whereas the undirected edge case less so. We will explore this algebraic perspective and the distinctions between directed and undirected graphs on the cycle spaces generated by linear combinations of the 0/1-incidence vectors of cycles.

 

     

Marissa Loving

 

 

 

Bio: Marissa Kawehi Loving is an NSF Postdoctoral Research Fellow and Visiting Assistant Professor in the School of Math at Georgia Tech. She graduated with her PhD in mathematics in August 2019 from the University of Illinois at Urbana-Champaign where she was supported by an NSF Graduate Research Fellowship and an Illinois Graduate College Distinguished Fellowship. Marissa was born and raised in Hawai'i where she completed her B.S. in Computer Science and B.A. in Mathematics at the University of Hawai'i at Hilo. She is the first Native Hawaiian woman to earn a PhD in mathematics. Her research interests are in geometry/topology, especially mapping class groups of surfaces (of both finite and infinite type). Marissa is also deeply invested in making the mathematics community a more equitable place. Some of her work includes mentoring undergraduate research (through programs such as [email protected], MSRI-UP, and the Georgia Tech School of Math’s REU) and co-organizing initiatives like SUBgroups and paraDIGMS.

Topics include:

Symmetries of Surfaces
I will give a gentle introduction to surfaces (of both finite and infinite-type) and their associated mapping class groups. I will then discuss some of the different areas of mathematics that naturally arise in the study of surfaces and the mapping class group, from geometry and dynamics to algebra, combinatorics and number theory. Along the way we will see how these different perspectives often come together in beautiful ways.

Surfaces: BIG and small
As a geometric group theorist, my favorite type of manifold is a surface and my favorite way to study surfaces is by considering the mapping class group, which is the collection of symmetries of a surface. In this talk, we will think bigger than your average low-dimensional topologist and consider surfaces of infinite type and their associated “big” mapping class groups.

Where do I belong? Creating space in the math community
Who belongs in mathematics? Who is given the resources they need to flourish mathematically? Who is undermined, sidelined, and excluded by both their peers and seniors? I will address these questions from the perspective of my own personal mathematical journey. I will also share some of the programs and spaces I have helped create in my quest to make the mathematics community into a place where folks from historically underrepresented groups (particularly women of color) can feel safe, seen, and free to devote their energy to their work. If you have ever felt like you don’t belong or worried that you have made others feel that way, this talk is for you.

 

 

     

Recently Added: Emilie Purvine

 

 

 

Bio: Dr. Emilie Purvine is a mathematician and data scientist at Pacific Northwest National Laboratory. She joined PNNL in 2011 after receiving her PhD in mathematics from Rutgers University with a focus on enumerative combinatorics and nonlinear recurrence relations. While at PNNL Emilie has had the opportunity to contribute to a variety of projects tackling hard problems in applications including computational biology and chemistry, power grid modeling, cyber network analysis, and knowledge models. Her current mathematical research focus is on topological data analysis applied to discrete structures like graphs and hypergraphs. Much of her work involves finding mathematical nuggets in applied domains and working on theoretical advances to enable operational progress.

Emilie also greatly values the ability to make mentoring a focus of her work. She loves to give presentations to students at all levels to provide an example of what a mathematician can do outside of academia. Interns and postgraduates (2-3 year temporary employees including post bachelors, post masters, and postdoc) are always included into her projects to promote on the job learning.

Outside of her core work activities Emilie has also been the chair of the MAA’s Membership Committee and an associate editor of the AMS Notices. In her free time Emilie spends time with her friends and family, enjoys a good book, loves the outdoors and traveling to new destinations.

Topics Include:

Mathematics for Cyber Security
The security of computer networks is crucial to maintain data privacy, intellectual property rights, and even to keep infrastructure functioning reliably. One might think that cyber security is the responsibility of computer scientists and network administrators. This is certainly true, but as adversaries change their tactics and become increasingly sophisticated, mathematicians are lending a hand. In this talk I will begin by introducing the landscape of computer networks, the cyber kill chain, and cyber security operations. I will present some of the main challenges facing cyber security today and show how mathematicians, like myself, are applying their skills in data modeling, anomaly detection, and machine learning to help provide situational awareness and keep computer networks resilient.

Graphs and Hypergraphs and Topology, Oh My!
Mathematical structures and concepts can be great models of real-world data. For example, differential equations have a long history of success in applied mathematics to model dynamics found in rivers and oceans, the atmosphere, and molecular systems (just to name a few!). Network science is an area of applied math that uses graph structures to model relational systems like social, collaboration, and transportation networks. Graphs, however, are limited to modeling pairwise relationships among entities. Hypergraphs and topological spaces provide alternate models of relational systems that allow for arbitrary sized and structured relationships. In this talk I will introduce the mathematical concepts of graphs, hypergraphs, and topology and show how they are used to model real-world data from a variety of applications including biological systems, chemistry measurements, and cyber networks. We’ll also talk about what measurements and properties of these structures can tell us about the systems they model.

 

     

Recently Added: Karen Lange

 

 

 

Bio: Karen Lange is the Theresa Mall Mullarkey Associate Professor of Mathematics at Wellesley College. In her research, she studies the "balance scales" used to calibrate computational information and applies these tools to measure the difficulty of algebraic problems. She's also passionate about community-building and inclusion in mathematics, and she teaches a seminar on writing about mathematics for the public. She earned her undergraduate degree at Swarthmore College and her doctoral degree at the University of Chicago, and she completed an NSF Postdoctoral Fellowship at the University of Notre Dame.

Topics Include:

Different Problems, Common Threads: Computing the difficulty of mathematical problems
Mathematics is filled with theorems that state the existence of a desired object. For example, a result known as Weak Kőnig's Lemma (which I'll introduce) states that "every binary tree with infinitely many nodes has an infinite path". But just because we know an object exists, doesn't mean we can find it. Given Weak Kőnig's Lemma, it's natural to ask whether we can compute a path through a given binary tree with infinitely many nodes. It turns out the answer to this "Path Problem" is "no", so we say that the problem is not "computable". But then just what exactly is the computational power of this Path Problem?
Using this Path Problem as a test case, we will explore the key ideas behind taking a "computable" perspective on mathematics (over an "existence" one) and describe an approach for measuring the computational power of mathematical problems. We'll see that the computational power of problems varies widely and studying problems' power helps to illuminate what really makes problems "tick".

Classification via lists in computable structure theory
"Classifying” a natural class of structures is a common goal in mathematics. Providing a classification can mean different things, e.g., determining a set of invariants that settle the isomorphism problem or instead creating a list of all structures of a given kind without repetition of isomorphism type. Here we’ll discuss classifications of computable structures of the latter kind and provide a self-contained introduction to computable structure theory along the way. We’ll consider natural classes of computable structures such as vector spaces, equivalence relations, algebraic fields, and trees to better understand the nuances of classification via effective lists and its relationship to other forms of effective classification.

---

MAA NAM Speakers

     

Lorin Crawford

 

 

 

Bio: Lorin Crawford is a Senior Researcher at Microsoft Research New England. He also holds a position as the RGSS Assistant Professor of Biostatistics at Brown University. His scientific research interests involve the development of novel and efficient computational methodologies to address complex problems in statistical genetics, cancer pharmacology, and radiomics (e.g., cancer imaging). Dr. Crawford has an extensive background in modeling massive data sets of high-throughput molecular information as it pertains to functional genomics and cellular-based biological processes. His most recent work has earned him a place on Forbes 30 Under 30 list, The Root 100 Most Influential African Americans list, and recognition as an Alfred P. Sloan Research Fellow and a David & Lucile Packard Foundation Fellowship for Science and Engineering. Before joining Brown, Dr. Crawford received his PhD from the Department of Statistical Science at Duke University and received his Bachelor of Science degree in Mathematics from Clark Atlanta University.

Topics include:

Interpretability in Black Box Statistical Methods
A consistent theme of my work is to take modern statistical and machine learning approaches and develop theory that enable their interpretations to be related back to classical principles in biology. The central aim of this talk is to address variable selection questions in “black box” nonlinear and nonparametric regression. Motivated by statistical genetics, where nonlinear interactions are of particular interest, we will introduce novel, interpretable, and computationally efficient ways to summarize the relative importance of predictor variables. These approaches both (1) capture nonlinear structure of data and (2) provide significance measures for powerful variable selection.

Variable Selection with 3D Shapes
The recent curation of large-scale databases with 3D surface scans of shapes has motivated the development of tools that better detect global-patterns in morphological variation. Studies which focus on identifying differences between shapes have been limited to simple pairwise comparisons and rely on pre-specified landmarks (that are often known). In this talk, we present statistical pipelines for analyzing collections of shapes without requiring any correspondences. Our method takes in two classes of shapes and highlights the physical features that best describe the variation between them.

 

     

Haydee Lindo

 

 

 

Bio: Dr. Haydee Lindo is an assistant professor of mathematics at Harvey Mudd College. Dr. Lindo is from Jamaica and earned her BAs in mathematics and political science. She received her Ph.D. in mathematics from the University of Utah and was previously a Gaius Charles Bolin Fellow and, later, an assistant professor of mathematics & statistics at Williams College. Dr. Lindo is a commutative algebraist with research interests in homological algebra and representation theory. She focuses on the development and application of the theory of trace modules over commutative rings.

Topics Include:

Introduction to trace ideals and centers of endomorphism rings
In many branches of mathematics, the full set of "functions" between two objects exhibits remarkable structure; it often forms a group and in some special cases it forms a ring. In this talk, we will discuss this phenomenon in Commutative Algebra. In particular, we will talk about the endomorphism ring formed by the homomorphisms from a module to itself by first looking at commuting square matrices with real entries. The well-known trace map on matrices can be generalized to a map on any module over a commutative ring. The image of such a map is a trace ideal. I'll introduce the trace ideal and explain its role in the question "What properties of a module does its endomorphism ring detect?"

Stable Trace Ideals and Arf Rings
In this talk we will explore the intersection of notions of an ideal being “trace” and an ideal being “stable” that is, ideals that map to themselves under all homomorphisms to the base ring and ideals that isomorphic to their endomorphism rings. Following Lipman’s seminal work exploiting the nice properties of stable ideals to study Arf rings, we apply our results, incorporating the modern theory of trace ideals, to show that Arf rings enjoy even more geometric and homological properties than previously known. This is joint work with Dr. Hailong Dao.

 

     

Jose Perea

 

 

 

Bio: Jose Perea holds a Ph.D. in Mathematics from Stanford University (2011) and a B.Sc. in Mathematics from Universidad del Valle, Colombia (Summa cum laude and Valedictorian, 2006). He was a visiting assistant professor in the department of Mathematics at Duke University from 2011 to 2015, and a member of the Institute for Mathematics and its Applications (IMA) at the University of Minnesota during the Fall of 2014. In August of 2015 he joined Michigan State University as an Assistant Professor with joint appointments in the department of Computational Mathematics, Science & Engineering (CMSE), and the department of Mathematics. He is the recipient of a 2020 NSF CAREER award, a 2020 honoree of Lathisms during Hispanic heritage month, a 2018 honoree of Mathematically Gifted and Black during black history month, and recognized as being in the top 5% of teachers at Duke University (2013).

Topics Include:

The Underlying Topology of Data
Topology, and particularly algebraic topology, seeks to develop computable invariants to quantify the shape of abstract spaces. This talk will be about how such invariants can be used to analyze scientific data sets, in tasks like time series analysis, semi-supervised learning and dimensionality reduction. I will use several examples to illustrate real applications of these ideas.

DREiMac: Dimensionality Reduction with Eilenberg-MacLane Coordinates
Dimensionality reduction is the machine learning problem of taking a data set whose elements are described with potentially many features (e.g., the pixels in an image), and computing representations which are as economical as possible (i.e., with few coordinates). In this talk, I will present a framework to leverage the topological structure of data (measured via persistent cohomology) and construct low dimensional coordinates in (classifying) spaces consistent with the underlying data topology.

 

     

Talea Mayo

 

 

 

Bio: Talea Mayo is a computational mathematician with expertise in the development and application of numerical hydrodynamic models for coastal hazards. She specializes in hurricane storm surge modeling, including their use for the investigation of climate change impacts on coastal flood risk. She also has expertise in statistical data assimilation methods for state and parameter estimation. She has recently expanded her work to include coastal erosion and the impacts of sustainable resilience efforts. She earned her B.S. in Mathematics from Grambling State University, and her M.S. and Ph.D. in Computational and Applied Mathematics from The University of Texas at Austin. She is currently an Assistant Professor in the Department of Mathematics at Emory University, and was recently awarded the Early-Career Research Fellowship by the National Academies of Sciences Gulf Research Program and the Early Career Faculty Innovator Award by the National Center for Atmospheric Research. She is a fierce advocate of accessible, inclusive science and education of all people, and spends her free time chasing marathon PRs and toddlers.

Topics include:

Mathematics applied: the use of computational models to understand climate change impacts to storm surge risk
It is widely accepted that climate change will cause global mean sea level rise, increasing coastal flood risk in many places. However, climate change also has significant implications for tropical cyclone climatology. Specifically, hurricane intensity, size, and translation speed are all expected to intensify in the future, and each of these influences storm surge generation and propagation. In this talk, I will discuss probabilistic and deterministic numerical modeling approaches we have taken to understanding what this means for coastal flooding from storm surges.

Data meets model: how observations are used to improve prediction and simulation of hurricane storm surges
Coastal ocean models are used for a variety of applications, including simulation of tides and hurricane storm surges. These models numerically solve the shallow water equations, which assume large horizontal length scales relative to the vertical length scales, and allow depth integration of the Navier-Stokes equations. The inherent uncertainties in coastal ocean models are a result of many factors, including this modeling assumption, numerical discretization of the resulting equations, and uncertain model inputs and parameters. In this talk, I will discuss how we have used statistical data assimilation methods for state and parameter estimation to quantify and reduce model uncertainties.

Theories of evolution: how my research program and I have transformed through my career in academia
I began my career as a criminal justice student in hopes of becoming a lawyer, but when I realized I had already fulfilled all the math requirements, I quickly changed my major to mathematics. Mathematics provided the foundation for me to participate in multiple interdisciplinary summer research opportunities, and living in Louisiana during Hurricane Katrina solidified my interest in using math as a tool for solving real world problems. I chose an interdisciplinary program for my graduate studies, and gained expertise in numerical storm surge modeling. Upon earning my PhD, I learned to use storm surge models for coastal engineering and climate change applications as a postdoctoral researcher. I expanded my research program to include wave energy and coastal erosion when I became a tenure track faculty member. In this talk, I’ll discuss my research program, my path to becoming part of the 1% of faculty who are black women, and my efforts to improve this statistic through outreach and education.

 

     

Recently Added: Candice R. Price

 

 

 

Bio: My name is Candice Price, and I am currently an associate professor in the department of Mathematics at Smith College in Northampton MA. I was born and raised in California and earned a bachelor’s degree (2003) from California State University, Chico, and a master's degree (2007) from San Francisco State University, both in mathematics. I earned my doctoral degree (2012) in mathematics from the University of Iowa under the advisement of Isabel Darcy. My area of research is applied mathematics, with an emphasis on mathematical models for biological questions. I also have research interests in math education and problems in the intersection of mathematics and social justice. In my teaching, research, and service, I focus on a collaborative approach and view my work through the lens of inclusion and diversity.

Topics Include:

Can we make grace the norm in our classrooms?
For much of my life, I was always confused about the way that people perceived the relationship between students and instructors in the classroom, especially in mathematics. There is such an adversarial relationship that even sharing my career choice with strangers leads to groans and stories of trauma. I believe this is what happens in a classroom without grace. So when we add grace the opposite should happen, right? During our time together, I hope to discuss with you the ways that I incorporate grace in my classroom and why many people think it is radical. I invite everyone to come and reflect on ways they can make grace the norm in their classrooms and spaces.

Using Mathematics to Unlock Biological Mysteries
Mathematical modeling is an effective resource for biologists-- it provides ways to simplify, study and understand the complex systems common in biology and biochemistry. Many mathematical tools can be applied to biological problems, some traditional and some more novel, all innovative. This presentation will review some of the mathematical tools that I use to study biological questions including knot theory applied to DNA-protein interactions and using social networks to study evolutionary success.

Viewing the World through a Mathematical Lens
The way that numbers interact within the world has fascinated me from an early age. My research path has lead me to work on problems that are essentially about viewing the world through a mathematical lens. While discussing my journey to a career in Mathematics, I will share with you some of my favorite mathematical applications, including but not limited to DNA knotting, fighting parasites and Gerrymandering organs.

 

Recently Added: Opel Jones

Biography and Topics to come.

---

Questions about Section Lecturers? | email MAA Communities at [email protected]