By Lew Ludwig

An Administrator’s Quip
“If they want to ruin their education, that is up to them. We can’t stop them.” Someone recently shared this remark from an administrator who was responding to a question about whether they were concerned about what AI is doing to student learning. The exact circumstances and preceding exchange that led to the comment are unclear, but the message was not—it’s on them. This sort of nonchalant cop-out reminded me of the faculty member who does not take attendance because “they’re adults.” As if there is some switch that flips when a person turns 18, suddenly granting the ability to make the right decisions when faced with hard choices. At this stage in my career, I find these types of students few and far between.
The Broken Supply Chain
Dr. Tricia Bertram Gallant, co-author of The Opposite of Cheating, describes what she calls the Moral Obligation Supply Chain, a concept that, in this case, snapped at the institutional link. Instructors have the duty to design pedagogy and assessments that invite honesty—work that rewards understanding rather than shortcuts. When we do that well, students can meet us in kind, demonstrating their learning fairly and honestly. Their integrity, in turn, allows us to assess their work with the same fairness and honesty we hope to model. But when institutional leaders shrug and say, “It’s on them,” they break the final link in that chain—the institution’s moral obligation to uphold and certify genuine learning.
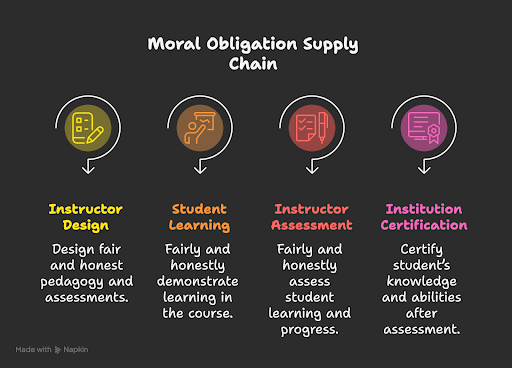
Degrees are not personal property but collective goods, much like currency. When institutions take the “it’s on them” approach and graduate underprepared students, employers lose trust in that institution and devalue all of its degrees, harming the very students who upheld their end of the moral obligation.
The False Comfort of "We Can't Stop Them"
As we approach the third anniversary of ChatGPT’s release, it is clear that “catching” students is a losing game, a point underscored by the recent TEQSA report from Australia. AI detectors have an unreliably high false positive rate, lock down browsers can be circumvented with VPNs, and planting trojan horse traps in assignments hardly qualifies as fair or honest assessment. But just because detection is difficult does not mean we can abdicate responsibility.
Learning from Australia: Strategic Adaptation, Not Surrender
Australia’s national higher education regulator, the Tertiary Education Quality and Standards Agency (TEQSA), recently released a report on generative AI and academic integrity. The report emphasizes that maintaining integrity in learning is a shared responsibility among students, faculty, and institutions. It urges universities to redesign assessments so they are resilient to AI misuse by shifting toward more authentic, multimodal, and scaffolded work such as portfolios, oral defenses, and project-based assignments. It also recommends “two-lane” assessment design: secure, proctored assessments that ensure core learning outcomes alongside open tasks where AI is permitted but used transparently and purposefully.
What Math Instructors Can Do Now
While institutions debate large-scale reforms, we can begin modeling the spirit of those recommendations in our own classrooms. Here are a few examples of what I call harm reduction for assessment. They are not perfect solutions, but they can help prepare us—and our students—for the larger conversations ahead.
1. In-class problem lottery from homework
Suppose homework included ten problems on limits. At the start of class, draw one “lottery” problem. Students get 5–10 minutes to solve it on paper or in groups. This encourages them to do the homework rather than copy it, since any question might appear live.
Bonus: Have them briefly explain their reasoning aloud or annotate what they changed from their original attempt.
2. Reflection Prompts with Homework
Add a one-sentence metacognitive question to each assignment—something AI can’t answer meaningfully.
Examples:
- “Where did you second-guess yourself on this problem?”
- “If you could ask a hint-giving version of me one question before solving this, what would it be?”
- “Describe one common mistake a classmate might make here.
These short reflections take a minute to write but reveal whether students actually engaged with the material.
3. Decision-Making Under Uncertainty
Lean into the technology rather than trying to wall it off. Ask students to use AI as an advisor, not an oracle. Have them prompt the model for two or more distinct strategies for solving a calculus problem, then evaluate which approach they would trust and why.
Example:
Ask Gemini or ChatGPT to propose multiple ways to find the volume of the solid formed by rotating y=ln(x)y = \ln(x)y=ln(x) about the x-axis on [1, 3]. Compare the methods—disk, shell, or numerical integration—and decide which you would use, explaining your reasoning and any trade-offs.
Even when AI produces perfect solutions, students must analyze efficiency, interpret assumptions, and justify decisions. These are the core habits of mathematical judgment that cannot be automated.
Protecting the Honest Students
So let us return to that administrator’s quip: “If they want to ruin their education, that is up to them.” This is not only wrong but harmful. When institutions abandon their gatekeeping role, they do not merely fail the students who cut corners. They fail every student who stayed up late wrestling with a concept, who sought help during office hours, who earned their degree honestly. These are the students who trusted that their hard work would be valued and certified by an institution worthy of that trust. The Moral Obligation Supply Chain only functions when all links hold firm.
We cannot control whether every student chooses to learn, but we can control whether we design assessments that invite learning and whether our institutions uphold the value of the degrees we confer. The choice before us is not between stopping AI or surrendering to it; it is between strategic adaptation and defeatist abdication. And for the sake of every honest student who believes their degree means something, we must find the courage to do what is right, not merely what is easy. In the words of Gandalf, even in the shadow of great change, "all we have to decide is what to do with the time that is given to us." The time is now. The choice is ours.
AI Disclosure: This column was shaped with the help of ChatGPT (GPT-5) and Claude (Opus 4.1), which I used as a sounding board to refine transitions and test phrasing. The story, arguments, and voice remain fully my own, just assisted, as always, by a bit of digital fellowship.

Lew Ludwig is a professor of mathematics and the Director of the Center for Learning and Teaching at Denison University. An active member of the MAA, he recently served on the project team for the MAA Instructional Practices Guide and was the creator and senior editor of the MAA’s former Teaching Tidbits blog.
