By Pup Horst
A magician searches for community
Joe Ledoux is “not” a “mathematician” – he is an artist and a magician. However, he joins the likes of Marjorie Rice and an anonymous internet forum user in crafting new mathematics as inspired by his main interests. He made a new visualization of the hypercube that does not distort its constituent cubes.
Ledoux named his discovery the “Hyperdoors Theory”. The mathematician Tom Banchoff, who once worked with Salvador Dalí on hypercube visualization, certified that the hyperdoors theory is a “mathematically sound, clever way to view a four-dimensional object.”
After his conversations with Banchoff, Ledoux is eager to continue discussing his model with other mathematicians. As Ledoux puts it, “These are the things I want to sit and have coffee chatting about – but I’ve found that the fourth dimension is a lonely place.” We’re here to help him find people to chat with who are also interested in these ideas!
A projection of the hypercube
Consider the following image of a cube:
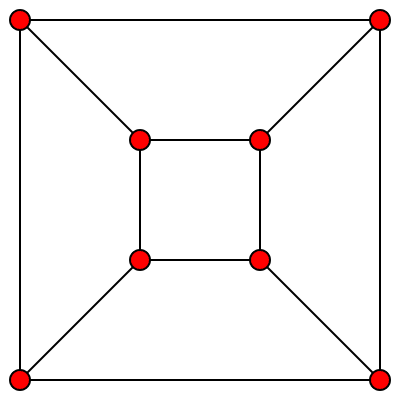
Kind of doesn’t look like a cube, does it? But if you allow yourself to perceive depth in the image, to see the inner square as farther away than the outer square, you can start to see how this really is a visualization of a cube.
A cube has six sides; each side is a square. But in the above image, we see one square surrounded by four trapezoids, and the outer edges of those trapezoids form a second, larger square. The six squares of the cube appear distorted in this two-dimensional image.
Here is a picture of a three-dimensional projection of the hypercube:

We see an inner cube surrounded by six frusta, and the outer faces of these frusta form another cube. In actuality, the hypercube is formed from eight cubes. Here is a net of the hypercube folding up into the projection we saw:
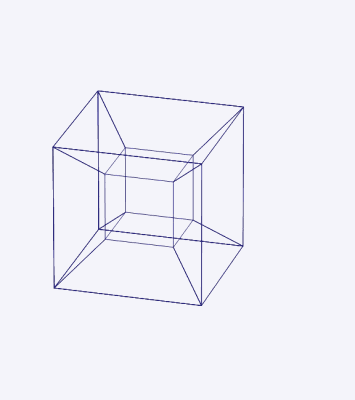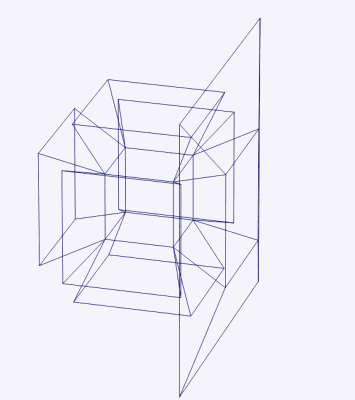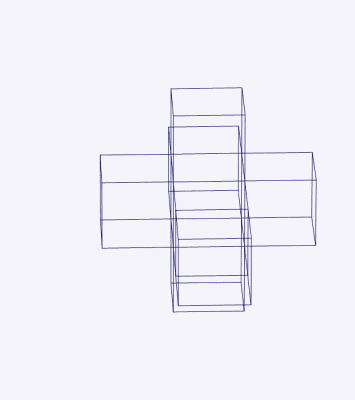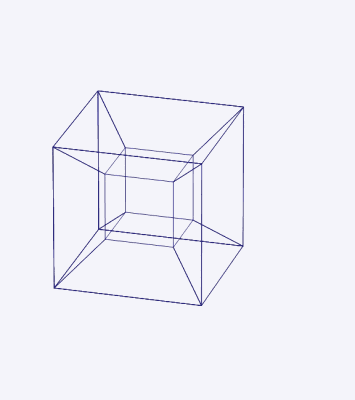
Properly speaking, this folding does not happen in three-dimensional space and does not require any of the cubes to change their shape. Rather, the net folds into four-dimensional space and the cubes join together at their faces to form the cells of the hypercube. This is analogous to the six squares of a cube’s net: the squares fold up into three-dimensional space without changing their shape and join together at their edges to form the faces of the cube.
We can look at a cube and see it with its six square sides undistorted. We can even look at a two-dimensional projection of the cube, intuit depth, and recognize its true, undistorted geometry. Unfortunately, when we look at three-dimensional projections of the hypercube, we cannot intuit “depth” in the four-dimensional sense, and we cannot easily grasp its true, undistorted geometry.
According to Ledoux, the mathematician Richard J. Gran told him that it would be impossible to visualize a hypercube without distortions. This sparked Ledoux’s interest and inspired him to join a long tradition of artists reaching into four-dimensional space to further their art and instill beauty and mystery into the world.
The Hyperdoors Theory
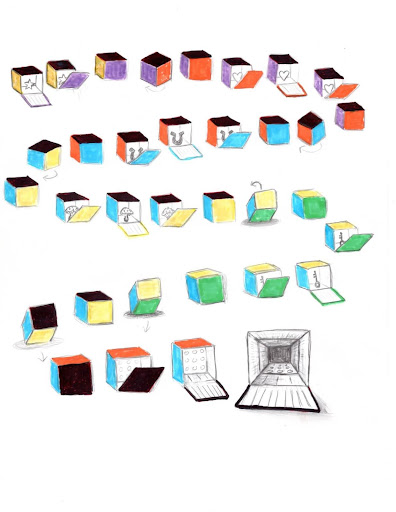
In a fancy art museum, there is a magician adorned with a cape and a top hat. He stands upon a stage before an enthralled audience – they are about to witness real magic. He shows them a simple box with a door in front, one of the eponymous hyperdoors.
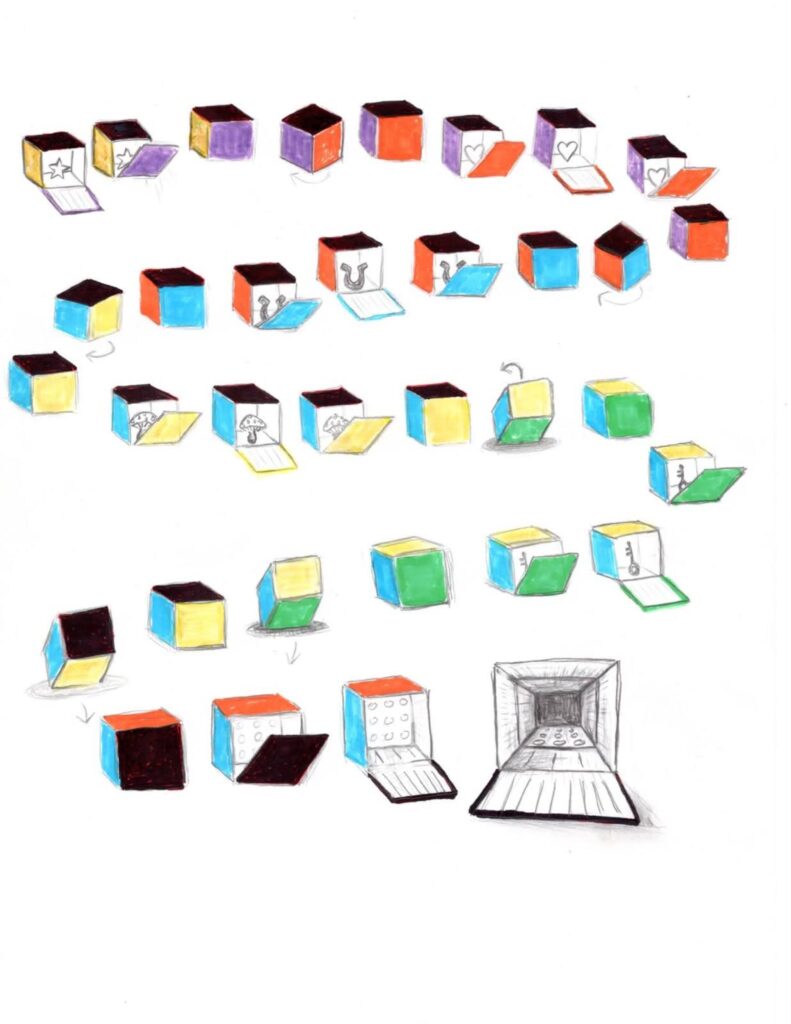
The door opens and the audience sees into the cube. Geometrically, everything looks exactly as they would expect, with the addition of a star sitting in the box. The door closes, and the magician rotates the cube. Now the audience sees a second door, and it too opens. Once again, everything about the geometry inside the cube looks exactly as they would expect, but this time the star is magically replaced with a heart!
This process continues several more times, each time with a new object inside the box: a mushroom, a horseshoe, a key, and then finally the sixth door opens to reveal no object at all. Instead, the sixth door shows the audience a seventh door in the back – when this door opens, they see into another cube, the exact size as the one he’s been showing them this entire time.
Their gasps give way to thunderous applause – how else could they respond to witnessing real magic? To Ledoux, real magic is simply magic that is precisely what it purports to be, rather than using a gimmicked object. Real magic is magical precisely because it can be fully explained.
In this case, the box the magician held was in fact a projection of a hypercube. Unlike what we saw before, the cubes in this visualization are not distorted at all. The cube the magician holds is the outer cube of the projection above. Opening each of the six doors allows us to look inside an adjacent cell of the hypercube – what was before distorted into a frustum – but this time the cell remains in its original cubic shape.
The various objects inside help us recognize that we are in fact seeing into different cells of a hypercube and that each of these cells are non-distorted cubes. Moreover, the simple rotations allow us to remember that the cubes adhere together perpendicularly to form the hypercube. This visualization affords us a new avenue for intuiting the basic geometry of the hypercube, all while enjoying quite the magic show!

Artist, Magician, Mathematician
Currently, the only tangible visualization of the hyperdoor theory is the image you saw above. Ledoux deeply desires to make an animation of the hyperdoors. He knows that some mathematicians are quite skilled with mathematical animations, and he would love to work with someone to make the hyperdoors as visually intuitive as possible.
If you are interested in collaborating with Ledoux on creating an animation of the hyperdoors or furthering their mathematical framework, please reach out to him. Even if all you want to do is chat with him, please contact him! My conversations with him have been very illuminating – his view of higher-dimensional geometry and mathematics in general is quite inspiring.
Ledoux thinks people are often separated into different domains, be it scientific or artistic or spiritual. To him, there’s something very hopeful about being able to perceive four-dimensional space, as it requires us to blend together those different domains and see beyond our immediate reality.
As a magician, Ledoux thinks of mathematics as being very magical. He considers that mathematical truths allude to something deeper in the world. For him, that “something” is spiritual. Whether or not any given individual agrees with that literal stance, I think most mathematicians agree that mathematical truth has a deep, intrinsic beauty to it.
When I first spoke with Joe Ledoux, he told me that “[I’m] a real magician.” After getting to know him while collaborating to write this post, I am quite comfortable proclaiming: Joe, you’re a real mathematician!

Pup Horst is currently faculty at Case Western Reserve University and the deputy editor of MAA Math Values. While xyr work was originally in lower-dimensional higher category theory, these days xe focuses primarily on pedagogy and teaching. In addition to finding xem dancing xyr way through math classes, you can find xem working with xyr cohort of Posse scholars, a group of diverse, leadership students on campus xe mentors as part of xyr role as Posse Faculty Mentor.