By Dave Kung
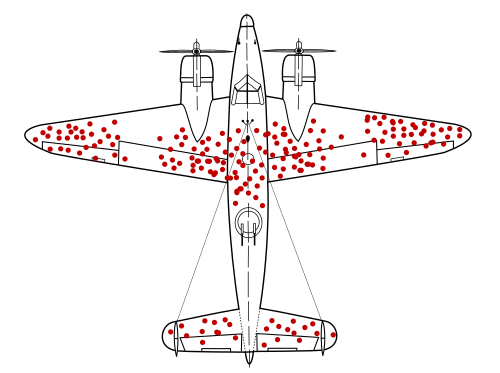
When mathematician Jordan Ellenberg wanted to demonstrate to the general public How to Not Be Wrong – how mathematics can help us be more precise and successful in our thinking – he started with the story behind this famous image. When planes returned from World War II firefights, the bullet holes (in red) weren’t evenly distributed. Reinforcing the planes was expensive (both in weight and money); doing so optimally was vital. Which parts of the planes should be reinforced? The key insight is that researchers were only seeing the planes that didn’t get shot down. The planes hit by bullets in the areas without red dots never made it back. Those were the areas that needed more protection.
Only seeing what’s in front of you (a form of survivor bias), without a thought about what you’re not seeing, leads to both incredibly natural and deeply flawed thinking. In many cases, this sort of flawed reasoning keeps us in the mathematical sciences from better serving students.
Let me explain with a few examples.
Like many people who successfully navigated the US higher education system and got an advanced degree, I started college full-time at a 4-year institution. Chances are pretty good that you did too – when I ask higher ed math audiences, typically over 80% attended a single undergraduate institution. Who are we not seeing? Every year there are about 5 million students in the community college system – just under 40% of the college-going population (according to NSC data). Even though 80% of those who start community college full-time intend to transfer and earn a bachelor’s degree, only about 16% earn that degree within six years according to CCRC data. (That rate is 62% for students starting at a 4-year institution.) Success rates are even lower for Black and Latinx community college students and those experiencing poverty – groups that disproportionately start in the 2-year college system.
What would it take to improve those numbers – to strategically reinforce those parts of our metaphorical planes? Some causes are beyond the control of the mathematics community (e.g., poverty, family caretaking obligations). But others are well within our sphere of influence: transparent and sensible transfer policies, degree requirements aligned with student interests, and state-wide coordination across institutions and systems. These and other recommendations are laid out in Just Equations’ excellent new report, A Complex Equation: Confronting Math Obstacles on the Transfer Path and were discussed at a recent Just Equations / TPSE Math webinar.
Calculus is still a vital subject for most STEM, economics, and business majors. It’s a course I’ve taught at least a dozen times, and like most professors, I always worked hard to support the students sitting in my class. But who are we not seeing? Too many students – many of whom are eager to pursue STEM degrees – are caught in the trap of developmental mathematics. Like the planes that took fire in their engines, they require more mental work to see. Yes, an increasing number of those students have gaps in their mathematical backgrounds, but the evidence is clear: putting them in remedial classes is not the answer. The traditional sequence of College Algebra / Trigonometry / PreCalculus serves very few students well.
What would it look like to reinforce those parts of our system? STEM-intending students currently placed into those courses would be far more likely to pass calculus if placed directly into calculus, with a corequisite support course if needed. As David Bressoud noted in his MathValues column unpacking this research, the best preparation for calculus is calculus. Reforming our placement practices to get more students into more advanced courses – making sure that students with no interest in STEM or economics are taking the Statistics or Quantitative Reasoning course that fulfills their mathematical needs – would improve outcomes for nearly everyone. Despite the perception of some faculty (explained brilliantly here), evidence shows that such efforts (including mandated ones in California) do indeed improve success rates.
What about math majors, the ~1% of students who choose to study our beloved subject more deeply? Who are we not seeing when we look at them? The story I hear regularly is that most departments start the vast majority of their majors in second or third semester Calculus – if not Linear Algebra. Having taken high school Calculus is almost a foregone conclusion.
Most faculty’s closest direct connection to our K12 system is through their own kids, who either take high school calculus or choose not too. Most are surprised to learn how many American public high school schools don’t even offer the course. Access is high at schools that serve a primarily White (76%) or well-off students (87%). Other schools are far less likely to offer Calculus, including those serving primarily students of color (52%) and those with substantial low-income populations (45%).
If we believe that “mathematical potential is distributed equally among different groups, irrespective of geographic, demographic, and economic boundaries,” as Federico Ardila describes it in his first axiom, then many of our math majors should be starting college in first semester Calculus - or even below that. Moving in that direction is less of a policy change and more of a cultural one. It requires all of us questioning our sub-conscious assumptions – based in part on survivor bias – about where to find students with high mathematics potential. Encouraging successful students in all of our classes to take more mathematics isn’t difficult, but it does require intentionality and a change in perspective.
When the pattern of bullet holes in planes was observed by the military, they were inclined to reinforce the parts of the planes with the most damage. It was only when Abraham Wald and the Columbia Statistics Research Group took a critical, unbiased look at the data that they were able to reverse this decision, improving the odds that planes made it home safely. We in the mathematics community are in a similar position. We spend most of our time and energy with the students who have survived. If we apply the mathematical thinking Ellenburg claims is core to our field, we will take a critical, unbiased look at the data and make decisions that will improve the odds that more students – including the ones we currently don’t see so easily – will succeed.
What are you doing to better support students – especially ones it’s harder to see? Come join the conversation on MAA Connect.
Note: The true story of Wald and the SRG group is undoubtedly more complicated than the myth I am amplifying in this piece. For more, Bill Cassleman has written a detailed Notices article that includes a post-script with additional information and references.

Dr. Dave Kung has worked in the intersection of mathematics and equity for three decades. He served as the Director of Policy at the Charles A. Dana Center at The University of Texas at Austin, and as Director of MAA Project NExT. He also works closely with K-12 and higher ed organizations, especially concentrating on equity issues in mathematics. Kung was awarded the Deborah and Franklin Tepper Haimo Award, the MAA’s highest award in college math teaching, for his work at St. Mary’s College of Maryland. He resides there, serving as Executive Director of Transforming Post-Secondary Education in Mathematics (TPSE Math) and working as an independent consultant, as well as playing violin and running–never simultaneously, but sometimes alongside his partner and daughter. The views expressed in this column are Dave’s alone and do not represent those of any organizations he works with or for.