By Keith Devlin @KeithDevlin@fediscience.org, @profkeithdevlin.bsky.social
Sometime in the early 2000s, my primary care physician offered me the option of no longer having an annual health checkup in person. Rather, I could just call into my nearest walk-in testing lab and have a blood draw, followed up a few days later by a quick video-chat. (They also wanted me to take my blood pressure and submit the results online; as a moderately serious endurance athlete, I was tracking my BP anyway.) Only if the blood panel showed any unusual results would they (possibly) call me in for an in-person examination.
The point was, they said, that these days a relatively few samples of blood (three or four vials, as I recall) were enough to give a reliable picture of how I was doing. Though the body has a large number of moving parts that are inter-related in complex ways, it was all assembled from a few essentially similar components (at some level of stratification).
Having just completed my 2001 book The Math Gene, where I presented a rational reconstruction of how the human brain likely acquired the ability to do mathematics, I was immediately struck by the idea of finding a “blood panel” for mathematical ability. Could the skillset to handle the wide ranging curriculum for K-12 mathematics education be reduced to mastery of a small number of key activities that:
- If mastered, would result in an ability to solve any problem in the domain of the curriculum (in the sense that the individual could, on their own, acquire and master any specific unfamiliar skills required to solve it;
- If the individual were assessed on their mastery of the “blood panel” activities, a reliable inference could be made as to their overall mathematical ability?
We professional mathematicians provide an existence proof that such is possible in the case of goal 1. There comes a point in our development where we get to that level of mastery, some of us fairly quickly, others requiring a bit longer.
It took a while, and I was not working alone, but the answer was “Yes” for goal 1 and “Maybe” for goal 2. The suite of activities we developed (funded in part by a substantial award of $1.1M for two years from the US Department of Education) was released as a Web application in 2018. We didn’t make a big announcement, since the relatively small efficacy studies that were conducted for the Department of Education by the large nonprofit educational research organization WestEd, would need to be followed up by much larger studies before we could make any confident claims. And some additional small-scale studies were required before we did that, likely resulting in further work on the suite. But the results WestEd did obtain were suggestive that we were on the right track (rather, an effective track).
Last year we were finally ready to work with WestEd on a proposal to conduct that necessary large scale study, starting in 2025. Only to be faced, early in the year, with the reality that the very federal organization that would (if funded – though WestEd has a good track record in securing federal grants) support the project no longer existed. The Department of Education was one of many casualties of a shift in the winds of what the American voter was willing to support in terms of education research and science and technology R&D. So, as of now that study is on ice (most of the funds saved by many such cancellations having instead been funneled to support an ICE of a different kind). Hopefully, it will be resurrected sometime in the future. In the meantime, let me say a bit about our thinking behind the project.
A new way to teach math
The above section title is not really accurate; and that’s part of the point. In today’s world, the focus should no longer be on teaching but learning. And, in fact, that shift in perspective has been underway for several decades. What has slowed down the change in K-12 math education is that we are attempting to change the direction of a very large ocean vessel that has been steaming along for many hundreds of years. (You can tell it’s slow, since the term “steaming ahead” still applies, even though steamships died out long ago.)
To some extent, our philosophy was described in a book I wrote in 2011, titled Mathematics Education for a New Era.
Before we had technological tools to perform calculations and the myriad of mathematical procedures that we use to solve problems, learning mathematics required mastering all of those procedures. There was no other way to do it. By the time I went to university in 1965, the mental arithmetic skills I’d had to acquire to get there were no longer essential; the world had (electronic) calculators. And by the end of the Millennium, all the techniques I worked hard to master to get my math degree were no longer essential learning either.
The nature of doing mathematics had changed fundamentally. Executing procedure was now (all) done by machines; mathematics was about making effective use of those machines. (Farming changed significantly over the same period; and so too did many other professions.) I (and others) started to use the term “mathematical thinking” to refer to what mathematicians did – in their heads – when using the technology to solve problems.
This all happened over the course of my lifetime – what a time to have gone into math!
Mathematicians and other professionals who use mathematics switched to doing it the new way (using technology to do the procedural execution) fairly quickly.
But changing the way we teach it (and assessing that teaching’s effectiveness) is a much harder problem. The best (only?) way is to move from spending a lot of time on small skills (the nuts and bolts of mathematics) and use a project-based approach.
High Tech High in San Diego, CA took this approach about as far as you can go, and has obtained excellent results, but it remains one of a relatively small number of successful experiments that, for a several understandable reasons (most notably personnel with the required skillset), seem to be essentially impossible to scale up to national level.
What those experimental approaches have shown, however, is that the future of math learning lay with focusing not on “single-skill” problems, but on what are called “complex performance tasks.” Whereas “basic skills” (all now done faster and more accurately by machines) break down mathematics into its nuts-and-bolts, CPTs are at the (higher) level where the human brain naturally operates.
Consider: You can get only so far with “basic skills” when learning to play tennis, or ski, or play chess, or play a musical instrument (etc.). And such an approach would be boring to boot. But if the focus is not on the basic steps, but on the playing (of tennis), the skiing, the chess, playing the piano, etc., then the human brain comes into its own.
That was the key idea behind our approach. I coined the term “instruments for learning (mathematics)” for the CPTs we developed for our educational suite. [I gave a number of conference presentations on this approach; see for example this one from 2014.]
One of the factors that (obviously) makes the “learning it by doing it” approach work so well is that activities like those I listed are enjoyable things that people like to do. They are all play – the mechanism that Mother Nature, in her natural selection fashion, has developed for the young of all the “higher” creatures to learn the skills they need to survive. (Type “kittens” or “puppies” into YouTube for thousands of examples.)
So we accepted from the start that our CPTs should be presented as games. In our case we chose videogames (more specifically, puzzle-based games), but that was in part because, living in Silicon Valley, we knew some videogame developers. (I was a consultant at one large studio.) The other reason was that a videogame, if well designed, could be mastered without the need for help from others.
The requirement of creating games presented a considerable challenge.
Formulating CPTs as interactive digital tasks is relatively straightforward. Note that modifier “relatively”. You do have to make sure that when a student successfully completes the digital task, they have in fact “done the math” you want them to master.
You definitely want to prevent unreflective trial-and-error from leading to a solution. One obvious way to achieve that is to design the task so that the game solution (or solutions) you have in mind involves the same logical steps as using the traditional paper-and-pencil approach, yet there are overwhelmingly many possible action sequences, so trial-and-error won’t work. This is the way we decided to go. But it was not easy.
The other constraint is that the task should be a genuinely enjoyable one. In other words, what we wanted to build should be bona fide digital puzzle games. By that, I don’t mean embed the puzzle in a game. That’s easy, and a common way to create “math learning games”. Rather, the game should be a digital embodiment of the mathematics puzzle itself. That is, the game should be another representation of the math problem. That was a far harder nut to crack. In fact, most of the attempts we made failed to meet this criterion.
It took a long time and the involvement of several smart puzzle designers, but in the end we developed a half dozen or so that met our requirements and eventually settled on three that worked really well. You can read about them here. [There are short videos that explain the mathematics the puzzles embody. You can even try the puzzles at no cost for one month.] But this is just one example to convey the general idea.
The point is, using a suite of CPTs (as we do) carves up mathematics in a different way; just as is the case with the classroom education provided by a school like High Tech High. [The link in the paragraph above also leads you to a mapping that shows how our puzzles connect to the mathematics Common Core State Standards. Both approaches are designed to yield the same mathematical skillset.]
What makes it possible to safely “leave out” a variety of specific curriculum topics is that, when the overall goal is “solving math problems” (i.e., mathematical thinking), the individual topics don’t matter. As Liping Ma argued in her November 2013 article in the Notices of the American Mathematical Society, if taught in terms of mathematical thinking, whole-number arithmetic alone is a sufficient base for an effective mathematics education. It’s not the content that matters; it’s the thinking!
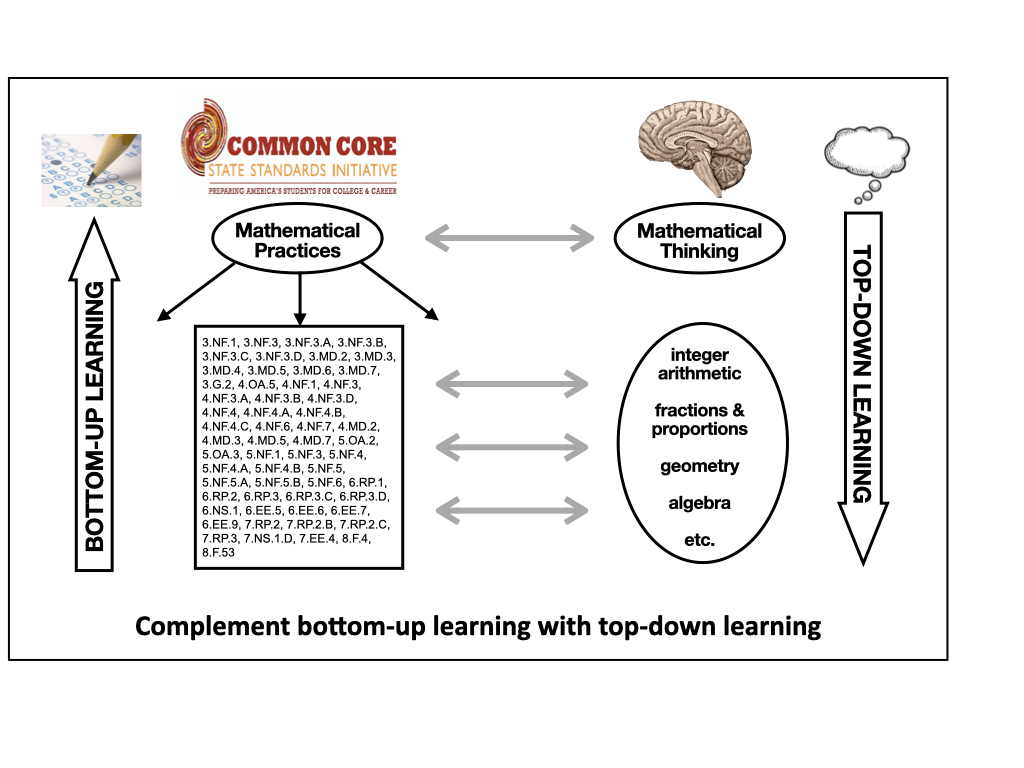
The Common Core developers knew that. Their Standards document leads off with what they call the “Mathematical Practices”. In our terminology, they are the key (definitional) components of mathematical thinking. Hitherto, CCSS-aligned education has largely (if not exclusively) focused on the individual curriculum topics (of which there are hundreds), leaving at best a faint hope that students will, in the process, pick up the Mathematical Practices (i.e., will learn to think mathematically).
To my mind, the way to begin making the shift towards a pedagogy built on acquiring the Practices directly (with technological tools doing the grunt work) is a hybrid approach illustrated by the diagram I led with. The classroom time saved by using technology to do procedural-execution in bottom-up lessons can be utilized to provide top-down learning in a variety of different ways (of which the stuff I and my colleagues have been working on is just one example).
Note that the “blood panel” approach lends itself to using our suite as a supplementary tool for learning. See the diagram.
But the approach could revolutionize assessment, where it really would be like a “blood panel” to assess your overall health.
At present, assessment of mathematical ability beyond basic skills requires hand-grading of student’s attempts to solve open-ended, multi-step problems, which is expensive and time consuming. But a digital tool like ours can obtain an assessment result in real-time. This, of course, is where validation by a large randomized trial is essential.
Working with WestEd, in 2021 we completed just one six month Dept of Education funded study on assessment, so we don’t have as much evidence for assessment use as we do for learning. Does our suite really cover goal 2, as that small WestEd study suggested? More generally, is it possible to find any small set of K-12 mathematical activities that suffice both for learning and assessment. Neither we nor anyone else will know that until we can run studies again, and for now that’s off the table, at least in the US. Sad. The American electorate is a mysterious entity.
