As I think about what all teachers of calculus should know, even if they are never going to explicitly use it in class, complex numbers immediately come to mind because they give insight into what is happening when you do calculus on the real line. Over the next several months I want to share some of the insights that come from doing calculus over the field of complex numbers. This will not be a course in complex analysis. Instead, I intend a sampling of ways in which complex analysis can illuminate what is happening. In particular, I would like to explore what happens when ordinary real calculus moves onto the complex plane, denoted by $\mathbb{C}$.

It is worth mentioning that complex numbers can be added, subtracted, multiplied, and divided and that $\mathbb{C}$ is $complete$ as defined last month, which means that every Cauchy sequence converges.

Borel's theorem also holds in the complex plane with open intervals replaced by open sets. A set $\mathcal{S}$ is $\textit{open}$ if every point of $\mathcal{S}$ is contained in an open disc that is entirely within $\mathcal{S}$. A set $\mathcal{S}$ is {\it closed\/} if it includes all of the points on the boundary. A points $\alpha$ is a $\textit{boundary point}$ of $\mathcal{S}$ if every open disc centered at $\alpha$ contains points other than $\alpha$ that are in $\mathcal{S}$ and points other than $\alpha$ that are not in $\mathcal{S}$. In $\mathbb{C}$, Borel's theorem states that if a closed set is contained in the union of an infinite collection of open sets, then there is a finite subcollection of those open sets whose union still contains the entire closed set.

$\textbf{First}$, I will be exploring why complex numbers are the right way to think about polar equations. The basic relationship is Euler's discovery that $$ e^{i\theta} = \cos \theta + i\sin \theta. $$

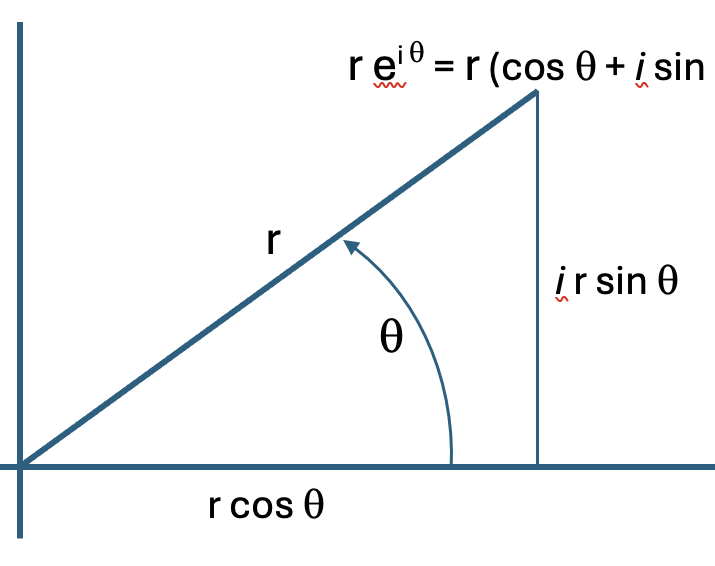
This means that each complex number can be represented in the form $re^{i\theta}$ where $r$ is the distance from the origin and $\theta$ is the angle measured counter-clockwise from the positive real axis. This explains what happens when we multiply two complex numbers, $$ re^{i\theta} \times s e^{i\phi} = rs e^{i(\theta+ \phi)}.$$ You multiply the magnitudes or distances from the origin and add the angles. How simple is that?

In a later column, I will explain how Euler came up with this remarkable insight, but for now I just want to mention that this gives me an easy way of remembering the sum of angles formulas for sine and cosine. Using the fact that $e^{i(\theta + \phi)} = e^{i\theta} \cdot e^{i\phi}$, we get that \begin{eqnarray*} \cos(\theta+ \phi) +i \sin(\theta + \phi)& = & e^{i(\theta + \phi)} \\ & = & e^{i\theta} \cdot e^{i\phi} \\ & = & (\cos\theta + i \sin\theta) (\cos \phi+ i\sin \phi) \\ & = & (\cos\theta \cos\phi - \sin \theta \sin\phi) + i(\sin\theta \cos \phi + \cos\theta \sin\phi) \end{eqnarray*} and therefore \begin{eqnarray*} \cos(\theta+ \phi) & = & \cos\theta \cos\phi - \sin \theta \sin\phi,\ {\rm and} \\ \sin(\theta + \phi) & = & \sin\theta \cos \phi + \cos\theta \sin\phi. \end{eqnarray*} Instead of trying to memorize these formulas, I simply rederive them from this simple observation every time I need them.

$\textbf{Second}$, interesting things happen when you differentiate a complex valued function. The definition of the derivative is the same, $$f'(x) = \lim_{y\to x} \frac{f(y)-f(x)}{y-x}.$$ But now things are complicated by the fact that $y$ could approach $x$ from $any$ direction. It does not even need to come in on a straight line. It may try to sneak in to $x$ by coming down along a parabolic or other arc. The amazing fact is that it is always enough to check that the limits exist whether you come in left or right (changing by a real amount) or top or bottom (coming from an imaginary amount). As long as these limits exist and agree, the function is differentiable at $x$.

For example, the Taylor series for $1/(1+x^2)$ expanded around 0 has radius of convergence 1 because this function does not exist at $\pm i$, and those point are one unit away from 0. If we want to expand $1/(1+x^2)$ around 1, the radius of convergence will be $\sqrt{2}$, the distance to $\pm i$. The Taylor series for the exponential function $e^x$ converges for all values of $x$ because it is differentiable for all complex values of $x$.

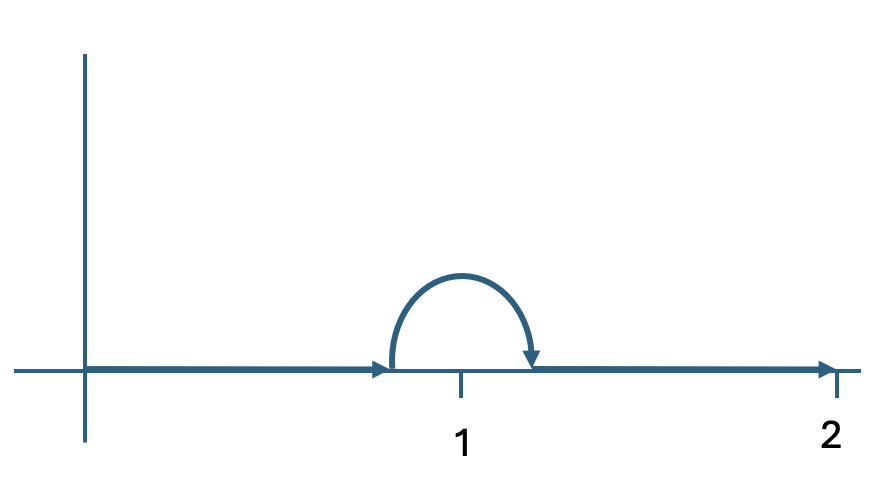
$\textbf{Third}$, integration gets very interesting. We no longer have to integrate along the real axis. We can integrate over any curve we wish. Let's say we want to integrate $1/(1-x)$ from 0 to 2. In standard, real-valued calculus this cannot be done because the function does not exist at 1. But in complex calculus, we can integrate along the real line until slightly short of 1, leave the real line to avoid that problem point, then come back on the far side of 1. Does it matter which way we go, either above or below the problem point? In this and most cases: $Yes!$ In this case, if I go above, the value of the integral is $\pi i$. If I go below, it is $- \pi i$. But amazingly, that is the only way in which the choice of path matters. $Every$ path that goes above 1 will produce an integral equal to $\pi i$ and every path that goes below will yield $-\pi i$.

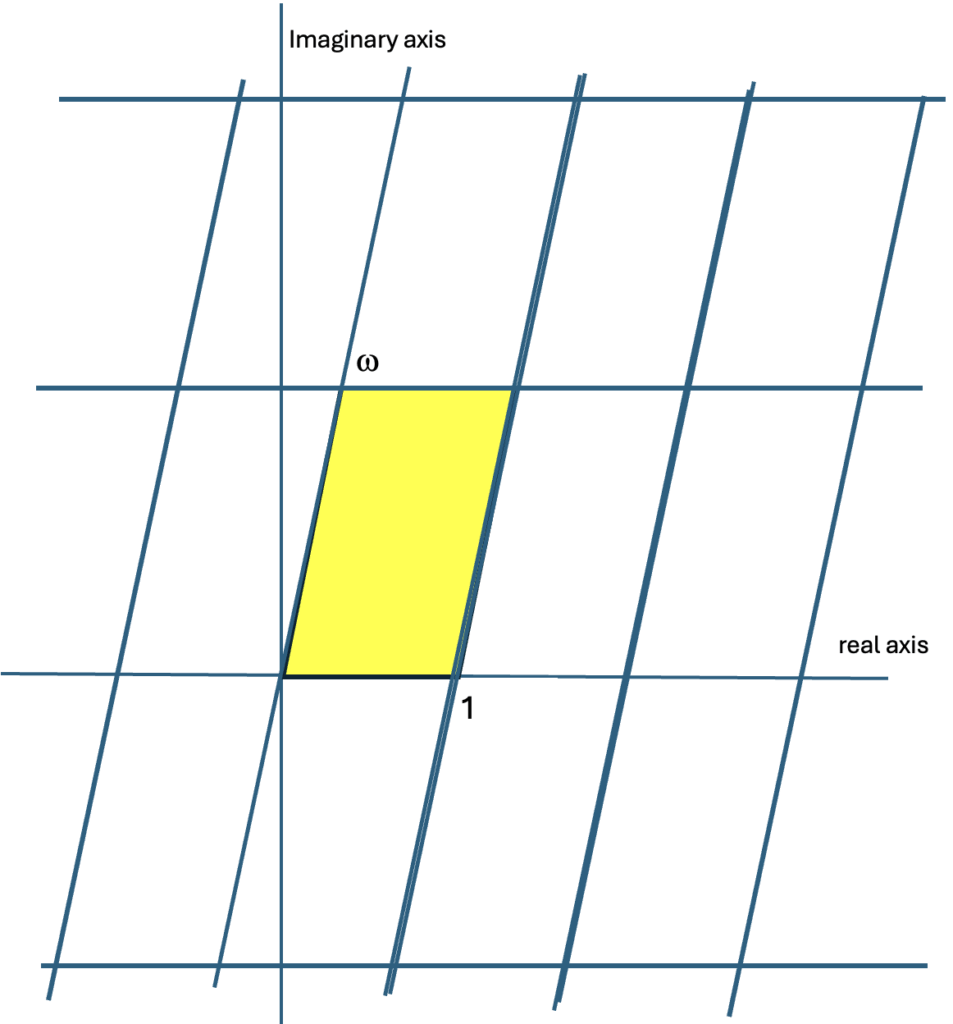
Integration is particularly interesting when a function has multiple points where it is not defined. This leads to new functions totally unanticipated when we limit ourselves to real numbers. I hope at some point to at least touch on the mysteries of elliptic functions (which have only a tenuous connection to ellipses). We all know that the sine function is periodic with period $2\pi$, $\sin x = \sin (x+2\pi)$. Euler's result implies that the exponential function has period $2\pi$ in the imaginary direction, $e^x = e^{x+2\pi i}$. It turns out that these are extreme cases of the elliptic functions which have two complex periods. We can always normalize so that one of the periods is 1 and other is a complex number with a positive imaginary part, call it $\omega$. An elliptic function $F$ satisfies $F(x) = F(x + m + n\omega)$ for every pair of integers $m$ and $n$. This means that we can tile the complex plane with parallelograms. The values in any one of these parallelograms will simply reappear in every other parallelogram. This may sound boring. In fact, it lies at the heart of some of the most exciting mathematics that is being researched today, mathematics that has included the proof of Fermat's Last Theorem, the fact there do not exist positive integers satisfying $a^n + b^n = c^n$ when $n$ is greater than or equal to 3.