MAA Section Lecturer Series
The MAA provides three Section Lecturer programs on a three-year rotation: the George Pólya Lecturer program and the MAA NAM and MAA AWM Section Lecturer programs. Each Section is eligible to invite a speaker from one of the programs each year.
George Pólya embodied the high quality of exposition that the Mathematical Association of America seeks to encourage. Beginning in 2022, the MAA is accelerating the rotation schedule for appointing a new Pólya Lecturer from five years to three years, and adding two new speaker programs, also on three-year rotations, to provide all Sections with a funded invited lecture every year!
The two new programs have been developed in partnership with the Association for Women in Mathematics (AWM) and the National Association of Mathematicians (NAM), to better engage the three organizations in an ongoing dialogue through participation at Section meetings: the MAA AWM Section Lecturer Program, and the MAA NAM Section Lecturer Program. The lectures are meant to be mathematical and the speakers will represent earlier-career mathematicians and serve to introduce audiences to new faces.
Each year, the Pólya, MAA AWM, and MAA NAM Lecturers will be notified as to which sections are eligible for a visit during that year. Sections should contact the lecturer directly to coordinate a visit.
View Lecturers by Program - MAA Pólya MAA AWM MAA NAM
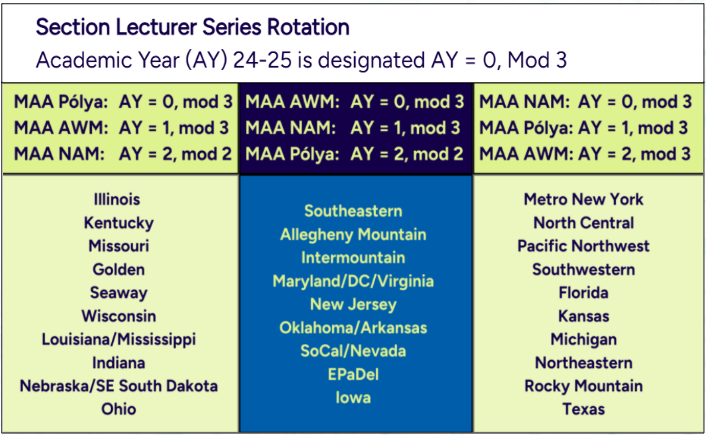
Section Lecturer Series Rotation
Academic Year (AY) 24-25 is designated AY = 0, Mod 3
It is customary for the Section to waive any registration, banquet, and social fees for the lecturer. The Lecturer will pay his/her own travel expenses and will be reimbursed for by the Association. Should, by accident, a section invite two speakers, it will be asked to reimburse the Association for the more expensive trip.
Reimbursement forms can be found here.
Each section is asked to be a thoughtful host. In the crush of meeting details and the distribution of duties amongst section officers and local arrangements faculty, it is sometimes easy for responsibilities to fall through the cracks. Please be sure to consider your visitors' arrangements for travel, lodging, meals, local transportation and registration. In the days of "Saturday night stay overs", it is especially cordial that the section considers Saturday evening dining arrangements. At least give visiting speakers options ("a ride would be great" or "I'll catch a cab") for airport pickups, get-togethers at meals, etc. Be sure to communicate fully about the schedule of events at your meeting.
If you are a lecturer and have any questions, a useful reference sheet can be found here. If the answer to your question is not on this document, please contact the MAA Communities Coordinator at communities@maa.org for assistance.
Speaker Information
Deanna Haunsperger
Carleton College
Email: dhaunspe@carleton.edu
Available as a speaker from Fall 2022 through Spring 2025
Bio: A former President of the Mathematical Association of America, Deanna Haunsperger has also served the MAA in numerous ways over the years, including as co-editor of Math Horizons, Second Vice President, co-chair of the Centennial Planning Committee, and Chair of the Council on Outreach. She is the 2021 recipient of the Yueh-Gin Gung and Dr. Charles Y. Hu Award for Distinguished Service.
Haunsperger is passionate about opening the doors of mathematics to everyone. To that end, she co-directed with Steve Kennedy the Carleton Summer Mathematics Program for Women 1995-2014, which the AMS named a Program that Makes a Difference.
Haunsperger is co-editor of several volumes, including The Edge of the Universe, A Century of Advancing Mathematics, 101 Careers in Mathematics, and Count Me In: Community and Belonging in Mathematics. She received the AWM M. Gweneth Humphreys Award for Mentorship of Undergraduate Women, the AWM President’s Award, and was an inaugural AWM Fellow.
Haunsperger is a Professor of Mathematics at Carleton College, where she has taught for over twenty-five years. She is married to fellow mathematician Steve Kennedy and has two adult children.
Additional information can be found here.
Topics include:
A Glimpse at the Horizon
What do a square-wheeled bicycle, a 17th-century French painting, and the Indiana legislature all have in common? They appear among the many bright stars on the mathematical horizon, or, um, in Math Horizons. Math Horizons, the undergraduate magazine started by the MAA in 1994 publishes articles to introduce students to the world of mathematics outside the classroom. Some of mathematics’ best expositors have written for MH over the years; here is an idiosyncratic tour of the first ten years of Horizons.
Halving Your Cake
Here is a problem as old as humanity: given a resource to be shared (water, land, cake), how can it be shared fairly between several people? The answer, in the case of two claimants, is simple and ancient and known to every five-year-old with a sibling: I cut; you choose. Things get much more interesting and challenging if one has more than one sibling. How do we make fair divisions?
Community and Belonging in Mathematics
How can building communities in mathematics help in our ongoing quest to make mathematics more inclusive? Social psychologists can teach us the importance of individuals feeling accepted, valued, and legitimate within their community—the importance of a sense of belonging. Successful communities can teach us the power, in the form of resilience and perseverance, that their members enjoy. Armed with this information, we can create communities to support members of underrepresented groups in mathematics.
Po-Shen Loh
Carnegie Mellon University
Email: hello@poshenloh.com
Available as a speaker from Fall 2023 through Spring 2026
Bio: Po-Shen Loh is a social entrepreneur and inventor, working across the spectrum of mathematics, education, and healthcare, all around the world. He is a math professor at Carnegie Mellon University and previous national coach of the USA International Mathematical Olympiad team. He has pioneered innovations ranging from a scalable way to learn challenging math live online at comparable engagement to live-streaming entertainment, to a new way to control pandemics by leveraging self-interest. As an academic, Po-Shen has earned distinctions ranging from an International Mathematical Olympiad silver medal to the United States Presidential Early Career Award for Scientists and Engineers. His scientific research considers a variety of questions that lie at the intersection of combinatorics (the study of discrete systems), probability theory, and computer science. As an educator, he was the coach of Carnegie Mellon University’s math team when it achieved its first-ever #1 rank among all North American universities, and the coach of the USA Math Olympiad team when it achieved its first-ever back-to-back #1-rank victories in 2015 and 2016, and then again in 2018 and 2019. His research and educational outreach takes him to cities across the world, reaching over 10,000 people each year through public lectures and events, and he has featured in or co-created videos totaling over 19 million YouTube views. Po-Shen received his undergraduate degree in mathematics from Caltech in 2004, graduating first in his class. He received a master’s degree in mathematics from the University of Cambridge in 2005, where he was supported by a Winston Churchill Foundation Scholarship. He continued his studies at Princeton, supported by a Hertz Foundation Fellowship and a National Science Foundation Graduate Research Fellowship, where he completed his Ph.D. in mathematics at the end of 2009, and has been on the faculty at Carnegie Mellon University ever since.
Additional information can be found here.
Topics include:
Sparking Social Impact By Using Math To Align Incentives
The scale of national and international societal problems can be daunting. One person, or even a small team, is minuscule relative to the number of people who require assistance. There is an area close to mathematics, however, which devises solutions in which problems solve themselves even through self-serving human behavior: Game Theory. The speaker is a pure math professor and researcher who transitioned to using Game Theory to develop new solutions for large-scale real-world problems. He will talk about his experience going from the ivory tower of academia into the practical mess of the real world, where he ultimately innovated fundamentally new approaches to pandemic control (https://novid.org) and advanced math education (https://live.poshenloh.com).
Steve Butler
Iowa State University
Email: butler@iastate.edu
Available as a speaker from Fall 2024 through Spring 2027
Bio: Steve Butler is an award-winning teacher. He has given talks at numerous venues ranging from the AMS-MAA address at Mathfest 2021 to the Iowa State Fair and almost everything in between.
Steve particularly enjoys working with young researchers. He regularly participates in the Iowa State REU and maintains a listing of REU sites for students (mathreuprograms.org); he is also a lead organizer of the Graduate Research Workshop in Combinatorics (GRWC).
Steve’s mathematics was heavily influenced by his mentors, Fan Chung and Ron Graham. His mathematical research includes spectral graph theory, shuffling, juggling, origami, tiling, Apollonian circle packings, parking functions, and more. In 2015, he became the 512th mathematician to have an Erdős number of 1.
Steve Butler has been at Iowa State University since 2011 where he is a Morrill Professor and the Barbara J Janson Professor of Mathematics. More information about him can be found online (stevebutler.org).
Additional information can be found here.
Topics include:
Juggling Counts
Mathematics is a language which can help us describe and explore patterns. One source of patterns that mathematicians have been exploring comes from juggling (the tossing of objects, usually balls or clubs). In this talk we will look at multiple ways to describe juggling patterns that allow us to find new juggling patterns, and to count how many possible patterns exist. We can compare answers to various problems to give a combinatorial proof of Worpitzky’s identity. We will also look at a few juggling-based problems that mathematics has not yet succeeded in answering.
Every Game I’m Shufflin’, Shufflin’
Shuffling is a well-known aspect of gameplay to help make the decks “sufficiently random” to make the game interesting. Shuffling is also a source of mathematical exploration where shuffles are thought of as permutations of the cards. In this talk, we will take some tools of mathematics, modular arithmetic, and binary numbers, and show how we can apply these to shuffling, and in particular, some simple-to-learn mathematically-based card tricks, which will be performed live. Along the way, we will also learn why we should never work with jokers.
Pamela E. Harris
University of Wisconsin Milwaukee
Email: peharris@uwm.edu
Available as a speaker from Fall 2024 through Spring 2027
Bio: Dr. Pamela E. Harris is a Mexican-American mathematician and serves as Associate Professor of Mathematics at the University of Wisconsin-Milwaukee. She received her BS from Marquette University and MS and Ph.D. in mathematics from the University of Wisconsin-Milwaukee. Dr. Pamela E. Harris’s research is in algebraic combinatorics and she is the author of over 70 peer-reviewed research articles in internationally recognized journals. She is a Fellow of the American Mathematical Society and of the Association for Women in Mathematics. Dr. Harris is also an award-winning mathematical educator, receiving the 2022 MAA’s Haimo Award for Excellence in Mathematical Education, the 2020 MAA Northeast Section Award for Distinguished Teaching, the 2019 MAA Alder Award for Distinguished Teaching by a Beginning Mathematics Faculty Member, and the 2019 Council on Undergraduate Research Mathematics and Computer Sciences Division Early Career Faculty Mentor Award. She is the President and co-founder of Lathisms: Latinxs and Hispanics in the Mathematical Sciences, cohosts the podcast Mathematically Uncensored, and is a coauthor of the books Asked And Answered: Dialogues On Advocating For Students of Color in Mathematics, Practices, and Policies: Advocating for Students of Color in Mathematics and Read and Rectify: Advocacy Stories from Student of Color in Mathematics.
Additional information can be found here.
Topics include:
Finding needles in haystacks: Boolean intervals in the weak order of $\mathfrak{S}_n$
Finding and enumerating Boolean intervals in W(Sn)W(\mathfrak{S}_n)W(Sn), the weak order of the symmetric group Sn\mathfrak{S}_nSn, can feel like trying to find needles in a haystack. However, through a surprising connection to the outcome map of parking functions, we provide a complete characterization and enumeration for Boolean intervals in W(Sn)W(\mathfrak{S}_n)W(Sn). We show that for any π∈Sn\pi \in \mathfrak{S}_nπ∈Sn, the number of Boolean intervals in W(SnW(\mathfrak{S}_nW(Sn with minimal element π\piπ is a product of Fibonacci numbers. This is joint work with Jennifer Elder, Jan Kretschmann, and J. Carlos Martínez Mori.
Multiplex juggling sequences and Kostant’s partition function
Multiplex juggling sequences are generalizations of juggling sequences (describing throws of balls at discrete heights) that specify an initial and terminal configuration of balls and allow for multiple balls at any particular discrete height. Kostant’s partition function is a vector function that counts the number of ways one can express a vector as a nonnegative integer linear combination of a fixed set of vectors. What do these two families of combinatorial objects have in common? Attend this talk to find out!
How to choose your own mathematical adventures
What is mathematical research? How does a mathematician find problems to work on? How does one build mathematical collaborations? In this talk, I will share my journey to research mathematics, what it entails, how I have developed new research ideas, and how I have found my place within the mathematical community. Mathematical topics of discussion will include lattice point visibility, parking functions, and a connection between vector partition functions and juggling. No prior mathematical background on these topics is expected nor assumed as we will introduce all of the needed concepts from first principles. All that is needed is the willingness to wonder and ask the question: “What happens if…?”
Francis Su
Harvey Mudd College
Email: su@math.hmc.edu
Available as a speaker from Fall 2025 – Spring 2028
Additional information can be found here.
Catherine Hsu
Swarthmore College
Email: chsu2@swarthmore.edu
Available as a speaker from Fall 2022 through Spring 2025
Bio: Catherine Hsu is an Assistant Professor in the Department of Mathematics and Statistics at Swarthmore College. Her mathematical interests began as a penchant for logic puzzles and problem solving and grew into a love of abstract algebra and Galois theory while she was an undergraduate student at Rice University. Her research is now primarily in algebraic number theory, including projects related to modular forms and Apollonian circle packings. She also enjoys thinking about mathematical exposition, pedagogy, and unnecessarily complicated strategies for the card game Hanabi.
Prior to joining Swarthmore in the fall of 2020, Hsu was a Heilbronn Research Fellow at the University of Bristol as well as an AAUW American Dissertation Fellow and a Doctoral Research Fellow at the University of Oregon. As a junior researcher, she has greatly enjoyed traveling and speaking at conferences around the world and is looking forward to meeting new mathematicians as part of the MAA-AWM Lecturer program.
Additional information can be found here.
Topics include:
Prime Components in Apollonian packings
An Apollonian circle packing is a fractal arrangement formed by repeatedly inscribing circles into the interstices in a Descartes configuration of four mutually tangent circles. The curvatures of the circles in such a packing are often integers, and so it is natural to ask questions about their arithmetic properties. For example, it is known by work of Bourgain-Fuchs that a positive fraction of integers appear as curvatures in any integral Apollonian circle packing. In this talk, we investigate the arithmetic properties of the collection of integers appearing in “thickened prime components” of Apollonian circle packings.
Projective and Non-Abelian SET
Mathematicians love SET. On the surface, this classic game is a con test of pattern recognition, but it also presents an interesting way to visualize the geometry of a torus over a finite field. In this talk, we will discuss some of the mathematics connected to SET and then explore several new versions of the game, including one arising from projective geometry and one arising from non-abelian groups. In particular, we will see how these non-abelian variations on SET can give intuitive visualizations of abstract group structures.
Small Eisenstein Congruences and Explicit Non-Gorenstein R = T
In his seminal work on modular curves and the Eisenstein ideal, Mazur studied the existence of congruences between certain Eisenstein series and new forms, proving that Eisenstein ideals associated to weight 2 cusp forms of prime level are locally principal. In this talk, we’ll explore generalizations of Mazur’s work to squarefree level, focusing on some work in progress, joint with Preston Wake and Carl Wang-Erickson, that establishes a computable algebraic criterion for having R = T in a certain non-Gorenstein setting.
Ranthony A. Clark
Duke University
Email: ranthony.clark@duke.edu
Available as a speaker Fall 2024 through Spring 2027
Bio: Ranthony A. Clark is a National Science Foundation Ascending Postdoctoral Fellow, Phillip Griffiths Assistant Research Professor, and Computational and Mathematical Science Fellow for the Center for Computational Thinking at Duke University. She earned a PhD in Mathematics in 2018 from the University of Iowa and her research interests include applied algebraic topology, data science, commutative ring theory, math education, and the history of Black mathematicians.
Dr. Clark is deeply invested in quantitative justice, that is, using mathematical tools to address societal issues rooted in inequity. Her current work in quantitative justice involves applications of mathematics and data science to electoral redistricting. She was a Berlekamp Postdoctoral Fellow for the Fall 2023 Semester program on Algorithms, Fairness, and Equity at the Simons Laufer Mathematical Sciences Institute (SLMath) and currently works with the Quantitative Gerrymandering Group in the Department of Mathematics at Duke University. Recently, she became an inaugural member of the Race and Redistricting Expert Project (RREP) 2024 class through the Southern Poverty Law Center.
Additional information can be found here.
Topics include:
Quantitative Justice: Using Math to Change the World
Quantitative Justice comprises the mathematical, computational, and statistical analysis of real world problems related to social inequity. In this context, mathematical tools are used to quantify notions of ‘fairness’ in a given domain, generating both new mathematics and impacting society at large.
In this talk we will introduce this emergent new field of interdisciplinary research. In particular, we will give current examples of how math like statistics, metric geometry, and topological data analysis is being used to shift societal systems, and discuss how this research complements historical and current efforts to broaden participation in the mathematical community through scholarship, teaching, and service.
Death to Determinants
Determinants? Who needs them? “Computing the characteristic polynomial C(x) of a square matrix A as the determinant of the matrix xI-A is like programming in LISP, Lots of Irritating Single Parenthesis.”
The above quote is pulled from the introduction of a paper written by Dr. William McWorter, Jr. the first Black person to earn a PhD in mathematics from Ohio State, which described a determinant-free algorithm for the characteristic polynomial. Dr. McWorter, among many things, aimed to have as one of his mathematical contributions—the ‘dearth’ of determinants in linear algebra.
In this talk, we will discuss McWorter’s algorithm, and the larger project from which it came–Hidden Figures Revealed. Along the way I will discuss how I have used storytelling as a tool in research and teaching to build community in mathematics.
Political Geometry: Metric Based Approaches to Shape Comparison in Redistricting
In this talk we introduce the concept of a metric space, and motivate the use of metrics as a tool for shape comparison. By representing an object as a finite metric space, we can utilize families of metrics like Hausdorff and Gromov-Hausdorff distances to develop similarity measures between shapes.
One particular focus is on applications to electoral redistricting, where the notion of shape is ubiquitous when investigating the political geography of a state. In particular, we will discuss how metrics were used in a recent effort to quantify the idea of ‘communities of interest’ in the 2021 redistricting cycle.
Emilie Purvine
Pacific Northwest National Laboratory
Email: Emilie.Purvine@pnnl.gov
Available as a speaker Fall 2023 through Spring 2025
Bio: Dr. Emilie Purvine is a mathematician and data scientist at Pacific Northwest National Laboratory. She joined PNNL in 2011 after receiving her PhD in mathematics from Rutgers University with a focus on enumerative combinatorics and nonlinear recurrence relations. While at PNNL Emilie has had the opportunity to contribute to a variety of projects tackling hard problems in applications including computational biology and chemistry, power grid modeling, cyber network analysis, and knowledge models. Her current mathematical research focus is on topological data analysis applied to discrete structures like graphs and hypergraphs. Much of her work involves finding mathematical nuggets in applied domains and working on theoretical advances to enable operational progress.
Emilie also greatly values the ability to make mentoring a focus of her work. She loves to give presentations to students at all levels to provide an example of what a mathematician can do outside of academia. Interns and postgraduates (2-3 year temporary employees including post bachelors, post masters, and postdoc) are always included into her projects to promote on the job learning.
Outside of her core work activities Emilie has also been the chair of the MAA’s Membership Committee and an associate editor of the AMS Notices. In her free time Emilie spends time with her friends and family, enjoys a good book, loves the outdoors and traveling to new destinations.
Additional information can be found here.
Topics Include:
Mathematics for Cyber Security
The security of computer networks is crucial to maintain data privacy, intellectual property rights, and even to keep infrastructure functioning reliably. One might think that cyber security is the responsibility of computer scientists and network administrators. This is certainly true, but as adversaries change their tactics and become increasingly sophisticated, mathematicians are lending a hand. In this talk I will begin by introducing the landscape of computer networks, the cyber kill chain, and cyber security operations. I will present some of the main challenges facing cyber security today and show how mathematicians, like myself, are applying their skills in data modeling, anomaly detection, and machine learning to help provide situational awareness and keep computer networks resilient.
Graphs and Hypergraphs and Topology, Oh My!
Mathematical structures and concepts can be great models of real-world data. For example, differential equations have a long history of success in applied mathematics to model dynamics found in rivers and oceans, the atmosphere, and molecular systems (just to name a few!). Network science is an area of applied math that uses graph structures to model relational systems like social, collaboration, and transportation networks. Graphs, however, are limited to modeling pairwise relationships among entities. Hypergraphs and topological spaces provide alternate models of relational systems that allow for arbitrary sized and structured relationships. In this talk I will introduce the mathematical concepts of graphs, hypergraphs, and topology and show how they are used to model real-world data from a variety of applications including biological systems, chemistry measurements, and cyber networks. We’ll also talk about what measurements and properties of these structures can tell us about the systems they model.
Karen Lange
Wellesley College
Email: klange2@wellesley.edu
Available as a speaker Fall 2023 through Spring 2025
Bio: Karen Lange is the Theresa Mall Mullarkey Associate Professor of Mathematics at Wellesley College. In her research, she studies the “balance scales” used to calibrate computational information and applies these tools to measure the difficulty of algebraic problems. She’s also passionate about community-building and inclusion in mathematics, and she teaches a seminar on writing about mathematics for the public. She earned her undergraduate degree at Swarthmore College and her doctoral degree at the University of Chicago, and she completed an NSF Postdoctoral Fellowship at the University of Notre Dame.
Additional information can be found here.
Topics Include:
Different Problems, Common Threads: Computing the difficulty of mathematical problems
Mathematics is filled with theorems that state the existence of a desired object. For example, a result known as Weak Kőnig’s Lemma (which I’ll introduce) states that “every binary tree with infinitely many nodes has an infinite path”. But just because we know an object exists, doesn’t mean we can find it. Given Weak Kőnig’s Lemma, it’s natural to ask whether we can compute a path through a given binary tree with infinitely many nodes. It turns out the answer to this “Path Problem” is “no”, so we say that the problem is not “computable”. But then just what exactly is the computational power of this Path Problem?
Using this Path Problem as a test case, we will explore the key ideas behind taking a “computable” perspective on mathematics (over an “existence” one) and describe an approach for measuring the computational power of mathematical problems. We’ll see that the computational power of problems varies widely and studying problems’ power helps to illuminate what really makes problems “tick”.
Classification via lists in computable structure theory
“Classifying” a natural class of structures is a common goal in mathematics. Providing a classification can mean different things, e.g., determining a set of invariants that settle the isomorphism problem or instead creating a list of all structures of a given kind without repetition of isomorphism type. Here we’ll discuss classifications of computable structures of the latter kind and provide a self-contained introduction to computable structure theory along the way. We’ll consider natural classes of computable structures such as vector spaces, equivalence relations, algebraic fields, and trees to better understand the nuances of classification via effective lists and its relationship to other forms of effective classification.
Lauren Keough
Grand Valley State University
Email: keoulaur@gvsu.edu
Available as a speaker Fall 2024 through Spring 2027
Bio: Lauren Keough is an associate professor in the Department of Mathematics at Grand Valley State University. Her favorite activities as a child in Rhode Island were those that allowed room for creativity, so, at first, she wasn’t a huge math fan. In fact, when she used her creativity to find patterns to do timed multiplication tests, she thought she was cheating. Her love for math started to develop as an undergraduate at Hofstra University where she learned she could be creative in her math courses. Lauren completed her PhD in 2015 at the University of Nebraska – Lincoln under the supervision of Dr. Jamie Radcliffe. Her PhD research is in extremal graph theory, and she especially loves areas where she can involve undergraduates. After graduate school, Lauren spent a year at Davidson College as a visiting assistant professor before moving to Grand Valley State University (GVSU) in 2016. At GVSU, Lauren strives to meet the needs of all undergraduates. She spreads her love of math by mentoring undergraduate research, hosting math circles, and teaching as many different courses as possible. Beyond math, Lauren likes to do crossword puzzles and is learning to embrace winter sports.
Additional information can be found here.
Topics include:
Breaking Graph Symmetries
A graph is a set of vertices (dots) connected by edges (line segments). When drawn, graphs can have many symmetries. We can model symmetries using automorphisms – maps that change the labels of the vertices, but not the structure. One way to break symmetry is to “paint” the vertices so that the only color-preserving automorphism is trivial. We call such a painting a distinguishing coloring. From another perspective, we can consider how many vertices we need to “pin down” so that if those vertices don’t move, no vertices can move in an automorphism. We call a such a subset of the vertices a determining set. We will discuss distinguishing colorings and distinguishing sets for several types of graphs, and a conjecture that was recently proved by some GVSU undergraduates.
My Two Word Teaching Philosophy
Teaching can be incredibly hard, and it’s easy to lose sight of the big picture. In this talk I will discuss what happened when I embraced a two word teaching philosophy: empathy first. This attitude has changed what I do in my classroom – assessment techniques, activities, and what I value. In a time when I both feel a need for radical change and am just so tired, I’ll try to offer some concrete things I’ve tried, both big and small from efficient and effective ways to implement different assessment techniques to conversations with struggling students. This talk is a tribute to everyone I’ve ever had the privilege of talking about teaching with, including my students: I’ve learned something from all of you!
Math Circle Magic for All
One of my favorite ways to interact with people is through doing problems that people don’t always think of as “math”. I’ve led math circles at GVSU for several years and will present some of my favorite problems. Some of these are magic tricks, and some are just magical in the cool math one discovers while exploring them. This will be an interactive talk where audience members get to discuss math-ish problems with each other and will (hopefully) get to leave with a new discovery of their own.
Noella Sawyer
Southwestern University
Email: sawyern@southwestern.edu
Available as a speaker from Fall 2025 – Spring 2028
Additional information can be found here.
Elisa Bellah
Carnegie Melon University
Email: ebellah@andrew.cmu.ed
Available as a speaker from Fall 2025 – Spring 2028
Additional information can be found here.
Lorin Crawford
Microsoft Research New England
Email: lcrawford@microsoft.com
Available as a speaker Fall 2022 through Spring 2025
Bio: Lorin Crawford is a Senior Researcher at Microsoft Research New England. He also holds a position as the RGSS Assistant Professor of Biostatistics at Brown University. His scientific research interests involve the development of novel and efficient computational methodologies to address complex problems in statistical genetics, cancer pharmacology, and radiomics (e.g., cancer imaging). Dr. Crawford has an extensive background in modeling massive data sets of high-throughput molecular information as it pertains to functional genomics and cellular-based biological processes. His most recent work has earned him a place on Forbes 30 Under 30 list, The Root 100 Most Influential African Americans list, and recognition as an Alfred P. Sloan Research Fellow and a David & Lucile Packard Foundation Fellowship for Science and Engineering. Before joining Brown, Dr. Crawford received his PhD from the Department of Statistical Science at Duke University and received his Bachelor of Science degree in Mathematics from Clark Atlanta University.
Additional information can be found here.
Topics include:
Interpretability in Black Box Statistical Methods
A consistent theme of my work is to take modern statistical and machine learning approaches and develop theory that enable their interpretations to be related back to classical principles in biology. The central aim of this talk is to address variable selection questions in “black box” nonlinear and nonparametric regression. Motivated by statistical genetics, where nonlinear interactions are of particular interest, we will introduce novel, interpretable, and computationally efficient ways to summarize the relative importance of predictor variables. These approaches both (1) capture nonlinear structure of data and (2) provide significance measures for powerful variable selection.
Variable Selection with 3D Shapes
The recent curation of large-scale databases with 3D surface scans of shapes has motivated the development of tools that better detect global-patterns in morphological variation. Studies which focus on identifying differences between shapes have been limited to simple pairwise comparisons and rely on pre-specified landmarks (that are often known). In this talk, we present statistical pipelines for analyzing collections of shapes without requiring any correspondences. Our method takes in two classes of shapes and highlights the physical features that best describe the variation between them.
Haydee Lindo
Harvey Mudd College
Email: hlindo@hmc.edu
Available as a speaker Fall 2022 through Spring 2025
Bio: Dr. Haydee Lindo is an assistant professor of mathematics at Harvey Mudd College. Dr. Lindo is from Jamaica and earned her BAs in mathematics and political science. She received her Ph.D. in mathematics from the University of Utah and was previously a Gaius Charles Bolin Fellow and, later, an assistant professor of mathematics & statistics at Williams College. Dr. Lindo is a commutative algebraist with research interests in homological algebra and representation theory. She focuses on the development and application of the theory of trace modules over commutative rings.
Additional information can be found here.
Topics Include:
Introduction to trace ideals and centers of endomorphism rings
In many branches of mathematics, the full set of “functions” between two objects exhibits remarkable structure; it often forms a group and in some special cases it forms a ring. In this talk, we will discuss this phenomenon in Commutative Algebra. In particular, we will talk about the endomorphism ring formed by the homomorphisms from a module to itself by first looking at commuting square matrices with real entries. The well-known trace map on matrices can be generalized to a map on any module over a commutative ring. The image of such a map is a trace ideal. I’ll introduce the trace ideal and explain its role in the question “What properties of a module does its endomorphism ring detect?”
Stable Trace Ideals and Arf Rings
In this talk we will explore the intersection of notions of an ideal being “trace” and an ideal being “stable” that is, ideals that map to themselves under all homomorphisms to the base ring and ideals that isomorphic to their endomorphism rings. Following Lipman’s seminal work exploiting the nice properties of stable ideals to study Arf rings, we apply our results, incorporating the modern theory of trace ideals, to show that Arf rings enjoy even more geometric and homological properties than previously known. This is joint work with Dr. Hailong Dao.
Candice R. Price
Smith College
Email: cprice@smith.edu
Available as a speaker Fall 2023 through Spring 2025
Bio: My name is Candice Price, and I am currently an associate professor in the department of Mathematics at Smith College in Northampton MA. I was born and raised in California and earned a bachelor’s degree (2003) from California State University, Chico, and a master’s degree (2007) from San Francisco State University, both in mathematics. I earned my doctoral degree (2012) in mathematics from the University of Iowa under the advisement of Isabel Darcy. My area of research is applied mathematics, with an emphasis on mathematical models for biological questions. I also have research interests in math education and problems in the intersection of mathematics and social justice. In my teaching, research, and service, I focus on a collaborative approach and view my work through the lens of inclusion and diversity.
Additional information can be found here.
Topics Include:
Can we make grace the norm in our classrooms?
For much of my life, I was always confused about the way that people perceived the relationship between students and instructors in the classroom, especially in mathematics. There is such an adversarial relationship that even sharing my career choice with strangers leads to groans and stories of trauma. I believe this is what happens in a classroom without grace. So when we add grace the opposite should happen, right? During our time together, I hope to discuss with you the ways that I incorporate grace in my classroom and why many people think it is radical. I invite everyone to come and reflect on ways they can make grace the norm in their classrooms and spaces.
Using Mathematics to Unlock Biological Mysteries
Mathematical modeling is an effective resource for biologists– it provides ways to simplify, study and understand the complex systems common in biology and biochemistry. Many mathematical tools can be applied to biological problems, some traditional and some more novel, all innovative. This presentation will review some of the mathematical tools that I use to study biological questions including knot theory applied to DNA-protein interactions and using social networks to study evolutionary success.
Viewing the World through a Mathematical Lens
The way that numbers interact within the world has fascinated me from an early age. My research path has lead me to work on problems that are essentially about viewing the world through a mathematical lens. While discussing my journey to a career in Mathematics, I will share with you some of my favorite mathematical applications, including but not limited to DNA knotting, fighting parasites and Gerrymandering organs.
Opel Jones
Johns Hopkins University Applied Physics Laboratory
Email: opel.jones@jhuapl.edu
Available as a speaker Fall 2023 through Spring 2025
Bio: Opel is a loving husband, dedicated father, and servant to the community. He mentors, tutors, volunteers in his free time through his fraternity, and coaches youth football and youth baseball. Throughout the years, Opel has worked as an engineer, mathematics and statistics lecturer, development officer, and computer scientist, at several institutions and the federal government. He also served as Director of the Leadership Institute for several years at Hampton University, teaching leadership studies and developing leaders in addition to teaching mathematics and honors seminars. Currently, he is a mathematician and analyst at The John’s Hopkins University Applied Physics Laboratory. Additionally, he is currently serving on the County Council in Howard County, Maryland. He was first elected to office in 2018, and just re-elected in 2022.
Opel earned the B.S. in mathematics from Hampton University, the M.S. in mathematics from Howard University, and the Ph.D. in mathematics also from Howard University. He is a Life Member of Alpha Phi Alpha Fraternity, Inc., initiated at Hampton University, and past president of the local Howard County chapter. His professional associations include the American Mathematical Society, the Mathematical Association of America, and the National Association of Mathematicians. Opel loves music, football and baseball, reading, Sudoku puzzles, and is a lifelong practitioner of martial arts. He and his wife, Shaundra, are extremely proud parents of three: Opel II, Ivan, and Whitley!
Topics Include:
Mathematical Modeling in a STEM Realm
In my work at The Johns Hopkins University Applied Physics Laboratory, it is exciting and refreshing to use my mathematical and statistical background for real-world problems and situations. Whether using mathematical modeling to predict flight path, utilizing maximum likelihood estimation to estimate reliability, or implementing principles of systems engineering and computer science for systems analysis and test and evaluation, mathematics is at the core of planning in times of potential defense. In this talk, we will discuss several methods in which we evaluate system error, use data derived modeling to predict flight path, and solve real-world problems which our government may use.
To teach or not to teach?
Throughout my professional career, I have enjoyed my vocation as a systems engineer, lecturer, higher education administrator, computer scientist, clinical assistant professor, and now a mathematician and analyst. My background is in pure mathematics, specializing in enumerative combinatorics, something I may not use in my day-to-day work, yet the analytical skills and dynamic thinking that arises from the field is crucial for producing imperative results. In this talk for undergraduate and graduate students, we will discuss various paths to a fruitful career if one holds (or is pursuing) mathematical and/or statistical degrees at the terminal level.
Pattern Avoidance in Restricted Permutations
In 1974 Dumont found two types of permutations are counted by the same sequence. The first type is a permutation in which each even entry is followed by a smaller entry, and each odd entry is followed by a larger entry, or ends the permutation. The second type is a permutation wherein if an entry is a deficiency, it must be even, and if an entry is an exceedance or a fixed point, it must be odd. These are now known as Dumont permutations of the first and second kinds. There are two other types of permutations which are also counted by the same sequence, known as Dumont permutations of the third and fourth kinds. In this talk we will discuss several enumerations of restricted Dumont permutations, that is Dumont permutations avoiding certain patterns. We will also briefly discuss their proofs which involve methods using induction, block decomposition, Dyck paths, and generating functions. We will conclude with a conjecture that the patterns 2143 and 3421 are indeed Wilf-equivalent on Dumont permutations of the first kind.
Brett Jefferson
Pacific Northwest National Laboratory Email: brett.jefferson@pnnl.gov
Available Fall 2024 through Spring 2027
Bio: Dr. Brett Jefferson is a senior data scientist and team lead of the Human Factors and Interactions team at Pacific Northwest National Laboratory. He joined PNNL in 2018 after graduating from Indiana University’s Mathematical Psychology Laboratory. In his work, Brett focuses on studying patterns in complex data sets. Predominantly using topology, Brett maps patterns in data to observable and actionable behaviors from humans. By understanding these relationships Brett uncovers not only insight into human cognition, but also interesting mathematical constructions.
In addition to his technical work at PNNL, Brett also serves on the board of directors for the National Association of Mathematicians, Inc. NAM has a 50+ year history of support underrepresented groups in their mathematics education and career with a focus on African Americans. Brett began his second term in 2024.
Additional information can be found here.
Topics include:
Some Questions in Antihomology and Applications
The Vietoris Rips complex is well studied. However, what happens when the inequality is reversed? This talk will cover some findings by myself and others around persistent homology of this construction and where it may be useful in the real world.
Changing Directions: Building a Unique Career within and outside of Mathematics
This talk will discuss non-academic career paths with a background or degree in mathematics. I’ll have heavy emphasis on what a career at a national laboratory is like and also touch on themes of navigating graduate school, being black in the mathematical sciences, and the value of work-life balance
Nathan Alexander
Morehouse College
Email: nathan.alexander@howard.edu
Available as a speaker from Fall 2025 – Spring 2028
Additional information can be found here.
Reginald McGee
Haverford College
Email: rmcgee@haverford.edu
Available as a speaker from Fall 2025 – Spring 2028
Additional information can be found here.
Questions about Section Lecturers? Email MAA Communities at Communities@maa.org