Evolution of a Computer Application
In this article I discuss the process of producing a computer software system for mathematical research or instruction. I show how a mathematician can create a special-purpose computer language to facilitate development of a system.
John J. Wavrik is Professor of Mathematics at the University of California, San Diego.
Mathematical work benefits from the use of software that can be modified and extended as it is used. I show the process of creating a software system of this type by discussing several critical stages in the development of Groups32, a system for working with groups of low order.
Editor's note: This article is presented in two forms, HTML and PDF. The former is our "publication of record" in our standard format. The author intends this article to be read while using the associated computer programs. You may prefer to use the PDF file, which was designed to facilitate reading while interacting with the software. The article is long. If you prefer to read offline, you can download both the PDF file and the associated software. For more details on using the PDF file, read the author's Tips for Reading this Article -- or, if you know already that you want to read in PDF format (whether online or offline), go right to that version, which also contains the reading Tips and software links.
Resource note: A version of the Groups32 system being discussed in this article is accessible on the Internet at Groups32 Web page. This Web page contains instructions for accessing Groups32 via telnet and some written material including a sample session. This version has been used with classes and in REU projects.
Published September, 2003
© 2003, John J. Wavrik
Evolution of a Computer Application - Abstract
In this article I discuss the process of producing a computer software system for mathematical research or instruction. I show how a mathematician can create a special-purpose computer language to facilitate development of a system.
John J. Wavrik is Professor of Mathematics at the University of California, San Diego.
Mathematical work benefits from the use of software that can be modified and extended as it is used. I show the process of creating a software system of this type by discussing several critical stages in the development of Groups32, a system for working with groups of low order.
Editor's note: This article is presented in two forms, HTML and PDF. The former is our "publication of record" in our standard format. The author intends this article to be read while using the associated computer programs. You may prefer to use the PDF file, which was designed to facilitate reading while interacting with the software. The article is long. If you prefer to read offline, you can download both the PDF file and the associated software. For more details on using the PDF file, read the author's Tips for Reading this Article -- or, if you know already that you want to read in PDF format (whether online or offline), go right to that version, which also contains the reading Tips and software links.
Resource note: A version of the Groups32 system being discussed in this article is accessible on the Internet at Groups32 Web page. This Web page contains instructions for accessing Groups32 via telnet and some written material including a sample session. This version has been used with classes and in REU projects.
Published September, 2003
© 2003, John J. Wavrik
Evolution of a Computer Application - Introduction
I address this article to mathematicians and mathematics educators. It is not about the use of a piece of software but rather about a methodology for producing software and about the electronic representation and manipulation of mathematics. In the article I show how a mathematician can produce a special purpose language for a subject area to facilitate writing programs in that area.
Computer programs are often "end products" like books -- they remain relatively fixed after creation. The design and implementation of large software projects are most often in the hands of teams of experts in computer programming. The end user is not interested in the programming language or the developmental techniques, and, in fact, these things become invisible in the end product. The choice of language, however, can be a significant factor for ease in development, maintenance, and modification.
In this article I discuss production of dynamic software systems that are targeted at specialized research and instructional areas and are extended and modified as part of their use. The user, designer, and implementer are often the same person. We need, for this work, a language and methodology that allow software to be developed and modified easily. We need to make it feasible for a mathematician, whose expertise lies in other areas, to become involved in the task of creating languages and software systems.
A source of difficulty in programming with conventional general purpose languages is the gap between the means of expression provided by the language and the concepts of the subject area. We can reduce this gap by using a language specifically designed for a particular subject area. To do this in the realm of conventional compiled languages would require writing a custom compiler -- a formidable task. I will discuss and illustrate an approach that is the moral equivalent of writing a compiler but that is viable for a working mathematician.
It has been clear for some time that one cannot portray the process of creation by writing an article that describes it. The reader must have direct experience with the systems under discussion. This journal facilitates exposition that combines written material and access to software. We are interested in electronic representation and manipulation of mathematics and in factors that influence the development of software. The best way to address these matters is to discuss the development and evolution of a particular software system. I have chosen a system written for elementary group theory, Groups32, because the subject matter is familiar to most mathematicians.
I will not distinguish in this article between research and instructional systems. Groups32 is not an "instructional program" -- that is, it does not contain expository material to teach group theory. Rather, it is a research program that has been made suitable for instructional use. It provides students with a tool for experimentation. In a theoretical abstract algebra course, I have found it a good system for providing experience, examples, and experimentation.
History of Groups32
My first step in developing what came to be Groups32 was inspired by Kenneth Almquist’s electronic publication in 1989 of a set of tables for groups of orders 1-16. I wrote the first stages of the program (then Groups16) just to solve a problem stemming from an accident: Almquist's posting contained some tables that represented isomorphic groups. A natural question was to determine what one must know about groups of orders 1-16 to determine quickly whether two tables represent isomorphic groups. Eventually, Groups32 evolved into a more substantial program that now contains tables for all groups of orders 1-32 and a collection of algorithms to compute a variety of information about these groups. I developed the program using the same techniques as for several special-purpose research systems.
Evolution of a Computer Application - Forth
I have used the computer language Forth as the base language for this work because it is well suited for the task of implementing special-purpose languages and creating highly interactive mathematical systems.
It is not the purpose of this article to make readers expert in Forth. The interested reader will find a variety of resources (Forth implementations, books, tutorials, etc.). Most of this article requires the development of a reading knowledge of the language. This means that you should be able to understand the simpler code and get the flavor of the more technical code. It also means that, if you are using one of the downloadable versions, you should be able to write some simple procedures. You should be able to read lightly through the main parts of the article first and then look at the section on Forth to get background for more detailed reading.
To program in Forth you need a development system. The downloadable versions of the Groups system include Win32Forth, a high quality Forth development system written by Tom Zimmer and Andrew McKewan, which is in the public domain. It is distributed with permission of the authors. I would like to express my thanks to Tom Zimmer for making it possible to provide a development system with this article.
For the benefit of those who are trying to execute some of the examples in the articles on the downloadable systems, we have color-coded the code fragments that appear in the article.
The Color Coding Explained
- RED code is found in the 1990 version, Groups16.
- GREEN code is found in the current Groups32.
- BLUE represents code that was not in the 1990 version and did not survive to the current Groups32. For the most part, this code represents important stages in the transition.
The next section is a brief introduction to Forth. If you are using one of the programmable versions, you should try some of the examples in this section and conduct experiments to get the "hang" of the language. The section after that discusses an early version of the groups program.
The most important documentation in Forth is a glossary. Appendix A (a PDF file) is a glossary of the standard Forth words used in this article, and Appendix B (also PDF) is a glossary of the words defined in Groups32.
I suggest that you run the Groups16 (1990) program in one window while reading the article in another, and try some of the examples. The glossary should also be available for reference -- it can either be open in another window or printed.
Evolution of a Computer Application - The Forth Language -- a Brief Introduction
Forth is a language designed to create languages. It is easy to learn by understanding how it works! Unlike most conventional languages, its syntax is based on semantics: The emphasis is on what is done rather than on how it is said. The quickest way to introduce you to the process of programming is to examine and discuss some code, and that is what I will do in the remainder of the article. I start with some background information.
- The Dictionary
- Interpreting
- Seeing What Is on the Stack
- Compiling
- Terminology and Naming Convention
- Control Structures
- Data
a. The Dictionary
The Forth language is a collection of commands, which we may think of as words in a dictionary. The name for a command (which is called a "word") can be any collection of printable characters delimited by spaces. Each command has an associated action. The dictionary consists of the names and some stored representation of the action.
The process of programming in Forth consists of adding new words (and actions) to the dictionary. A glossary of standard Forth words used in this article is found in Appendix A. Individual words can be accessed using the bookmarks in Adobe Reader.
Forth maintains its dictionary in chronological (rather than alphabetical) order. The dictionary looks like a linked list: When a new word is defined, it is added at the end of the dictionary.

b. Interpreting
The Forth system has two modes. The first – interpreting – occurs when the system reads a line of input. When a word is encountered in the input stream, the dictionary is searched, starting from the most recent entry. If the word is found, its action is performed. If a word is not found, the system tries to interpret it as a number.
Since a word's action is performed when the word is encountered, any parameters it needs for its action must be already available. Thus the words (or numbers) that are used as parameters must occur before the word in the input stream. Some means must be provided for storing these parameters – a stack is used for this. By convention, most words act by removing their arguments from the stack and placing their results on the stack. (While numbers are not stored in the dictionary, they can be thought of as words whose action is to put themselves on the stack.)
Example:
3 2 +
This sequence (reading left to right) puts 3 on the stack, and then puts 2 on the stack. + is a word that takes two numbers from the stack, adds them, and puts the result (5 in this case) on the stack. Here are some examples with two operations:
3 2 + 7 * leaves 35 on the stack 3 2 7 * + leaves 17 on the stack 3 2 7 + * leaves 27 on the stack
There is no hierarchy of operations or use of parentheses to postpone operations. The sequence 3 2 7 puts these numbers on the stack (with 7 on top). The operations + and * are performed on the top two numbers on the stack.
NOTE: If you try these examples you will not see the results. The numbers on the stack are not usually displayed. Read on to find out how to see numbers on the stack.
The stack is a central feature of Forth. It (rather than named variables) is the means by which words communicate with one another. In most languages data items must be named before they can be used. A typical Forth word takes some unnamed parameters from the stack, performs some operation on them, and leaves the result(s) on the stack. The action of a word is usually documented by a "stack diagram" that shows what the word expects on the stack before it acts and what it leaves after. Often the programmer adds a further note of explanation, but sometimes this is obvious from the name chosen for the word. The stack diagram for + or * is
<p class="rteindent1>(n1 n2 – n3)which indicates that each expects two integers on the stack and leaves one integer. The names + and * indicate quite clearly what these words are intended to do.
c. Seeing what is on the stack
If you type 3 2 + (and press enter) you will not see anything! The result is on the stack, which is not visible. There are two operations that you must know about for seeing results:
d. Compiling
Programming in Forth is equivalent to adding new words to the dictionary. Here is the main way new words are added. The Forth word : (colon) is used to start a definition -- it is followed by the name of the word to be added. The definition is terminated by the Forth word ; (semicolon). The action of the : (colon) is to create a new dictionary header and switch the system to compiling mode. The action of ; (semicolon) is to compile a termination word and to return the system to the interpreting mode. The other words in the definition describe a sequence of actions to be taken when the new word executes. At the time of definition, these words do not carry out their action -- the action is stored in the new definition. (Note 1)
Example:
: 2* DUP + ;
We have chosen to name the new word 2*. The action of this word is to perform the action of DUP followed by the action of +. This adds the number on the stack to itself.
Compiling the action of component words results in a major speed increase without sacrificing the interactive nature of the language. The most time-consuming step is the search of the dictionary. The new word AddTest:
: AddTest 3 2 + DROP ;
executes 10,000,000 times in 1 second. The sequence of component words:
3 2 + DROP
takes 600 seconds to evaluate 10,000,000 times. This increase of 600x in execution speed occurs because, in interpreting mode, the dictionary must be searched each time the sequence is executed. In the compiled word, the dictionary is searched only when AddTest is compiled. Compilation is incremental: It occurs only when a new word is added and affects only the new definition. (It is neither desirable nor necessary to recompile an entire system to add a new command. Note 2) Indeed, new definitions can be made and compiled while in the midst of an interactive session. Execution speed for (compiled) Forth words is comparable to the execution speed for conventional compiled languages.
e. Terminology and Naming Convention
The words : and ; function as if they were called something like "DEFINE" and "END-DEF". (Note 3) The definition of 2* might seem clearer if we were to write
DEFINE 2* |
Make a new dictionary header with name 2* |
DUP + |
body -- describe the action of the new word |
END-DEF |
end the definition |
Forth tends to use punctuation marks as names for frequently performed operations. Typing speed is not the only reason: These punctuation marks are often used as part of a naming convention to indicate what new words do. The words : and ; are often used by programmers to suggest opening and closing something: Win32Forth has words COMMENT: and COMMENT; that are used to open and close multi-line comments.
The word . (dot), used to print the number on the top of the stack, is often used as part of the name of a word that prints something. A Forth programmer who sees a word with a dot in it will automatically assume that this word is intended to print. Later in this paper, for example, we will define a word "Set." that (as the naming convention suggests) is a word that prints a set.
It is extremely helpful, when writing Forth programs, to choose names well. A good name should suggest its action. The use of programming conventions involving the punctuation marks is also very helpful.
f. Control Structures
Forth provides control structures, such as IF .. THEN, which are like those found in most languages. IF and THEN are Forth words that are in the dictionary and, like other Forth words, they have associated actions. As noted already, most Forth words do not act during compilation -- they are, instead, compiled into the current definition. Control structures change the flow of execution and are implemented by words that carry out their action during compilation. The dictionary header for a word contains both the name of the word and some extra information about it. A word can be tagged (a so-called "immediate" word) so that its action is performed immediately, regardless of the state of the system. Because these words make changes in a dictionary entry, they are used only during compilation.
The placement of words such as IF and THEN in sentences can be best understood if one knows their action. Let A, B, and C be collections of words. We stipulate that A must leave a number on the stack -- zero is interpreted as FALSE, any non-zero number as TRUE. We do not want to execute A, B, C, in sequence -- we wish to execute B only if the result of A is TRUE. A flow diagram for this behavior is
![]()
Before B there must be a test of the number on the stack. If this number is 0 (FALSE), then we want to jump past B to the point right before C. Our source code must indicate where the test takes place and the target of the jump. The word IF compiles the conditional branching instruction, and the word THEN indicates the target.
Thus, in the definition of a new word, we write
A IF B THEN C
This will be compiled into the dictionary entry of the word to look like this:
| code for A | ?BRANCH | target_addr | code for B | code for C |
The target address is right before the code for C. IF compiles the conditional branching instruction and leaves space for the target address (which it, of course, does not know at the moment), so it leaves on the stack the location of the missing address. The word THEN occurs after B and THEN knows where it is! It also knows (because IF left the information) where it must fill in the address of where it is. So THEN fills in the proper target address -- and we are left with compiled code that looks like the diagram above.
Notice that IF and THEN do not themselves occur in the dictionary entry of the word currently being defined (although we sometimes talk as if they do). Their job is to act during compilation. Their action is to leave behind code that will, when it executes, provide the proper control flow.
The conditional branching instruction follows the convention of other Forth words: It removes the number tested (its argument) from the stack.
Example:
: ABS
DUP 0< IF NEGATE THEN ;
This word has the stack diagram ( n - n' ), where n' is the absolute value of n. The word 0< has the stack diagram ( n - t/f ), and NEGATE has the diagram ( n - n' ) with n' = -n.
ABS negates a negative number but not a non-negative number. The definition can be written up with the stack comment and additional comments:
: ABS ( n - n' )
\ n' is the negative of n
DUP 0< IF NEGATE THEN ;
Besides IF .. THEN, there are other control structures:
IF..ELSE..THEN BEGIN..UNTIL BEGIN..WHILE..REPEAT DO..LOOP
Forth does not have a separate program called "the compiler" -- the functionality of a conventional compiler is delegated to the action of the "immediate" words.
g. Data
The last thing that must be discussed in this brief introduction is how data are handled. The word : (colon) is called a defining word because it is used to add new words to the dictionary. There are other defining words that come with a Forth system, and Forth provides a mechanism for the user to make others. The defining words for data items create new words (children) in the dictionary and allocate memory for the data associated with those words. They also specify the run-time action of their children. The child word usually will put either the address of the data item or the item itself on the stack. For integer data, we use three defining words: CONSTANT, VALUE, and VARIABLE. Here is how each of these creates a new word in the dictionary:
| Example | When word is created | When word is used |
5 CONSTANT xxx |
Create a constant xxx initialized to 5 | xxx puts 5 on the stack. A constant cannot be changed once it is defined. |
5 VALUE yyy |
Create a value yyy initialized to 5 | yyy puts 5 on the stack but 7 TO yyy will change the stored value to 7. |
VARIABLE zzz |
Create a variable zzz (some implementations initialize to 0) | zzz puts the address of the storage on the stack. Words @ (fetch) and ! (store) can access and store data. |
Evolution of a Computer Application - Groups16 -- 1990 version
|
The numbering of groups in this section is different from that in later sections and in the current Groups32 program. (Some of the groups in this section are isomorphic.) |
Groups16 is an early version of the groups system. The system originated with a posting to Usenet in 1989 by Kenneth Almquist. He had generated tables for groups of orders 1-16, apparently as an exercise in combinatorics programming. In his original posting some of the tables represented isomorphic groups. Groups16 started in an effort to find out how much (or how little) one must know about groups to distinguish which tables were isomorphic.
The Almquist tables looked like this:
1 group of order 1: ___ A|A
1 group of order 2: _____ A|A B B|B A
1 group of order 3: _______ A|A B C B|B C A C|C A B
2 groups of order 4: _________ _________ A|A B C D A|A B C D B|B A D C B|B C D A C|C D A B C|C D A B D|D C B A D|D A B C
1 group of order 5: ___________ A|A B C D E B|B C D E A C|C D E A B D|D E A B C E|E A B C D
An interesting thing happened: Some readers pointed out that Almquist had posted more groups of certain orders than the literature claimed. He traced the problem to the fact that his algorithm had not detected that some of the original tables were isomorphic. A subsequent posting corrected the error. However, this raised an interesting question: How much do you need to know about a group of order 1-16 to be able to easily detect isomorphism? It is obvious that, even for groups of order 16, one does not try all possible bijective mappings to see if two groups are isomorphic. Instead, one hopes to look at properties of the groups that must be preserved under isomorphism. The original steps in the system were to represent the data in a suitable way, and to implement words that computed various information about the groups.
a. Data Representation
The original version was implemented on a computer that had only 64K of memory. The version of Forth used 16-bit integers and so could address only this much memory. The Forth system and DOS used 26K of memory -- and a nicer editor had been added to bring this to 44K. This left just 20K for the group theory system and data.
Fortunately the Forth systems commonly available at that time provided a rather clever way to use the hard disk for virtual memory. The disk was organized into 1024 byte blocks, and the system provided a word BLOCK with stack diagram ( n - addr ). Using 5 BLOCK, for example, the system would check if block 5 on the disk had already been loaded into memory. If not, it would be read from disk into a buffer. In either case, the base address of the buffer would be returned. With this scheme, one could create the illusion that a large amount of data was in memory.
For purposes of this article, I have moved the earlier code to a modern (32-bit) version of Forth on a computer that has 128 megabytes of memory. I therefore put the tables into a section of the dictionary. To make the earlier code run without rewriting, I redefined the word BLOCK to refer to parts of this section of memory.
The original tables were converted to an internal format by stripping everything except the interior squares of the tables. These were arranged sequentially by row:
AABBAABCBCACABABCDBADCCDABDCBAABCDBCDACDABDABCABCDEBCDEACDEABDEA BCEABCDABCDEFBCAEFDCABFDEDFEACBEDFBACFEDCBAABCDEFBCDEFACDEFABDEF ABCEFABCDFABCDEABCDEFGBCDEFGACDEFGABDEFGABCEFGABCDFGABCDEGABCDEF ABCDEFGHBADCFEHGCDABGHEFDCBAHGFEEFGHABCDFEHGBADCGHEFCDABHGFEDCBA etc.
This amalgamation of the group tables was put in Blocks 1-10. They were spaced so that tables did not straddle disk blocks. In order to locate a particular group, it is necessary to know the order of the group, the block in which the data are contained, and the number of bytes from the beginning of the block where the data are located. With this information we can calculate the address in memory for a particular table.
Block 0 was used to store the triples Gnum, Gblk, Goffs for each group.
0 CONSTANT IDXBLK 65 CONSTANT ID
0 VALUE GNUM 0 VALUE GORD
0 VALUE GBLK 0 VALUE GOFFS
At this point I made an important decision. Most of my computations would be for a certain group, fixed for the moment. Rather than write procedures to which I would have to pass the group number as a parameter, I designated the group of interest at the moment (given by number) as "the current group", and I wrote all procedures to refer to that current group.
My word to assign the current group is >GROUP -- it stores the group number as the value Gnum, as well as the triple mentioned above. It is therefore not necessary to go back to block 0 each time we do a group computation, nor is it necessary to re-read the table from disk for each computation. Once the current group is specified, vital information about it is read into memory.
In the current version of Groups32, all the tables are stored in memory and the word >GROUP is replaced by an appropriate version. The virtual memory scheme is not used, and it is not essential for the reader to understand how it is used. It is, however, interesting that
- there was such a mechanism for dealing with the limited memory of early computers and
- code written to use this scheme can be updated fairly easily.
Click for more information about virtual memory and the code for >GROUP.
: >GROUP ( n -- ) \ set GORD GBLK and GOFFS
DUP TO GNUM
6 * IDXBLK BLOCK + DUP @ TO GORD
2+ DUP @ TO GBLK
2+ @ TO GOFFS ;
[To run this on a 32-bit system using the original data file, the @ needs to be replaced by W@, which fetches a 16-bit value.]
We now have the group data stored, together with information needed to locate the start of a particular table. Next we want to implement multiplication - which means to locate an element in a particular row and column of the table. If we number the rows and columns from 0 to Gord-1, the entry in the i-th row and j-th column will be located i*Gord + j bytes from the start of the table.
Remember that we are storing group elements as letters A, B, C, … that a computer is representing by ASCII codes 65, 66, 67, … . If we want to multiply B and C in the current group, we must first subtract 65 (the ASCII code for "A") to get the row and column, and then compute the location of the product in the table.
: 'ELE ( ele1 ele2 – addr ) \ compute address of product
ID - SWAP ID - GORD * + \ offset from base address
GBLK BLOCK GOFFS + \ address of start of table
+ ; \ address of element
Now we can define a word to print the table of a group. We first define a word that takes two elements and returns their product:
: G* ( ele1 ele2 - ele1*ele2 )
'ELE C@ ;
Notice we have named this word G* suggesting it computes the product of two elements in a group.
: .ELE ( ele -- )
\ print element with a trailing space.
EMIT SPACE ;
 The following word produces the limits for loops over all elements in the current group.
The following word produces the limits for loops over all elements in the current group.
: GLIMITS ( -- u l )
\ loop limits to run through group
GORD ID + ID ;
: TABLE ( N -- ) >GROUP CR
2 SPACES GLIMITS
DO ." __" LOOP CR
GLIMTS DO I .ELE ." |"
GLIMITS DO J I G* .ELE LOOP CR
LOOP CR ;
You can't usually tell much about a group by looking at its table. I have found that the ability to generate tables in various formats is a useful way to transport information to other computer programs.
b. Input and Output
At this point we have a way of representing and storing the main pieces of data for the program -- the group tables. We can "install" a group as the current group. We have defined the main "group theory" word, G*, which determines multiplication in the current group. We have the output word TABLE to display the table of a given group. In some sense, the word >GROUP is an input word: It allows us to specify the number of the group currently of interest.
The next step is to develop words that compute group information by chasing around the table. We need a way to input an element of the current group. We cannot, at this moment, type "B C G*" to get the product of B and C in the current group. We could, however, type 66 67 G*. WHY? First note that G* takes two parameters that are expected to be ASCII codes of upper case letters within the range of the current group. The parameters for G* must be on the stack in advance. If we type B C G*, the system will start reading from the left and will try to find B and C as words in the dictionary. If it cannot find them, it will try to interpret them as numbers in the current base (10). So 66 67 G* will work -- and the letters won’t.
Here is what happens on the current Forth system (Win32Forth) running the original code:
8 >group ok
B C G*
Error: C is undefined
In this case, B is actually a word in the dictionary (having something to do with the editor) -- but its action is not to put 66 in the stack! On the other hand, C is neither a word in the dictionary nor a recognized number. (Note 4)
Keep in mind that G* is expecting ASCII codes for group letters. An input format that requires the user to remember and put in these codes is not friendly. There are several ways to handle the input of group letters.
Input of Elements - method 1 (using a handler)
Forth is perfectly happy to work with strings that are not names for words in the dictionary (and not numbers): We just precede them by a "handler," a word that reads a string from the following input and does something specific with it.
The Forth word ASCII (which is replaced by CHAR in the current Forth Standard) takes a following string and returns the ASCII code of its first character. In the following example we use the word . (dot) to print the number on top of the stack (and remove it).
ASCII A . 65 ASCII B . 66 ASCII b . 98 ASCII C . 67 66 EMIT B 98 EMIT b
So, for example, we could say ASCII B ASCII C G* to multiply elements B and C.
In the 1990 version, I introduced a new handler, GETE:
: GETE BL WORD 1+ C@ ;
The Forth word WORD does not take parameters from the stack -- it reads the input stream. WORD, preceded by a delimiter, takes the next string from the input stream up to the delimiter and returns the address as a counted string.
So GETE gets the next word (up to blank) and returns its first character. It is used just like ASCII but has a name that suggests that we are getting a group element.
Input of Elements - method 2 (making group elements dictionary words)
If we wish to use the simple syntax B C G* we could just make A, B, C, etc., words in the dictionary whose action is to put their ASCII codes on the stack. The easiest way to do this is to make them constants:
65 CONSTANT A 66 CONSTANT B 67 CONSTANT C 68 CONSTANT D 69 CONSTANT E 70 CONSTANT F 71 CONSTANT G 72 CONSTANT H etc.
There is a major disadvantage to this: The words I and J are the names used in Forth for loop indices. If they are redefined, they cannot be used with their original meanings. Any particular Forth implementation may already have some useful meaning attached to other letters. (Note 5)
A better approach is to use slightly different names, /A, /B, etc., for the group elements:
65 CONSTANT /A 66 CONSTANT /B
67 CONSTANT /C 68 CONSTANT /D
69 CONSTANT /E 70 CONSTANT /F
71 CONSTANT /G 72 CONSTANT /H etc.
This allows the syntax /B /C G* when typing from the keyboard.
c. Some First Procedures
: EORDER ( ele -- ord ) ID GLIMITS
DO OVER G* DUP ID =
IF 2DROP I ID - 1+ LEAVE THEN
LOOP ;
This computes the order of an element by taking powers until the identity is found.
|
Output using EORDER |
Table of group 8 for reference |
Comments for definition |
|
/A EORDER . 1
/B EORDER . 6
/C EORDER . 3
/D EORDER . 2
/F EORDER . 6
|
8 table
____________
A |A B C D E F
B |B C D E F A
C |C D E F A B
D |D E F A B C
E |E F A B C D
F |F A B C D E
|
: EORDER ID
GLIMITS DO
( x x^n )
OVER
G*
DUP ID =
IF
2DROP
I ID - 1+
LEAVE
THEN
LOOP ;
|
|
: POWERS GETE ID GLIMITS
DO DUP .ELE OVER G* DUP ID =
IF 2DROP LEAVE THEN LOOP ;
This computes and prints the powers of an element in the given group. Note that the group letter comes after the POWERS command:
POWERS A A
POWERS B A B C D E F
POWERS C A C E
POWERS D A D
POWERS E A E C
POWERS F A F E D C B
There are two groups of order 4 (numbers 4 and 5 in our list of groups). They are not isomorphic -- which can be immediately seen by computing the orders of their elements.
4 >GROUP
/A EORDER . 1
/B EORDER . 2
/C EORDER . 2
/D EORDER . 2
|
5 >GROUP
/A EORDER . 1
/B EORDER . 4
/C EORDER . 2
/D EORDER . 4
|
At this point I intended the program just to find a quick way to determine whether two groups of order 1-16 are isomorphic. An obvious step toward solving the isomorphism problem is to recognize that certain properties of a group (such as the order of the group and the order of its elements) must be preserved. It seemed useful, therefore, to write a command to loop through all elements in a group and print their orders.
Here is a very simplified version of ORDERS. In the next section we will develop fancier versions:
: ORDERS ( grp# -- ) >GROUP
GLIMITS DO I EORDER . LOOP ;
4 ORDERS 1 2 2 2
5 ORDERS 1 4 2 4
d. The Evolution of ORDERS
In this section I discuss several attempts to improve the functionality of ORDERS. The process illustrated here, where several versions of a word are produced, each improving upon the previous in some respect, is common. We always have the older version available for comparison – the system is never "broken" at any point. We try to write so that individual words can be improved without affecting other parts of the system.
The ORDERS command provides important information, but group letters may be rearranged in an isomorphism, so the orders of elements may be in a different order for two isomorphic tables. It may not be easy to see at a glance if two groups have the same number of elements of each order. It would also be much easier to compare two groups if the outputs were in a matching form. One approach would be to sort the list of orders of elements. A simpler approach, since we just want the number of elements of each order, is to define a new version of ORDERS that does book-keeping. We need an array to save the number of times each order occurs. Here we look at a way to build special types of array structures by allocating memory and producing words to access it.
I wrote the original version of Groups16 using F83, a 16-bit version of Forth (integers occupied 16 bits or 2 bytes) so a sequence of integers in memory had addresses 2 units apart. To allocate a block of memory for storage of up to 20 integers I used
CREATE OCNT 40 ALLOT
: 'OCNT ( k – addr ) 2* OCNT + ;
We need to be able to increment the number at this location:
: +OCNT ( k -- ) 'OCNT 1 SWAP +! ;
And we need to be able to initialize the array (setting all integers to zero):
: OCLEAR OCNT 40 ERASE ;
This code contains assumptions about the size of an integer and is one of the few places where modification of the code was needed when I transported it to Win32Forth for this article. Win32Forth is a 32-bit version, and addresses for consecutive integers are 4 bytes apart. The "bittedness" assumptions in the earlier code are in the use of 40 ALLOT to make space for 20 integers and in the use of 2* in the calculation of the address for a particular table entry.
What is bad about this is that one cannot update the code automatically. (Sometimes 2* is used for multiplication by 2 -- it cannot be just changed to multiplication by 4 everywhere.)
Here is a way to make the code "implementation independent": Rather than introduce "magic numbers" in the code, we introduce a word or words to contain the implementation-specific information used for allocation and address calculations. The word CELL is used to refer to the size of an integer or stack element. For F83 it has the value 2, and for Win32Forth it has the value 4. The word CELLS multiplies a number on the stack by CELL. (Note 6) With this understanding, the following definitions would work on either version of Forth:
CREATE OCNT 20 CELLS ALLOT
: 'OCNT ( k – addr ) CELLS OCNT + ;
: +OCNT ( k -- ) 'OCNT 1 SWAP +! ;
: OCLEAR OCNT 20 CELLS ERASE ;
The use of CELLS rather than 2* (which does the same in F83) has the advantage of alerting the reader to the fact that memory allocation is the issue here, rather than arithmetic. It can be useful to have different names for the same action to clarify the purpose for which the action is being taken.
We now define an improved version of ORDERS:
: ORDERS ( grp# -- ) >GROUP
OCLEAR
GLIMITS DO I EORDER +OCNT LOOP
GNUM 3 .R GORD 3 .R 2 SPACES
20 1 DO
GORD I MOD 0=
IF I 'OCNT @ . THEN
LOOP ;
There are two sections of this code, one to count the orders and the second to print the results. Notice that we print the number of elements of order k only when k is a divisor of the order of the group.
8 orders 8 6 1 1 2 2
21 orders 21 12 1 3 8 0 0 0
A slight further refinement of the output section makes it possible to produce a comma- and quote-delimited file for use in a spreadsheet. For future reference, here are words that print a comma or quotation marks, respectively:
: COMMA ASCII , EMIT ;
: QUOTES ASCII " EMIT ;
These can be used to produce "comma-delimited" output that is accepted by most spreadsheet programs. The spreadsheet file looks like this:
|
gnum |
gord |
# elements of each order |
|
1 |
1 |
" 1" |
|
2 |
2 |
" 1 1" |
|
3 |
3 |
" 1 2" |
|
4 |
4 |
" 1 3 0" |
|
5 |
4 |
" 1 1 2" |
|
6 |
5 |
" 1 4" |
|
7 |
6 |
" 1 3 2 0" |
|
8 |
6 |
" 1 1 2 2" |
|
9 |
7 |
" 1 6" |
|
10 |
8 |
" 1 7 0 0" |
|
11 |
8 |
" 1 3 4 0" |
|
12 |
8 |
" 1 5 2 0" |
|
13 |
8 |
" 1 1 6 0" |
|
14 |
8 |
" 1 1 2 4" |
The ability to export these results to a spreadsheet program (where they can be sorted and examined) proved to be a major step in identifying which of the original set of groups might be isomorphic. The number of elements of each order is preserved under isomorphism -- groups that differ in this invariant are certainly not isomorphic. We ask whether the following theorem is true:
I think most of us would regard such a theorem as unlikely. (If it were true, it would have been proved by Lagrange or Cauchy, and we would find it in textbooks.) If it is false, what is the first counter-example?
Notice that the chart above shows that up to order 8, groups are distinguished by the numbers of elements of various orders. The theorem is also true if we require the groups to be abelian. (Two abelian groups are isomorphic if and only if they have the same number of elements of each order.) For what N is the theorem true for n < N?
My last step in modifying ORDERS was to produce output in a more pleasant format.
4 orders Group number 4 of Order 4 1 elements of order 1: A 3 elements of order 2: B C D 0 elements of order 4: |
5 orders Group number 5 of Order 4 1 elements of order 1: A 1 elements of order 2: C 2 elements of order 4: B D |
Producing this output requires saving not only the count but also the order of each element. The original code, as mentioned, had built-in assumptions that integers were 16-bit. We show both the original and modified version of the code for this final version of ORDERS.
|
Original version for F83 - 24Mar90jjw |
Revised for Win32Forth |
CREATE OTABLE 40 ALLOT CREATE OCNT 40 ALLOT
: 'ORD ( ele -- addr )
ID - 2* OTABLE + ;
: 'OCNT ( i -- addr )
2* OCNT + ;
: +OCNT ( ord -- )
'OCNT 1 SWAP +! ;
: ORD! ( ord ele -- )
'ORD ! ;
: OCLEAR
OTABLE 40 ERASE
OCNT 40 ERASE ;
|
CREATE OTABLE 20 CELLS ALLOT CREATE OCNT 20 CELLS ALLOT
: 'ORD ( ele -- addr )
ID - CELLS OTABLE + ;
: 'OCNT ( i -- addr )
CELLS OCNT + ;
: +OCNT ( ord -- )
'OCNT 1 SWAP +! ;
: ORD! ( ord ele -- )
'ORD ! ;
: OCLEAR
OTABLE 20 CELLS ERASE
OCNT 20 CELLS ERASE ;
|
Using these auxiliary words, the new definition of ORDERS is
: ORDERS ( grp# -- ) CR >GROUP
." Group number " GNUM .
." of Order " GORD . CR OCLEAR
GLIMITS DO
I EORDER DUP +OCNT I ORD! LOOP
GORD 1+ 1 DO GORD I MOD 0=
IF 3 SPACES I 'OCNT @ 2 .R
." elements of order "
I 2 .R ." : "
GLIMITS DO I 'ORD @ J =
IF I .ELE THEN
LOOP CR
THEN LOOP ;
: Orders ( grp# -- ) CR >Group
." Group number " Gnum .
." of Order " Gord . CR
Calc-Orders Prt-Orders ;
e. Finding Isomorphisms
All of the groups in Almquist's list have different distributions for the orders of elements until we get to his groups of order 12. Here we find, for the first time, two groups in his list that have the same number of elements of each order.
Gnum |
Gord |
#elements of each order |
25 |
12 |
" 1 1 2 2 2 4" |
24 |
12 |
" 1 1 2 6 2 0" |
22 |
12 |
" 1 3 2 0 6 0" |
20 |
12 |
" 1 3 8 0 0 0" |
21 |
12 |
" 1 3 8 0 0 0" |
Groups #20 and #21 are, therefore, the first groups in the original set that could be isomorphic. To show that they are isomorphic, we need to display an isomorphism between them. A first attempt at displaying an isomorphism is to create a mechanism for showing what happens to a table under a mapping of elements. We imagine a mapping X that sends the letters A, B, C, … to the same letters in a permuted order.
CREATE 'XG 20 ALLOT \ This will contain the images of A,B,C,…
: XG ( ele - xele ) \ given ele this displays the image xele
ID - 'XG + C@ ;
: XG' ( xele - ele ) \ this finds the inverse image of a letter
GLIMITS DO I XG OVER =
IF DROP I LEAVE THEN LOOP ;
: XG* ( x1 x2 - x3 ) \ Multiply in image group
XG' SWAP XG' SWAP G* XG ;
: >XG ( follow by string in letters )
\ this allows input of the mapping
BL WORD COUNT 'XG SWAP CMOVE ;
: RTABLE ( n -- ) \ This prints the table of the image group
>GROUP CR
2 SPACES GLIMITS DO ." __" LOOP CR
GLIMITS DO I .ELE ." |"
GLIMITS DO J I XG* .ELE LOOP CR
LOOP CR ;
>XG ACBD |
This applies map A to A, B to C, C to B, D to D |
5 TABLE ________ A |A B C D B |B C D A C |C D A B D |D A B C |
Original table for group 5 |
_A_C_B_D A|A C B D C|C B D A B|B D A C D|D A C B |
Intermediate table obtained by interchanging B and C wherever they occur. |
5 RTABLE ________ A |A B C D B |B A D C C |C D B A D |D C A B |
Final table obtained by rearranging rows and columns |
We have applied the isomorphism X and obtained the resulting table. Can we apply an isomorphism like this to Group #20 and transform its table to that of Group #21?
There are 12! = 479,001,600 candidates for X. However, if X is an isomorphism from group 20 to group 21, it must send A to A, it must send an element of order k to an element of order k, and it must send a product in the first group to the product of the images in the second group. (In fact, the map is determined by what it does to the generators -- but we do not yet have tools to determine the generators.)
20 orders
Group number 20 of Order 12
1 elements of order 1: A
3 elements of order 2: D I K
8 elements of order 3: B C E F
G H J L
0 elements of order 4:
0 elements of order 6:
0 elements of order 12:
|
21 orders
Group number 21 of Order 12
1 elements of order 1: A
3 elements of order 2: E I K
8 elements of order 3: B C D F
G H J L
0 elements of order 4:
0 elements of order 6:
0 elements of order 12:
|
20 table ________________________ A |A B C D E F G H I J K L B |B C A E F D H I G K L J C |C A B F D E I G H L J K D |D G J A L H B F K C I E E |E H K B J I C D L A G F F |F I L C K G A E J B H D G |G J D L H A F K B I E C H |H K E J I B D L C G F A I |I L F K G C E J A H D B J |J D G H A L K B F E C I K |K E H I B J L C D F A G L |L F I G C K J A E D B H |
21 table ________________________ A |A B C D E F G H I J K L B |B C A E F D H I G K L J C |C A B F D E I G H L J K D |D I L G C K A F J B H E E |E G J H A L B D K C I F F |F H K I B J C E L A G D G |G J E A L H D K B I F C H |H K F B J I E L C G D A I |I L D C K G F J A H E B J |J E G L H A K B D F C I K |K F H J I B L C E D A G L |L D I K G C J A F E B H |
If we map B to B, then we must map C to C, since C is B*B in both groups. D must get mapped to an element of order 2. Let’s try D to E. B*D is F in Group 20, B*E is F in group 21 so we should map F to F. Continue working in this fashion.
>XG ABCEFDGHIJKL 20 RTABLE A |A B C D E F G H I J K L B |B C A E F D H I G K L J C |C A B F D E I G H L J K D |D I L G C K A F J B H E E |E G J H A L B D K C I F F |F H K I B J C E L A G D G |G J E A L H D K B I F C H |H K F B J I E L C G D A I |I L D C K G F J A H E B J |J E G L H A K B D F C I K |K F H J I B L C E D A G L |L D I K G C J A F E B H
This can be seen to be the same as the table for group 21. We have, therefore, shown that groups 20 and 21 are isomorphic by displaying an isomorphism between them.
| The ISOMORPHISM command in Groups32 developed from this idea. It is much more sophisticated: It allows the user to experiment with images of elements (undoing trials if they do not seem to work), automatically computes and fills in all consequences of a partial mapping, checks for inconsistencies, etc. |
Evolution of a Computer Application - Comments on Improvements
It is possible to criticize and improve upon almost everything done so far. While it is good to reevaluate and improve code, it has proved to be bad to do this prematurely. The first goal should be to produce something that works and to experiment with options. A working system is the most important tool for developing improved versions. The modularity of Forth-produced systems often makes it possible to revise segments of a system while retaining code that comes before and after.
It is often not possible, or even desirable, to pre-conceive a system and design it on paper before writing any code. Forth does not require this (an advantage for this type of work). It usually becomes apparent only when a system is used what parts of it need speeding up, what parts could use a more congenial nomenclature, what functions are really needed, how they should work, and what form is best for the information they produce. This approach to system design can be called "middle out" coding: A rudimentary version of a system is produced, and it is refined and expanded as it is being used.
- Changing the Language to Fit the Program
- Choosing Better Names for Words
- Inconsistent Methods of Action
- Improving Speed
- Forth Style
- Eliminating Magic Numbers
- Back to the Isomorphism Problem
a. Changing the language to fit the program
I preferred, for this article, to transport the earlier code to Win32Forth, which is used to run the current Groups32. The earlier Forth system used 16-bit integers and the current system uses 32-bit integers. In the earlier version, the group data were stored on disk using a virtual memory mechanism. In the modern version, the data are stored in memory as part of the dictionary. This change in the way data are stored did not actually require altering the code for the rest of the system - it was handled by an approach that may be unique to Forth: Instead of changing the code, change the language. We define a word BLOCK that reads data stored in a segment of memory. It appears to the rest of the code to act just as if the older virtual memory scheme was being used:
\ +++++++++++++++++++++++++++++++++++++++ \ + pseudo block structure + \ +++++++++++++++++++++++++++++++++++++++
CREATE PSEUDO 12 1024 * ALLOT
: BLOCK ( n -- addr )
1024 * PSEUDO + ;
When the program is loaded, group data are read from the original block file into this segment of memory. The rest of the program does not know that the definition of BLOCK has been given a new meaning.
b. Choosing better names for words
Now let me talk about some of the things I didn't like and that were changed. For one thing, I didn't like the names that I gave to some things in the original version. The word GLIMITS, for example, is used to put the loop limits on the stack for a loop over all elements of the current group. The etymology is obvious -- but it is a name for how the word does something rather than what it does. In use I found myself always having to look up what name I had used -- there is something not at all memorable about the name "GLIMITS". In Groups32, this has been replaced by the word "For_All_Elements". For similar reasons, the word EORDER has been replaced by EleOrder. (Note 7)
When I have used this code with others new to Forth, I found that it was helpful to distinguish words that come as part of the Forth language and those that have been added as part of the Groups package. Words that are part of Forth are typed in caps, words added for the system are in mixed case. Contrast:
: ORDERS ( grp# -- ) >GROUP
GLIMITS DO I EORDER . LOOP ;
: Orders ( grp# -- ) >Group
For-All-Elements
DO I EleOrder . LOOP ;
As I have used Forth, the importance of a good choice of names has become clear. With proper choices, one can often read a section of code without having to refresh one's memory by looking up a description of the word in a glossary or in the source code. A properly chosen name for a word can often suggest what it does.
c. Inconsistent methods of action
I also do not like inconsistencies among actions of words. To enter elements as parameters, we have several possibilities. In the code above we have words that require the ASCII code of group letters in advance -- and we introduced special words such as /A, /B, /C to allow this to be done conveniently. The word EORDER uses this approach: We say /B EORDER to get the order of B. The word POWERS, however, is based on the handler GETE. We say POWERS B to get the powers of B. Both are words that take an element of the current group as a parameter. Both approaches are valid.
I have found it confusing to have some words that take the parameter in advance, and some that take it afterwards. This practice requires that you remember this matter of placement for each word. It is better to have similar words act consistently, if possible. Words that act on elements should all either take their argument in advance or take it afterward. It is more consistent with the style of Forth to have parameters for the word occur in advance - so, eventually, I eliminated the approach based on GETE. It is easy to change the definition of POWERS to take its argument from the stack:
Syntax: POWERS B |
Syntax: /B POWERS |
: POWERS GETE ID GLIMITS
DO DUP .ELE OVER G*
DUP ID =
IF 2DROP LEAVE THEN
LOOP ;
|
: POWERS ID GLIMITS
DO DUP .ELE OVER G*
DUP ID =
IF 2DROP LEAVE THEN
LOOP ;
|
When faced with this kind of choice, it is usually not wise to spend a lot of time in meditation before writing the code. The best approach is to implement both possibilities and use them for a while before deciding the winner. (In keeping with the evolutionary theme of this article, one adopts a "survival of the fittest" approach to modifications.)
d. Improving speed
Notice that the group tables store letters A, B, C, ... for the table entries. Since finding the product of two elements involves calculating a location in memory, every use of G* involves first subtracting ID (the ASCII code for the identity) from the two letters. It should be possible to use integers 0, 1, 2, ... for the internal representations of the group elements, which would eliminate some extra calculations for G*. It does require, however, that group elements be converted to and from ASCII upon input and output. Speeding up G* (used many times within a computation) is far more important than speeding up printout (which occurs only at the end). Input and output operations occur relatively infrequently and tend to be sufficiently fast.
I should also be mention at this point that one can define selected Forth directly in assembly language. The word G* is executed very frequently, since most words in the system use it either directly or indirectly. In the following chart, I compare execution times for three different definitions for G*: the original Group16 definition (group elements stored as letters), a Groups32 version using a "high level" Forth definition, and the current Groups32 version using an assembly language definition.
The timings were obtained using the same version of Forth (Win32Forth) running on the same computer - so differences are due entirely to the way the data are represented and the way G* is coded.
|
Timing for 10,000,000 executions of G* |
|
|
Original Groups16 // table stores group letters A, B, C, … |
98420 ms |
|
Current Groups32 ver 7.0 // table stores 0, 1, 2, … |
35750 ms |
|
Same as above with G* written in assembly language |
7300 ms |
Of course, the value of trying to improve the speed of a single word depends on how much gain can be achieved, how frequently the word is used, and whether or not the additional performance is needed. If a word is used mainly interactively (i.e. a command usually issued from the keyboard) and it returns an answer in 1/10 second, it is hardly worthwhile to try to get it to execute in 1/100 second. A word like G*, however, is executed quite frequently. (Note 8)
One should check code to see if the same computation is made repeatedly and should be replaced by code that computes once and stores the result. A number can be retrieved from a table far more quickly than it can be found by looping through a list. An example of this is the word XG' (badly named) that finds the inverse of an element under a map. In order to compute the product XG*, the inverse must be found twice. In order to display the translated table (RTABLE), the product XG* must be computed for each pair of elements. It is possible to rewrite >XG (the word that stores the map) so that it computes and stores the inverses. I made improvements like this in the eventual ISOMORPHISM command in Groups32.
e. Forth Style
Groups32 is a software system that is designed to be modified and expanded as it is used. We will gradually produce a collection of "top level" commands to be used interactively. These are supported by a collection of foundational and auxiliary words.
The fact that Forth programming results in a large collection of words enhances the ability of a user to extend and modify the system. Forth style typically emphasizes the production of words with fairly short definitions. Deeply nested loops and control structures can be avoided by introducing auxiliary words. By keeping definitions short and uncomplicated, it is easier to spot errors. Equally important for system development is the fact that words can be executed interactively - one can test individual words in piecewise fashion as they are being written.
This process of breaking definitions into smaller parts is called "factoring". The most complicated word we have written so far is ORDERS:
: ORDERS ( grp# -- ) CR >GROUP ." Group number " GNUM . ." of Order " GORD . CR OCLEAR GLIMITS DO I EORDER DUP +OCNT I ORD! LOOP GORD 1+ 1 DO GORD I MOD 0= IF 3 SPACES I 'OCNT @ 2 .R ." elements of order " I 2 .R ." : " GLIMITS DO I 'ORD @ J = IF I .ELE THEN LOOP CR THEN LOOP ;
Notice that some factoring has taken place: Clearing the tables (OCLEAR), computing the order of an element (EORDER), incrementing the count (+OCNT), storing the order (ORD!), and printing an element (.ELE) have all been delegated to separate words. When writing ORDERS, we need to be able to perform these tasks, but we can forget the details of how they were performed.
It is certainly possible to factor ORDERS still further. Some Forth writers like to make the top-level word look like this:
: ORDERS ( grp# -- ) Install-Group Initialize-Tables Compute-Counts Display-Info ;
There is another reason for factoring: to separate sections of code that may be independently useful. Here is a hypothetical word that, for some reason, needs to determine if the current group is abelian. The highlighted code accomplishes this by testing whether each pair of elements commutes.
: BigWord <some stuff> |
TRUE
GLIMITS DO
GLIMITS DO
J I G* I J G* <>
IF DROP FALSE THEN
LOOP LOOP
|
|
Making this a separate word will clarify the definition of BigWord, and it will also produce a word that is potentially useful elsewhere:
: Abelian? ( -- t/f )
\ is current group abelian?
TRUE
GLIMITS DO GLIMITS DO
J I G* I J G* <>
IF DROP FALSE THEN
LOOP LOOP ;
Then we replace the code segment in BigWord by the word Abelian?
: BigWord
<some stuff>
Abelian?
<more stuff>
f. Eliminating Magic Numbers
A feature of good style in any programming language is the elimination of "magic numbers," that is, numbers that have special significance to the system or program and that appear in the code as literal numbers. Examples of magic numbers are 16 (which appears as the maximum order of a group in Groups16), or 49 (which is the number of tables in the original Almquist posting), or 20 (which is used to allot storage for arrays -- probably because it was bigger than 16 and seemed like a nice number).
It is preferable to define magic numbers as constants and use the names rather than the numbers. This has the effect of making code more readable. The reader (most often the author) does not have to wonder why a certain number appears in the code. MaxOrder more clearly indicates that (in the current system) the maximum order of a group is being used. This is preferable to using 16, which could be the maximum order of a group -- but, then again, something else. Or that may be the maximum order now, but not when the system is extended. The elimination of magic numbers is also helpful if the code is used in a different setting. In the present case, the system was eventually changed to handle groups of order up to 32 and it was transported from a Forth system with 16-bit stack elements to one with 32.
We have already discussed the use of the word CELLS. This concept (with a different name) was introduced to me by the Kitt Peak VAX-Forth. At one time Forth was used very heavily by astronomers, and Kitt Peak produced a version of Forth allowing code to be written to run, without change, on 16 and 32-bit systems. I avoided a lot of grief in converting Groups16 to Groups32 by the fact that magic numbers appeared mainly in a few low-level words.
It is wisest to write code assuming that you will want to understand it yourself in 10 years, and perhaps modify it and use it for a different purpose. Mathematicians tend to treat computer code like theorems: They prefer not to re-prove something they already have proved.
g. Back to the Isomorphism Problem
We can distinguish groups of order up to 15 by the orders of the elements. The only groups in Almquist’s list with the same set of element orders are groups 20 and 21 (of order 12), and we have found an explicit isomorphism between them.
Groups of order 16 provide the first counterexample to the hypothetical theorem. Groups 43 and 45 have the same numbers of elements of each order, but group 43 is abelian, while group 45 is not.
Further isomorphisms occur in Almquist’s tables among groups of order 16. There are also groups of order 16 that are not isomorphic but that agree in element orders and in commutativity (abelian or not). Thus we still do not have enough properties to classify groups of order 16 up to isomorphism.
Here are some additional, easily computed, properties that may be useful - I wrote them as experiments to find useful invariants. They do not appear in either Groups16 or Groups32, since they did not seem to be of lasting interest. They were, in fact, used to distinguish the original set of group tables.
Number of Commuting Pairs
Eventually (in Groups32) we compute the center of a group and can easily compute the size of the center. At this point we just run through all pairs of elements and count those pairs that commute:
: #Commuting ( grp -- n ) >GROUP
0
GLIMITS DO GLIMITS DO
J I G* I J G* =
IF 1+ THEN
LOOP LOOP ;
Number of Squares
We can define #SQUARES to count how many elements in a group are squares:
CREATE SQ 20 ALLOT
: #SQUARES ( grp# -- n ) >GROUP
SQ 20 ERASE
GLIMITS DO
I I G* ID - SQ + 1 SWAP C!
LOOP
0
20 0 DO SQ I + C@ + LOOP ;
If one actually wishes to see which elements are squares, the following word will display the squares:
: SQUARES ( grp# -- ) >GROUP
SQ 20 ERASE
GLIMITS DO
I I G* ID - SQ + 1 SWAP C!
LOOP
20 0 DO SQ I + C@
IF I ID + .ELE THEN
LOOP ;

It turns out that, at this point, we have implemented enough properties to classify groups up to order 16. Coupled with the mechanism for exhibiting isomorphisms, we can detect which of Almquist's tables are for isomorphic groups. (There are actually only 42 groups of orders 1-16 up to isomorphism.)
The following tables were found to be isomorphic: (20,21), (33,40), (36,38), (32,39,42), (34,41). In the process, I produced a method that will quickly identify any group of order 1-16 up to isomorphism.
Evolution of a Computer Application - Groups16 to Groups32 Transition
| From this point on, the numbering of groups corresponds to the intermediate revisions of Groups16 and to Groups32. The duplicate groups have been eliminated, and the numbering for groups of orders 1-16 is changed. Eventually groups of orders 17-32 will be added. |
In the transition to Groups32, I made a number of changes. ID appears so often in the code above because we stored group elements as A, B, C, … , and we often need to use the corresponding numbers 0, 1, 2, … to access tables or arrays. We have already pointed out that the group multiplication word G* would be faster if this conversion from the letters to indices were eliminated. I changed the group tables to store 0, 1, 2, ... for the elements, which required revising many of the existing words that use tables and arrays. GLIMITS (which put loop limits on the stack) was renamed to For-All-Elements, and the limits are now indices rather than ASCII codes. The words /A, /B, /C, … that put ASCII codes on the stack were changed to put 0, 1, 2, … on the stack. I changed the display word .ELE from
: .ELE ( ele -- ) EMIT SPACE ;
to
: .ELE ( ele -- ) ID + EMIT SPACE ;
| Reminder: Code in red was in the early 1990 version, Groups16; Code in green is in the current Groups32; Blue represents code that was not in the 1990 version and did not survive to Groups32. |
These changes were not as disruptive as it might seem at first. Many of the words in the system are not aware of how the data are represented and so required no change.
A consideration in implementing a system is precisely this: Can the programming be done in such a way that details of data representation are hidden in lower level words? Do most of the words in the system need to know whether group elements are represented by indices or by ASCII codes? Do most of the words in the system need to know where or how the data are stored?
These questions have repercussions when changes are made in the system. They also have psychological repercussions: How much is the mathematician allowed to think in terms of mathematical objects (groups, elements, etc.), and how much must he or she think in terms of computer representation. The purpose of some of the changes in this transition is to make the language and concepts more in terms of mathematical objects and procedures applied to them. Even the small change in name from GLIMITS to For-All-Elements is significant.
I had an important change in attitude in the transition: Several procedures were originally written to produce output on the screen -- they were regarded as top-level. I found while extending the system that it would be useful to separate the generation of information from printing it. An example of this is a factoring of the Orders command (discussed previously) into a procedure to calculate the orders of elements and a procedure to print them:
: Orders ( grp# -- ) CR >Group
." Group number " Gnum .
." of Order " Gord . CR
Calc-Orders Prt-Orders ;
This allows other commands to use information about orders of elements. This, in turn, required the development of data structures that could be used to transmit information from one procedure to another. In the case of subgroups and sets, it involved representing data in a form that could be transmitted on the stack. In the case of element orders, it meant providing other procedures access to the locations in memory where data were stored.
The transition also was marked by the addition of other features -- most notably, a way to deal with subgroups and a permutation group package -- plus refinement of existing features.
a. First Subgroups Package
My subgroups code represents a first effort to introduce some of the further structure of group theory into the system. It is transitional code and does not represent the way that subgroups are handled in Groups32. It was, however, very useful, providing a way to test later code as it was being developed. It displays the subgroup generated by a collection of elements. In the transition period, I had not yet introduced the idea of treating a set as an object that could be put on the stack.
In this package, a particular subgroup (the current subgroup) is treated as a counted table or array. This approach was eventually replaced by a more sophisticated one. While the code in this section does not appear in Groups32, it does mark an important stage in the transition.
a.i. Overview
The main purpose of this code is to find a way to exhibit the subgroup generated by a collection of elements. The subgroup being generated is represented by a counted array or table of bytes. This is a list of the elements found (so far) to be in the subgroup. The first byte is the count, and the remaining bytes are subgroup elements.
The most important top level words in the package are SGfirst ( ele -- ) and SGnext ( ele -- ), which are used to enter the first and subsequent elements. The main words used in implementation are >SGtable ( ele -- ) and SGsweep. >SGtable adds a new element to the table (subgroup) if it is not already there. SGWEEP repeatedly computes products of pairs of elements currently in the subgroup, and uses >SGtable to add the products to the subgroup. This continues until no new elements are added.
a.ii. Top Level Words and Examples
|
Top Level Words |
|
: SGfirst ( ele -- )
SG-init >SGtable
SGsweep SG. ;
|
Use this for first element to initialize the table |
: SGnext ( ele -- )
>SGtable SGsweep SG. ;
|
Use this for remaining elements |
When I first introduced these words, I was using the conventions of the 1990 version. In the 1990 system, they had a slightly different form, using GETE to get the input element from the input stream -- so one would use "SGfirst B" to start a subgroup with element B. The examples below were produced using the current version of Groups32. It is necessary to add the constants.
0 CONSTANT /A 1 CONSTANT /B
2 CONSTANT /C 3 CONSTANT /D
4 CONSTANT /E 5 CONSTANT /F
6 CONSTANT /G 7 CONSTANT /H
8 CONSTANT /I 9 CONSTANT /J
10 CONSTANT /K 11 CONSTANT /L
12 CONSTANT /M 13 CONSTANT /N
14 CONSTANT /O 15 CONSTANT /P
16 CONSTANT /Q 17 CONSTANT /R
18 CONSTANT /S 19 CONSTANT /T
The input is in the form "/B SGfirst". This output also assumes the new numbering of groups.
32 >GROUP
/B SGfirst B C D A
/E SGnext B C D A E F G H
/I SGnext B C D A E F G H I J K L M N O P
The subgroup generated by B, E, and I is the whole group.
a.iii. Details
We are storing the elements of a subgroup in SGtable. The first byte of SGtable is the number of elements already in the table. The others are the stored subgroup elements (the data) in whatever order they have been generated. Let us say we have already found that elements B, F, and E are in the subgroup and have been found in that order. The SGtable will look like this:
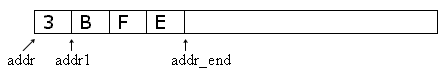
The word SGtable puts the address of the table on the stack (marked addr). The standard Forth word COUNT takes the address of a counted structure and returns the pair address_of_data and count. Thus COUNT would return the pair addr1 3 in this case. The sequence COUNT + will take addr and return addr_end (the next available position at the end of the table).
We would like to add a new element to the table if it is not already there. We use a clever (but well known) trick to do this. The strategy is to put the new element in the position at the end of the table and then scan to see if it is found. It will be found, of course.
I am torn, in this section, between clarity and authenticity. I have decided to present code in the form in which it appears in some of the transitional versions of the system. I have, however, presented the code with component sections separated by blank lines. For clarity, >SGtable should have been factored. The structure is
: >SGtable ( ele -- )
\ add ele to table if new
DUP
Put_at_end
Find_position ( pos )
Found_at_end? ( t/f )
IF Update-count THEN ;
There are obvious inefficiencies in the code: SGsweep, for example, recomputes products that have already been computed. It really should take only products with any newly added elements. Remember, however, this code is intended to display a subgroup as elements are added from the keyboard -- so its speed is really limited by the input and output.
|
Auxiliary Words |
|
CREATE SGtable 40 ALLOT
|
|
: SG. SGtable COUNT 0
?DO DUP C@ .ELE 1+ LOOP
DROP CR ;
|
Print the subgroup |
: SG@ ( k - ele[k] )
SGtable 1+ + C@ ;
|
Return the k-th element, k = 0, 1, 2, ... . |
: SG-init SGtable 40 ERASE ;
|
|
: >SGtable ( ele -- ) DUP SGtable COUNT + C! SGtable COUNT + 1+ SGtable 1+ DO ( ele ) I C@ OVER = IF DROP I LEAVE THEN LOOP SGtable COUNT + = IF SGtable C@ 1+ SGtable C! THEN ; |
Check if found at end of table (where we stored it) -- if so, increment count of table. |
: SGord ( -- sgord)
SGtable C@ ;
|
|
: SG* ( k1 k2 - prod )
SG@ SWAP SG@ SWAP G* ;
|
|
: SGsweep
SGord 0=
ABORT" Table is Empty "
BEGIN SGord
SGord 0 DO SGord 0 DO
J I SG* >SGtable
LOOP LOOP
SGord = UNTIL ;
|
Take products of existing elements in SGtable and add to table. Repeat this until no new elements are added. |
|
Top Level Words |
|
: SGfirst ( ele -- )
SG-init >SGtable
SGsweep SG. ;
|
Use this for first element to initialize the table. |
: SGnext ( ele -- )
>SGtable SGsweep SG. ;
|
Use this for remaining elements. |
b. Sets
In previous sections the top level words have printed information to the screen. The information they produced was not intended to be used by further words. In this section we introduce a representation for sets (subsets of group elements) as objects that can be transmitted to other words on the stack.
b.i. Overview
In October, 1991 I wrote a new version of Groups16, using a newer and more extensive 16-bit version of Forth (FPC). This rewrite included some of the changes above. The most notable new idea, however, was to introduce tools for representing and manipulating sets. Some of the commands could be written to produce a set as a result, rather than print a list of elements. Sets could be transmitted on the stack from one procedure to another.
Sets are represented by "bit maps": stack elements (the same as integers) in which a bit is set when an element is in the subset. For example, the set {B, D} contains elements 1 and 3 (A is element 0) and so is represented by 10, which is 1010 in binary. This allows the representation of subsets of {A, B, …. ,P}. Procedures are provided for input and output, as well as standard set manipulations, test of set membership, etc.
b.ii. Top Level Words and Examples
#Set |
( set -- #ele) | Returns number of elements in set. |
2^n |
( n -- 2^n ) | Raise 2 to the input power. (See Singleton.) |
Contains |
( set1 set2 -- f ) | Returns true if set1 contains set2. |
Empty-Set |
( -- 0 ) | Returns the empty set. |
Member! |
( ele set -- set' ) | Make ele a member of set. |
Member? |
( ele set -- f ) | Returns true if ele is a member of set. |
Set- |
( sub1 sub2 -- sub1-sub2 ) | Returns difference of sets. |
Set& |
( sub1 sub2 -- intersection ) | Returns intersection of sets. |
Set* |
( set1 set2 -- product ) | Returns the set of products of elements in set1 set2 in given group. |
Set. |
( set -- ) | Prints set (given as integer bitmap) using letters for elements. |
Set+ |
( sub1 sub2 -- union ) | Returns union of sets. |
Set-G |
( -- gset ) | Returns underlying set of current group. |
Singleton |
( n -- {n} ) | Returns set with ele as only member. |
SubGrp. |
( subg -- ;;; print subg ) | Prints subgroup (bitmap as set) using letters. This is the same as Set. |
Examples
{ ABC} { BC} Contains . -1 (true)
{ ABC} { BD} Contains . 0 (false)
/B { ABC} Member? . -1
/D { ABC} Member? . 0
/D { ABC} Member!
Set. { A B C D }
/B Singleton Set. { B }
{ ABC} { BCD} Set- Set. { A }
{ ABC} { BCD} Set+ Set. { A B C D }
{ ABC} { BCD} Set& Set. { B C }
{ ABCD} #Set . 4
8 TABLE
_A_B_C_D_E_F_
A |A B C D E F
B |B C A F D E
C |C A B E F D
D |D E F A B C
E |E F D C A B
F |F D E B C A
Group number 8 of Order 6
1 elements of order 1: A
3 elements of order 2: D E F
2 elements of order 3: B C
0 elements of order 6:
{ B} Generates Set. { A B C }
{ BD} Generates Set. { A B C D E F }
Center Set. { A }
/B Centralizer Set. { A B C }
{ B} Generates Normalizer Set. { A B C D E F }
{ D} Generates Normalizer Set. { A D }
b.iii. Details
: 2^N ( n - 2^n ) \ integer with bit n set
1 SWAP 0 ?DO 2* LOOP ;
: Singleton ( n - set ) 2^N ;
: Contains ( set1 set2 - t/f ) \ TRUE if set1 contains set2
SWAP OVER AND = ;
: Member? ( ele subg - t/f )
SWAP Singleton Contains ;
: Member! ( ele subg -- subg' )
SWAP Singleton OR ;
Notice the use of "bitwise" operations AND and OR. 5 2 OR gives 7 while 5 2 AND gives 0.
5 ( 1 0 1 )
2 ( 0 1 0 )
Here is a word for printing a set:
: SubGrp. ( subg -- ) \ print subg
." { " 1 ( bit mask )
16 0 DO 2DUP AND \ check if bit is set
IF I .ELE THEN
2* \ left shift mask
LOOP 2DROP ." } " ;
Notice that the idea of representing sets (and subgroups) as arrays has been abandoned in favor of using a representation as integers. The word SubGrp. here is defined to print a subgroup represented as an integer -- it supercedes the early version of SG. in which a set is represented as an array -- but it has the same function.
: Set. SubGrp. ;
Here is a word for inputting a set. The definition uses some features of Forth compilation to make it "state smart" (i.e., it acts differently if the system is compiling). Notice that, when interpreting, this word produces an integer, which is put on the stack. When the system is compiling, it stores the integer in the definition. This definition is not included in Groups32, since the command completion interface used there prompts for input of sets. The details of this definition are beyond the scope of this article.
: { ( -- set ;;; interpret string up to } as a set )
0 \ start with empty set
ASCII } WORD \ get string up to }
COUNT 2DUP UPPER \ convert to upper case
0 DO DUP C@ ID - DUP 0 15 BETWEEN \ check if valid
IF ROT Member! SWAP \ set addr
ELSE DROP THEN 1+ \ next address
LOOP DROP
STATE @ IF [COMPILE] LITERAL THEN ; IMMEDIATE
Some basic set operations:
: Set- ( set1 set2 -- set1-set2 )
\ set difference
OVER AND XOR ;
: Set+ ( set1 set2 -- union )
\ set union
OR ;
: Set& ( set1 set2 -- intersection )
\ set intersection
AND ;
: #Set ( set -- #ele )
0 SWAP
BEGIN ( cnt n ) DUP
WHILE 0 2 ( cnt lsb msb 2 )
UM/MOD ( cnt r n/2 )
>R + R> \ update cnt
REPEAT DROP ;
In #Set we shift bits to the right by dividing by 2. The Forth word
UM/MOD ( ud un - ur uq )
takes a double precision unsigned integer and divides by a single precision integer. It produces an unsigned remainder and unsigned quotient. In each step in the loop we are dividing by 2, the remainder (0 or 1) is added to the count, and the quotient is used in the next step.
A double precision integer is represented by two stack elements; the top of the stack is the most significant part.
An important operation on subsets of a group is to form ![]() Here is the high-level Forth version:
Here is the high-level Forth version:
VARIABLE Stemp
: Stemp! ( ele -- ) Stemp @ Member! Stemp ! ;
: Set* ( set1 set2 -- set1*set2 ) 0 Stemp !
For-All-Elements DO OVER I SWAP Member?
IF ( first ele is member of set1 )
For-All-Elements DO I OVER Member?
IF ( second ele is member of set2 )
J I G* Stemp!
THEN LOOP
THEN LOOP 2DROP Stemp @ ;
c. Sets and Subgroups
We are now in a position to write a word “Generates” that finds the subgroup generated by a given set. Notice that the idea here is the same as used previously in SGsweep: We repeatedly take all products of elements in a subgroup under construction until we get something closed under products. In this case we take only products using new elements. The subgroup is represented as a set, so adding new elements uses the set operations we have just defined. We use the following notation in the comments for Generates:
S is the originally given set of generators.
X is the total set of products formed so far.
Y is the set of products yet to be multiplied by S.
: Generates ( set -- subg ) >R
1 1 ( X = Y = {id} )
BEGIN R@ Set* ( X Y*S )
OVER Set- ( X Y' Y'=Y*S-X new prods )
SWAP OVER Set+ ( Y' X' X'=X+new )
SWAP ?DUP ( leave if no new products )
0= UNTIL
R> DROP ;
Since Set-G, the underlying set of G, occurs in subgroup operations, we have >Group calculate and save it when a new group is installed.
: LCoset ( ele subg -- lcos ) SWAP Singleton SWAP Set* ;
: RCoset ( ele subg -- rcos ) SWAP Singleton Set* ;
: Centralizer ( ele -- centrz ) 1
For-All-Elements
DO OVER I OVER G* SWAP I G* =
IF I SWAP Member! THEN
LOOP SWAP DROP ;
: Center ( -- center ) 1
For-All-Elements
DO I Centralizer Set-G =
IF I SWAP Member! THEN LOOP ;
: Normalizer ( subg -- normal ) 1
For-All-Elements
DO OVER I OVER LCoset I ROT RCoset =
IF I SWAP Member! THEN LOOP SWAP DROP ;
: Normal? ( subg - t/f )
Normalizer Set-G = ;
d. Listing Subgroups
We wish to make a list of all distinct subgroups and also maintain a list of the corresponding generators. Thus the ordered list will be indices into a table of subgroups and generators. SUBGTABLE is a record structure that holds subgroups and generators for them. The comparison function SGCOMP was chosen so that subgroups get listed in increasing size. After generating all subgroups, one can access them as an array SUBGROUP with indices 0..#SUBGROUPS-1.
Ordered Lists Package
We make use of a package for handing ordered lists that was written in 1989. Rather than exhibit the code for this package, we describe the words used here.
Note: The implementation of ORDLIST used here uses single bytes for indices and therefore can contain at most 256 indices.
ORDLIST
|
|
This is a defining word. ( i j -- -1 | 0 | 1 ) |
>LST
|
( list -- ) | Install list as the current list |
ISIN?
|
( n list - i t/f ) | Check if the element of index n is in the list. If it is, i is the position, and the flag is TRUE. If it is not on the list, then i is the place where it should be inserted. |
(INS)
|
( n i --) | Insert n at position i |
LST@
|
( i - n ) | n is the entry at position i in the current list. |
OL-EMPTY
|
( list -- ) | Empty the given list. |
An ORDLIST is paired with an array-like structure that holds the actual data. The ordered list is a list of indices of data. When we create an ordered list, we supply a comparison function.
Suppose i and j are two indices and L[i], L[j] the corresponding data. The comparison function has stack diagram
( i j -- -1 | 0 | 1 ).
-1 if L[i] < L[j], 0 if L[i] = L[j], and 1 if L[i] > L[j].
One of the uses of ordered lists in this system is to keep a list without duplicates.
In the following code, we establish an array SUBGTABLE that holds subgroups and generators. The comparison function SGCOMP compares subgroups. S1 < S2 if S1 has fewer elements than S2 or, if they have the same number of elements, S1 comes before S2 as unsigned integers. SUBGLIST is the name for the ordered list. When this name is used, an address is put on the stack. >LST uses this address to make SUBGLIST the current ordered list and all the ordered list words refer to it.
CREATE SUBTABLE 100 2* CELLS ALLOT (Note 9) : 'SUBG ( index -- addr_of_subg ) 2 CELLS * SUBTABLE + ; : 'GEN ( index -- addr_of_gen ) 'SUBG CELL + ; : SGCOMP ( idx1 idx2 -- -1|0|1 ) 'SUBG @ SWAP 'SUBG @ SWAP OVER #SET OVER #SET - ?DUP 0= IF 2DUP U< IF 2DROP 1 ELSE U> THEN ELSE >R 2DROP R> 0> IF -1 ELSE 1 THEN THEN ;
100 ORDLIST SUBGLIST SGCOMP
VARIABLE SGPTR
: >SGTABLE ( genset -- ) \ put at end
DUP 1 SGPTR +! SGPTR @ 'GEN !
GENERATES SGPTR @ 'SUBG ! ;
: NEWSUB ( ele subgidx -- )
|
NEWSUB takes an element and the index of a subgroup in SUBTABLE. It will produce a new subgroup if the element is not in the existing one. |
2DUP 'SUBG @ MEMBER?
|
|
IF 2DROP
|
if ele is in the subgroup, then drop both |
ELSE 'GEN @ MEMBER!
|
Else add the element to generating set. This returns a new generating set with the element added. |
>SGTABLE
|
>SGTABLE takes a generating set and puts it and the subgroup it generates at the end of SUBTABLE. |
SGPTR @ SUBGLIST ISIN?
|
We now check the ordered list SUBGLIST to see if this subgroup has previously appeared. |
IF DROP -1 SGPTR +!
|
If it is already there, we DROP the position (produced by ISIN?) and decrease the SGPTR - in effect, removing the subgroup from the end of the table. |
ELSE SGPTR @ SWAP
(INS) THEN
|
If it is new, we insert the index in the proper place in the ordered list SUBGLIST. |
THEN ;
|
GENERATE-SUBGROUPS repeatedly tries to add generators to existing subgroups. Notice that the inner loop is over all elements, while the outer loop is over only the indices of SUBTABLE corresponding to subgroups added in the previous pass. (Any subgroups prior to that already have been processed.)
: GENERATE-SUBGROUPS ( grp# -- )
>GROUP SUBGLIST OL-EMPTY
SUBGLIST >LST 0 SGPTR !
1 0 'SUBG ! 0 0 'GEN ! 0 0 (INS)
-1
BEGIN ( old_top ) \ previous top of SUBTABLE
1+ SGPTR @ DUP >R \ save current SGPTR value
1+ SWAP \ use only recently added subgroups
DO \ loop over subgroups
FOR-ALL-ELEMENTS
DO \ loop over elements
I J LST@ NEWSUB LOOP
LOOP
R> SGPTR @ OVER = \ compare old SGPTR with current
UNTIL ( exit when no more subgroups have been added )
DROP ;
Once the subgroups have been generated, we display them in increasing order, first ordered by size then by lexicographic order of elements.
: SHOW-SUBGROUPS
SUBGLIST >LST
CR ." * = Normal subgroup"
CR ." Generators" 25 TAB ." Subgroup"
SGPTR @ 1+ 0
DO CR I 3 .R 2 SPACES I LST@ DUP
'GEN @ SET. 25 TAB 'SUBG @
DUP NORMAL? IF 42 ELSE BL THEN EMIT SG.
LOOP CR ;
After GENERATE-SUBGROUPS, the subgroups are in an array.
: #SUBGROUPS SGPTR @ 1+ ;
: SUBGROUP ( indx -- subg or empty )
SUBGLIST >LST DUP 0 #SUBGROUPS WITHIN
IF LST@ 'SUBG @
ELSE DROP 0 THEN ;
: SUBGROUPS ( grp# -- ) GENERATE-SUBGROUPS
SHOW-SUBGROUPS ;
Example:
8 SUBGROUPS
* = Normal subgroup
Generators Subgroup
0 { } *{ A }
1 { D } { A D }
2 { E } { A E }
3 { F } { A F }
4 { B } *{ A B C }
5 { B D } *{ A B C D E F }
e. Some Simple Programs
Notice that we are developing a group theory language that can be used when we do further programming. Here are some examples of new words created using this language:
: Abelian? ( -- t/f )
\ is current group abelian?
CENTER SET-G = ;
: IsAnOrder? ( n - t/f )
\ is n the order of some element?
\ Assume CALC-ORDERS has been run
FALSE ( n flag )
MaxOrd 0 DO OVER I 'ORD @ =
IF DROP TRUE THEN
LOOP SWAP DROP ;
: Cyclic? ( grp# -- t/f )
>GROUP CALC-ORDERS
GORD IsAnOrder? ;
When put in a loop over all groups, Cyclic? allows us to identify the cyclic groups. Here are some variants on the IsAnOrder? command:
: OfOrder ( n - ele t | f )
\ find element of order n
FALSE ( n flag )
For-All-Elements
DO OVER I EleOrder =
IF 2DROP I TRUE LEAVE THEN
LOOP
DUP 0= IF SWAP DROP THEN ;
0 CONSTANT Empty-Set
: OrderN ( n -- set )
\ set of all elements of order n
Empty-Set ( n set )
For-All-Elements DO
OVER I EleOrder =
IF I SWAP Member! THEN
LOOP SWAP DROP ;
The following is an incorrect attempt to identify the dihedral groups. It looks for groups of order n that contain an element of order 2 and an element of order n/2 and that are non-abelian:
: Oops-Dihedral? ( grp# -- t/f )
>GROUP CALC-ORDERS
Abelian? NOT
2 IsAnOrder? AND
GORD 2 / IsAnOrder? AND ;
A dihedral group certainly satisfies these conditions, but some groups satisfy these conditions without being dihedral.
Here, for example, are the two non-abelian groups of order 8. One of them actually is the dihedral group, and the other is the group of quaternionic units. It should be easy to spot group 13 as the dihedral group - it has lots of reflections (elements of order 2) and only two rotations (elements of order 4). However both groups are non-abelian and have elements of order 2 and n/2.
Group number 13 of Order 8
1 elements of order 1: A
5 elements of order 2: C E F G H
2 elements of order 4: B D
0 elements of order 8:
|
Group number 14 of Order 8
1 elements of order 1: A
1 elements of order 2: C
6 elements of order 4: B D E F G H
0 elements of order 8:
|
An easy way to locate the dihedral groups in the current Groups32 system is to use the SEARCH command -- a dihedral group has two generators x and y, x is of order 2, the order of y can be left unspecified, and the relation is xy = y'x where ' denotes inverse. It is an interesting exercise at this point to try to write a word DIHEDRAL? with the stack diagram ( grp# -- t/f ) that determines if the given group is dihedral. Here is a solution:
: Dihedral? ( grp# -- t/f )
>GROUP FALSE
For-All-Elements DO
For-All-Elements DO
I EleOrder 2 =
J EleOrder Gord 2/ = AND
J I G* J G* I = AND
IF DROP TRUE THEN
LOOP LOOP ;
I will use this as an example to explore some issues in the performance of code. It is obvious that this code is not efficient in several ways:
- It runs through all pairs of elements of the group -- it should exit the double loop if it finds a pair that satisfies the conditions.
- If the first element, I, is not of order 2, it nevertheless chooses all possible second elements, J.
- There are three conditions to be tested, and they are tested in sequence -- but all three are evaluated (and combined using AND), even if the first is false.
The code, however, is direct, simple, and easily written. It has actually been optimized for clarity rather than for execution speed.
Be aware of the modern perversion that everything must run as fast as possible. Your time is valuable! This is a word that will identify, interactively, only one group for each even order -- and it will do so in less than one second. It is simply not worth the programming time required to make this particular word run faster. It may, nevertheless, be instructive to use this as an example for examining ways to increase speed.
We introduce a way to test the conjunction of conditions that stops testing when one is found to be false. Here is a way to synthesize this behavior from existing control structures.
We want to create words ?IF and ?THEN so that ?IF cccc ?THEN behaves as follows. We assume a flag on the stack. If this flag is TRUE, it is removed from the stack and cccc is executed (leaving behind a new flag). If this flag is FALSE, then cccc is not executed, and the FALSE flag is left on the stack. This is logically equivalent to the sequence IF cccc ELSE FALSE THEN.
: ?IF POSTPONE IF ; IMMEDIATE (Note 10) : ?THEN POSTPONE ELSE POSTPONE FALSE POSTPONE THEN ; IMMEDIATE
: Dihedral? ( grp# -- t/f )
>GROUP FALSE
For-All-Elements DO
For-All-Elements DO
I EleOrder 2 =
?IF J EleOrder Gord 2/ = ?THEN
?IF J I G* J G* I = ?THEN
IF DROP TRUE THEN
LOOP LOOP ;
This version of Dihedral? will now execute a condition only if the previous conditions have evaluated to TRUE. With this change it takes only 234 milliseconds to find the dihedral groups of order up to 32 rather than 411 milliseconds.
We have previously used the word LEAVE to exit prematurely from a DO .. LOOP construct. LEAVE, however, exits only from the current loop. Forth provides a word EXIT that exits from the current procedure and a word UNLOOP that discards the current loop parameters. Thus
: Dihedral? ( grp# -- t/f ) >GROUP FALSE For-All-Elements DO For-All-Elements DO I EleOrder 2 = ?IF J EleOrder Gord 2/ = ?THEN ?IF J I G* J G* I = ?THEN IF DROP TRUE UNLOOP UNLOOP EXIT (Note 11) THEN LOOP LOOP ;
Since we have gone this far, here is a version of Dihedral? that takes care of all three of the objections:
: Dihedral? ( grp# -- t/f )
>GROUP FALSE
For-All-Elements DO
I EleOrder 2 =
IF For-All-Elements DO
I EleOrder Gord 2/ =
?IF I J G* I G*
J = ?THEN
IF DROP TRUE
UNLOOP UNLOOP EXIT
THEN
LOOP
THEN
LOOP ;
I suspect that this can be written and understood only by someone who first writes one of the simpler versions. It finds all the dihedral groups up to order 32 in 213 milliseconds.
Now, if one frequently needs to determine whether a group is dihedral, there is a rather interesting further possibility: Generate results by a method that might be slow -- and then use the stored results rather than re-calculating.
CREATE DIHEDS MaxTables ALLOT
\ number of groups
: 'DIHED ( grp# -- addr )
DIHEDS + ;
: Old-Dihedral? Dihedral? ;
: Dihedral? ( grp# -- t/f )
'DIHED C@ ;
: Calc-Dihedral
DIHEDS MaxTables ERASE
For-All-Groups DO
I Old-Dihedral? I 'DIHED C!
Loop ;
Calc-Dihedral
Now the time for executing Dihedral? is reduced to .03 milliseconds, not counting the time it takes to create the table. The moral of the story is that one should first optimize for clarity and go further only if it is necessary. The Forth language does support a variety of ways to make things faster and also perhaps clearer, ranging from the ability to introduce new control constructs to the ability to store previously computed information.
f. Groups32
At this point, if you are using Windows, you should run the Groups32 program in a separate window. This will make it possible to see how the program works and to try examples. Examples can be copied and pasted from the article or a text editor to Groups32. If you want to do more extended programming, Win32Forth uses plain text files that can be created by an external editor and loaded into Groups32 by using INCLUDE
A useful Forth word is "see". SEE
Evolution of a Computer Application - Permutations
This package provides the basic representation and manipulation of permutations. It also provides a procedure for computing the group generated by a given set of permutations.
- Overview
- Top Level Words and Examples
- The Temporary Storage Problem
- Cycle Notation
- Details
- Temporary Storage
- Permutation Groups
- Bugs, Error Traps, Etc.
- Range Checking
a. Overview
A permutation is represented as an array of bytes. If P is a permutation of 1...n, byte 0 is used to store n and bytes 1...n store P(1)...P(n). A permutation is represented on the stack by the base address of this block of memory.
Access words are provided to manipulate permutations:
If P sends i to j, then i P Sends returns j. To make P send i to k, do k i P Send!.
(The order is chosen to be consistent with Forth "k addr !" to store k at addr.)
In the earliest version of this package, I used a defining word to declare a permutation and set aside storage for it. I provided words for input, output, and multiplication of permutations. Eventually I added a mechanism to deal with the storage of intermediate results to allow permutations to be used in chain computations. I also added a procedure to find the group generated by a set of permutations.
b. Top Level Words and Examples
We start with the earliest attempt. Notice that not all of these words are in the current version of Groups32. We make a defining word MakePerm that allocates a block of storage for a named permutation. We will access the storage as an array of bytes. If the permutation is understood to permute 1, … , n, we store n in byte 0. In general, byte k will contain the image of k under the permutation. The word PInit ( n perm ) initializes a permutation to be the identity. The word P. ( perm ) prints a permutation. To store a permutation, I introduced the word P! with stack diagram ( x1 .. xn n perm ), where xk is the image of k under the permutation. An initial version of a multiplication word, here called oP* ( perm1 perm2 - result ), multiplies two permutations and puts the product in a named permutation called Result.
Reminder: Code in red is found in the early 1990 version, Groups16; Code in green is found in the current Groups32; Blue is used to represent code that was not in the early version and did not survive to Groups32.
Here is how this looks in use:
MakePerm P1 \ Declare P1 and P2
MakePerm P2 \ as permutations
1 2 4 3 4 P1 P! \ Store data
2 3 4 1 4 P2 P!
P1 P. { 1 2 4 3 } \ print permutations
P2 P. { 2 3 4 1 }
P1 P2 oP* P. { 2 3 1 4 }
\ use default left->right
We eventually add input and output in cycle notation, but the most serious problem at the moment is that the definition of multiplication puts all products in the same place: a permutation named Result. The problem can be seen in this example
1 2 4 3 4 P1 P!
2 3 4 1 4 P2 P!
P1 P2 oP* DUP oP* P. { 3 1 3 4 }
The correct answer is
P1 P2 P* DUP P* P. { 3 1 2 4 }
What is happening is that the first product P1 P2 oP* is stored as the permutation Result. The sequence DUP oP* makes Result both the input and output. Since oP* alters the permutation Result, it is altering its input argument in this case. The conclusion is that for chain calculations there must be more than one place for results.
It is important to understand that this is not a problem peculiar to permutations -- it arises even for integer arithmetic. The stack provides the kind of flexible storage needed. If we perform a*b + c*d (using algebraic notation) we would do a b * c d * + (using reverse Polish notation). The result of the first multiplication must be temporarily stored until we perform the second multiplication. The stack diagrams for this sequence of operations show a*b remaining on the stack until the final addition.
c. The Temporary Storage Problem
There are several possibilities for dealing with the problem of intermediate storage. The first, and worst, is to try to put the data for a permutation on the Forth parameter stack. This approach would make a permutation occupy several stack cells. It has the effect of burying useful data and inhibiting the use of the standard stack operations.
A second, more promising, approach is to create a special permutation stack. Since the same problem of intermediate storage arises with other types of algebraic objects, and since a system might have several types of objects, this would require the user to introduce a new set of stack operations for each stack, and to be aware of the contents of several stacks while programming. This approach is psychologically burdensome.
In Groups32 and other algebra systems I have produced, I have represented objects on the regular Forth stack by an address. The address occupies a single cell -- so it is manipulated by the usual stack operations. The user can think of a permutation being on the stack. SWAP can be used to exchange two objects: two permutations, a permutation and an integer, etc. Thus, representing an object by its address allows a consistent way to integrate new types of data into the system. However, we still need to have a pool of locations for intermediate results.
An improved multiplication word, P*, will remove two (addresses of) permutations from the stack and multiply them. It will then put the result in the next available temporary storage location and return the address of this location to the stack.
In some languages, a very large pool of temporary locations is available -- and computation proceeds, using these locations, until the pool is exhausted. The system then attempts to identify storage locations that are no longer in active use. Unreferenced locations are called "garbage" and the process of reclaiming them is called "garbage collection". There can be a noticeable pause in execution while the system collects garbage.
We use a mechanism with storage for just 16 temporary objects. It does a very small, quick garbage collection when these are exhausted. Each type of object has its own pool of 16 storage locations. A mechanism is provided for marking an address as available. When a computation is performed on a certain type of object, the result is placed in the next available storage location, and the address is returned to the stack. If no location is available, the system tries to find which locations are no longer in active use.
d. Cycle Notation
The output word C. uses the same naïve algorithm that one uses for computing products by hand. We keep track of which numbers have already been output. Start with all numbers unmarked, and mark any element that is sent to itself. Then start with the first unmarked element. Print an opening parenthesis, print (and mark) the elements in its orbit, and print a closing parenthesis.
The input word (which I have called Perm:) reads from the rest of the command line. It is based on a word that reads a cycle (numbers between two parentheses), and it multiplies the cycles it obtains. The cycles are not required to be disjoint. Perm: does check the syntax -- so it reports errors such as improperly matched parentheses.
Perm: (1 2) (1 3)
C. (1 2 3 )
Perm: (( 1 2) (1 3
Syntax Error -- Try Again
? (1 2)(1 3)
C. (1 2 3 )
e. Details
33 CONSTANT PMaxSize \ largest n for permutations +1 for count
: MakePERM CREATE PmaxSize ALLOT ;
: 'Element ( i perm -- addr ) + ;
: Send! ( k i perm -- )
'Element C! ;
: Sends ( i perm -- perm[i] )
'Element C@ ;
: Degree ( perm -- n )
0 SWAP Sends;
: Degree! ( n perm -- )
0 SWAP Send! ;
: PInit ( n perm -- )
2DUP 0 SWAP Send! SWAP 1+ 1
?DO I DUP 2 PICK Send! LOOP
DROP ;
: P. ( perm -- )
\ print showing images of 1..n
." { " DUP Degree 1+ 1
DO I OVER Sends . LOOP
DROP ." }" CR ;
: P! ( x1 .. xn n perm -- )
2DUP Degree!
1 ROT DO I OVER
>R SWAP Send! R>
-1 +LOOP DROP ;
DEFER Direction MakePERM Result
: oP* ( perm1 perm2 -- result )
Direction
DUP Degree
DUP Result Degree! 1+ 1
DO ( perm2 perm1 )
I 2 PICK Sends ( perm2 perm1 perm2[I] )
OVER Sends ( perm2 perm1 perm1[perm2[I]] )
I Result Send!
LOOP 2DROP Result ;
: Left->Right ['] NOOP IS Direction ;
: Right->Left ['] SWAP IS Direction ;
Left->Right \ default
Recall that the multiplication operation defined here puts the product in a fixed permutation called Result and returns the address of that location to the stack. This code allows for the fact that some books use left to right multiplication while others use right to left. Forth allows for "vectored execution" using the word DEFER. The line "DEFER Direction" makes a dictionary entry for Direction, which can then be used in subsequent code. An action for Direction must be filled in before it is used. The code is written so that multiplication would be left to right without Direction (so we fill in the action NOOP when this is the desired direction). If multiplication from right to left is desired, the action for Direction is SWAP. The words Left->Right and Right->Left allow the direction to be switched without recompiling.
f. Temporary Storage
The user must understand that these temporary locations are a scratchpad area for operations on the objects - any result of lasting use must be moved to a permanent location. The garbage collector assumes that an address is being actively used if and only if it is on the stack. The internal workings of the temporary storage module are transparent to the user. In the following table I show how the mechanism is introduced into the permutations package.
Temp-Storage Perm-Temps
|
Establish a new Temp-Storage structure called Perm-Temps. |
CREATE Perm-Storage
PMaxSize CELLS 16 *
ALLOT
|
Make a block of memory to store 16 permutations. |
: Perm-Setup
Perm-Storage Perm-Temps
16 0 DO DUP I Address !
PMaxSize CELLS +
LOOP DROP ;
|
Initialize Perm-Temps to contain the 16 addresses in the storage pool. |
Perm-Setup
|
Execute the setup. |
: PTemp ( -- perm )
Perm-Temps Temp ;
|
This is the main word that the user employs - it returns the address for the next available slot in the storage pool. |
With this storage mechanism, it is very easy to fix P* without drastically changing the code. We need only to supply RESULT with the address of the next available location in the storage pool. Notice that RESULT may be used in several places in the code for an operation, and we do not want to use a different storage location at each reference. We therefore make RESULT a VALUE (rather than a permutation). It will return the address of the storage area for a permutation. We define a word GetRes to store the address of the next temporary storage slot in RESULT.
0 VALUE Result
: GetRes PTemp TO Result ;
: P* ( perm1 perm2 -- result )
Direction
GetRes DUP Degree
DUP Result Degree! 1+ 1
DO ( perm2 perm1 )
I 2 PICK Sends ( perm2 perm1 perm2[I])
OVER Sends
( perm2 perm1 perm1[perm2[I]] )
I Result Send!
LOOP 2DROP Result ;
g. Permutation Groups
The main remaining interesting feature of the permutations package is the ability to find the group generated by a given set of permutations. The algorithm for doing this is to maintain an array of the generating permutations (Gtable) and an array of permutations generated (Ptable). We use the ordered list module, discussed previously, to make the latter array an ordered list. Start with just the identity permutation in the Ptable. Repeatedly multiply all elements in the Ptable by the generators -- adding any permutation to the Ptable that is not already there. Continue doing this until a pass (multiplying by generators) does not produce anything new.
The following example shows how this feature is used from the command line. I should mention that I eventually equip Groups32 with a user interface that makes it easier and quicker to use.
\ Klein's 4-group
4 Size! \ This initializes the tables
Gen: (1 2) \ add the generators
Gen: (3 4)
Make-Group \ apply the algorithm
Show-Table \ a multiplication table can be obtained
A B C D
B A D C
C D A B
D C B A
Show-Elements
Group is of order 4
A () B (3 4 ) C (1 2 )
D (1 2 )(3 4 )
At the moment, the permutations package seems disjoint from the rest of Groups32. We cannot immediately apply any of the procedures for orders, subgroups, etc. We can, however, generate a table. We now provide a mechanism for installing this table into the Groups32 system -- replacing any of the tables 1-5 (which are for very small groups and will hardly be missed).
: Install0 \ Install as table 0
GSize @ Gord!
GSize @ 0
DO GSize @ 0
DO J I PG* J I G*! LOOP
LOOP ;
If the order of the generated permutation group is between 1 and 32, we automatically have the table stored as table 0. (The slot for group #0 is used for temporary storage.)
Groups32 provides the word Install ( n -- ), which will move the table from slot 0 to replace table n, where n is 1, 2, 3, 4, or 5. Once a table is installed, all the commands can be applied to it.
Assume the Klein 4 group is generated as above.
Install0 \ move the current permgroup to slot
1 Install \ install as group 1
1 Table \ show the table
_A_B_C_D_
A |A B C D
B |B A D C
C |C D A B
D |D C B A
1 Subgroups \ show the subgroups
* = Normal subgroup
Generators Subgroup
0 { } *{ A }
1 { B } *{ A B }
2 { C } *{ A C }
3 { D } *{ A D }
4 { B C } *{ A B C D }
Since Show-Elements provides a concordance of letters A, B, C, … with permutations, it is easy to interpret any results in terms of permutations.
h. Bugs, Error Traps, Etc.
This is an appropriate place to discuss these issues, since I eventually equipped the permutations package with error handling at the point when I first made it available for use by others. I added the error trapping even before I equipped the system with the user interface that I discuss in the next section. The permutation package was not part of the original Groups16 -- it was developed separately and eventually merged into the group theory package.
When a system of this type is used by the person who wrote and implemented it, it is usually possible to minimize "bugs" that arise from coding errors (or from disagreements between the programmer and computer about how the world works). Let us call these "bugs of the first kind". Forth style emphasizes writing short, uncomplicated definitions. Words can be tested interactively as soon as they are written. It can be quickly determined if a word does not function as intended, and the mistake is usually quickly pinpointed.
When a piece of software is used by others, however, another type of bug can appear: improper behavior resulting from incorrect use of the system. We will call these "bugs of the second kind". (Some call these "features".)
A perfect example of a "bug of the second kind" occurs in the earliest version of Groups16. Recall the definition of G*:
: 'ELE ( ele1 ele2 - addr ) \ compute address of product
ID - SWAP ID - GORD * + \ offset from base address
GBLK BLOCK GOFFS + \ address of start of table
+ ; \ address of element
: G* ( ele1 ele2 - ele1*ele2 )
'ELE C@ ;
(ID is a constant, 65, the ASCII code of upper case A.) Group elements are represented in this version by upper case letters. The code assumes that the elements are entered as ASCII codes of upper case letters -- within the range of the particular group.
4 Table ________ A |A B C D B |B A D C C |C D A B D |D C B A |
: Try GETE GETE G* ." = " EMIT ;
Try B C = D
Try b c = A
Try E F = C
|
When we put in B and C as uppercase, we get the correct answer. This word, however, is case sensitive. When we put in b and c as lowercase, we do not get the correct answer. We also get an answer when we put in E and F, even though they do not represent letters in the range of this group.
There is no "bug of the first kind" in the definition of G*. When G* is supplied with valid input it does provide the correct output. However, the code for G* contains some assumptions about how it is to be used -- and it contains no error traps to ensure it is used correctly. The errors seen here arise because G* was used incorrectly. This is a "bug of the second kind".
When the author is the user, he or she knows the intended form of input. It can be difficult for the author to anticipate some of the things other users might do -- or how the software will respond. In the user interface (Page 10), I have tried to restrict "free form" input so that Groups32 can be used correctly by those unfamiliar with the system. The input for most commands is prompted, and it is easy to test if the input is of the proper type. For example, if the user must enter the number of a group, it is easy to check that the input is a number between 1 and 144. If the user is to put in group elements, it is easy to check whether they are valid. (We automatically convert to upper case -- making the input case insensitive -- but we do check for range.) These are cases where it is rather simple and quick to insure valid input. Many bugs of the second kind can be eliminated by prompting for input in a restricted form and rejecting invalid input.
In some cases, however, we want users to provide input as a line of text -- an example is the word Perm: in the permutations package. This word is supposed to be supplied with a string that represents a collection of cycles in the numbers 1...n, where n has been specified in advance.
Left->Right 3 TO PSize Perm: (1 2)(1 3) C. (1 2 3 )
Here is an early version of code for Perm: (the names of support words have been changed to correspond to the current ones).
: 'Element ( i perm -- addr ) + ;
: Send! ( k i perm -- ) 'Element C! ;
: Sends ( i perm -- perm[i] )
'Element C@ ;
: Degree ( perm -- n ) 0 SWAP Sends ;
: Degree! ( n perm -- ) 0 SWAP Send! ;
: PInit ( n perm -- ) 2DUP 0 SWAP Send!
SWAP 1+ 1
DO I DUP 2 PICK Send! LOOP DROP ;
VARIABLE SvDepth 0 VALUE Result
: GetRes PTemp TO Result ;
: P* ( perm1 perm2 -- result )
GetRes DUP Degree
DUP Result Degree! 1+ 1
DO I 2 PICK Sends OVER Sends
I Result Send!
LOOP 2DROP Result ;
5 VALUE PSize
: << GetRes PSize Result PInit
DEPTH SvDepth ! ;
: >> DUP >R DEPTH SvDepth @ - 1
DO OVER Result Send! LOOP
R> Result Send! Result ;
: Perm:
\ use single parentheses in following string
PTemp PSize OVER PInit
BEGIN <<
ASCII ( PARSE 2DROP
ASCII ) PARSE EVALUATE
DEPTH SvDepth @ - WHILE
>> P* REPEAT ;
The size of a permutation (the n in Sn) is assumed to be in the VALUE PSize. The words << and >> are used for input of a single cycle. Here is what happens when we type << 1 2 3 >>:
The word << saves the current depth of the stack and initializes a new temporary permutation (called Result). The numbers 1 2 3 are just put on the stack. The word >> compares the stored stack depth to the new stack depth, thus determining how many numbers are on the stack. A copy of the top number on the stack is saved on the return stack and a loop is entered that makes each number the image (under the permutation) of the number below it: 2 goes to 3, 1 goes to 2. The loop is completed by making 3 go to 1. This is how a cycle is handled.
The word Perm: reads the input that follows it (presumably containing one or more cycles). It uses the << .. >> pair to interpret each cycle, and it multiplies the cycles it receives. Perm: ends its work when the input line is exhausted.
This code functions correctly as described -- as long as the user understands the assumptions built into Perm:
- There must be a space between Perm: and the rest of the input line.
- Perm: must be followed on the input line by a collection of cycles.
- There must not be anything else on the input line.
- Each cycle must begin with an opening parenthesis "(" and terminated with a closing parenthesis ")".
- Within each cycle there must be numbers in the range 1...n.
- PSize must be set to n before Perm: is used.
- The numbers within a cycle must be separated by spaces.
- The numbers within a cycle must be distinct.
- No characters, other than digits and spaces, can occur between the parentheses.
Now, what happens if a user supplies Perm: with illegal input? Suppose the user does not close parentheses, does not match parentheses, or puts illegal characters within parentheses? The system could react in several ways, ranging from aborting the command to producing something that is not a permutation, and that is handled improperly by P*, C., and other words in the package.
In the first example above, with G*, invalid input produced incorrect answers because numbers are fetched from the wrong part of memory. No damage is caused, just incorrect results. Some words, however, store things in memory, and it is possible that incorrect input could actually alter the code in memory. When Perm: is executed, the word Send! is ultimately called. This word has the stack diagram ( k i perm -- ). It will store k in the memory position of index i in the given permutation. If i is not in the proper range, a number will be stored in memory other than within the allocated space for the permutation. If k is not within range, the result will not be a valid permutation, and subsequent operations may lead to numbers being stored in improper places. Since Forth implementations usually allocate data storage within the dictionary, it could turn out that numbers can be erroneously stored in places being used by code -- and the code will, therefore, stop operating correctly.
This should not be taken as an indication of fragility. In most cases, words that store things receive their arguments from other words that produce only valid input for them.
The final versions of Perm: and its auxiliary words enforce the requirements for a correctly formed input string. The input string is checked for balanced parentheses and for only digits within the parentheses. A range-checked version of Send! is used to make sure the numbers in a cycle are within range and that they are distinct. Within the command completion interface (see Page 10), Perm: is used in a prompted input sequence, so the user must specify n first. (The word that stores n also checks that it is within range.) All of this is necessary just to try to eliminate bugs of the second kind.
i. Range Checking
Any operation that stores data in memory could, if given erroneous input, store data in unintended places. To guard against this, one can add range checking to words that store data. Here is an example from code we have already examined.
In the word Orders there is a word +Ocnt that increments the number in a certain slot in an array. Here is the original version:
CREATE OCNT 33 CELLS ALLOT : 'OCNT ( k - addr ) CELLS OCNT + ; : +OCNT ( k -- ) 'OCNT 1 SWAP +! ;
Notice that k must be in the range 0-32 for this to work correctly. Now here is a version that checks that k is in range:
CREATE OCNT 33 CELLS ALLOT
: 'OCNT ( k - addr ) CELLS OCNT + ;
: +OCNT ( k -- )
DUP 0 32 BETWEEN NOT
IF CR . ." Out of Range " ABORT
ELSE 'OCNT 1 SWAP +! THEN ;
There is, of course, a speed penalty for this extra checking. The original +OCNT executes 100,000 times in 26 milliseconds, while the range-checked version takes 50 milliseconds. The ranged checked version is twice as slow.
Should range-checking be included?
Range checking is obviously not necessary if a word is supplied its parameters only by other words that are guaranteed to supply valid parameters. +OCNT is a perfect example. This is a word that should NOT include range checking.
To see this, we need to look at how +OCNT is used. +OCNT occurs in the code for Orders, which calculates the orders of elements for one of the existing groups (of order 1-32). Thus, in use, the word +OCNT cannot receive an out-of-range index. If we were to use the range-checked version, the number k would be checked each time to see if it is between 0 and 32, but the test will always be true because +OCNT will never receive a k that does not satisfy this condition.
One of the virtues of producing software for your own use is that it is not so necessary to deal with bugs of the second kind (and with error trapping). It can be very time-consuming to prepare a piece of software for use by others. Those who have lived with toddlers will appreciate that it is very much like "child proofing" a house. How much you have to do depends both on the complexity of your house and the sophistication of your toddler. Rather than put all your possessions in locked cabinets, however, you must give thought to what precautions are really most effective.
The critical words to consider for range checking (or other error trapping) are words such as Perm: that get input from the user and store things in memory. These are the words that have the potential to alter the code itself. In the final version of the permutations package, I not only use a range-checked version of Send! but I also include other tests to make sure that the input string has the correct form.
At the beginning of the preceding section, we used the example of G*. It would not be efficient to put range checking into a word like this, which is used very frequently. It would be better to examine the code that passes information to such words, making sure that G* will not receive invalid input. Once the internal code of the system is correct, the only source of invalid data will be input routines. This is usually the best place to put error traps. Since data entry is slow anyhow, error traps here will not significantly slow the system. Once we are sure that the input routines will not send incorrect data to the rest of the system, it should not be necessary to have error traps on lower level words.
Evolution of a Computer Application - Search
Groups32 has a mechanism to search the groups of orders 1-32 to find those with given generators satisfying given relations, or to find groups that contain subgroups with the given finite presentation. The algorithm used is quite literal: All group elements are substituted for the generators, and then the orders and relations are checked. A "shortcut" evaluation is used: Once a condition is found to be FALSE, no subsequent conditions are checked.
This is the slowest procedure in Groups32. Direct assembly language coding of G* (and 8 other words) does result in a dramatic speedup of SEARCH.
Here is how SEARCH can be used to identify the dihedral groups, which are groups with two generators, x and y, with x of order 2, but the order of y is not specified. The defining relation is xy = y'x, where ' indicates inverse. The prompted input in the following example is from the command completion user interface that I describe in the next section.
Enter distinct generators as a string
e.g. RS means two generators R and S
Generators: xyDo you want these to generate the entire group? (y or n) Y
Enter the exact order for each generator.
Press Enter for no order specified
X is of order 2 Y is of order
A relation is of the form LHS = RHS
Put in LHS RHS or LHS ( if RHS is e )
LHS RHS >> xy y'xGenerators:
XY
Orders:
X= 2
RELATIONS:
XY = Y'X
-- Pressing ESC will abort the search --
2 group order = 2 X = B Y = B
5 group order = 4 X = C Y = B
8 group order = 6 X = D Y = B
13 group order = 8 X = E Y = B
18 group order = 10 X = F Y = B
22 group order = 12 X = G Y = B
27 group order = 14 X = H Y = B
40 group order = 16 X = I Y = B
47 group order = 18 X = J Y = B
52 group order = 20 X = K Y = B
58 group order = 22 X = L Y = B
69 group order = 24 X = M Y = B
78 group order = 26 X = N Y = B
86 group order = 28 X = O Y = B
92 group order = 30 X = P Y = B
111 group order = 32 X = B Y = D
The group of quaternionic units (order 8) can be presented as a group with three generators, a, b, c, and relations ab = c, bc = a, ca = b. The following chart shows the timing for the SEARCH command using different Forth implementations and computers.
|
Timing for Search |
|
|
Groups32 ver 7.0 // Win32Forth high level |
1308270 ms |
|
Groups32 ver 7.0 // Win32Forth assembly language |
51300 ms |
|
Groups32 ver 7.0 // SwiftForth |
307656 ms |
|
Groups32 ver 6.4g // Gforth LINUX |
1794000 ms |
|
Groups32 ver 6.4g // Gforth on Internet |
2700000 ms |
The entry marked Win32Forth assembly language replaces just nine words by assembly language equivalents -- the increase in speed is remarkable.
The entries for Gforth compare a LINUX version of Forth on a personal computer with the timing for the same version (running on a SUN server) accessed via Telnet on the Internet.
Notice that the fastest timing (about 1 min) is for a personal computer using assembly language coding of a few time-critical commands, and the slowest, using the Internet, is about 45 min. With the exception of the entry marked "Internet", the computer used has a Pentium III processor running at 450 Mhz.
The process of searching through a collection of groups to find those with a given set of generators and relations is inherently time-consuming. This does not preclude the possibility that a better algorithm will make a major improvement.
Evolution of a Computer Application - User Interface
When I first circulated Groups16 for review as an illustration of programming methodology, several reviewers suggested that it might make a good instructional program -- provided it could be made easier for students to use.
Groups32, as presented so far, requires the user to learn a collection of command names, together with the parameters (and order) required for their use. As with similar research systems, there are actually only a handful of top-level commands in the system. (The others are useful mainly for those who wish to write programs to extend the system.) It is not unrealistic to use the system with a "command line" interface, but there is a learning curve involved, making casual use more difficult. Typing commands and their arguments is slow. Also, a more constrained type of input would decrease the need for error trapping.
I explored several methods to make these top-level commands more accessible and to ensure valid input. In one attempt, evoking a top level command provided prompts for parameters. In another, I presented the top-level commands in a menu -- clicking on a command initiated a prompt for input.
The approach I finally used, a "command completion" interface, appears to be the quickest and easiest to use. In this interface, the user is presented with a list of available commands:
CENTER CENTRALIZER CHART CONJ-CLS COSETS EVALUATE GENERATE GROUP HELP ISOMORPHISM LEFT MENU NORMALIZER ORDERS PERMGRPS POWERS QUIT RESULT RIGHT SEARCH STOP SUBGROUPS TABLE
The user types enough letters of a command to distinguish it from the others. To generate a table, for example, the user needs only to type "T", since this is the only command that starts with T. To obtain a list of conjugacy classes, the user types "CON". The interface discards all letters typed beyond the bare minimum (so the user need not worry about mistyping subsequent characters). Once the interface identifies a command, it prints the rest of the command and prompts for any arguments needed to carry out its operation.
G1>> CONJ-CLS Group Number 8 { A } { B C } { D E F }
Typing "CON" distinguishes the CONJ-CLS command and asks for a group number.
Here is a sketch of how I implemented the interface:
The commands and information about them are put into a binary tree. Each node in the tree has a name field (for a string of a maximum size), the address of the node to the left, the address of the node to the right, and the execution address of the word used to carry out the command.
32 CONSTANT Max#Cmds
24 CONSTANT CmdSize
0 VALUE #Cmds
CmdSize CELL + CONSTANT EntrySize
Max#Cmds CONSTANT #Nodes
CREATE 'Tree1 #Nodes NodeSZ * ALLOT ALIGN
: Left ( n_addr -- l_addr ) SZ + @ ;
: Right ( n_addr -- r_addr )
SZ + 1 CELLS + @ ;
: Exec ( n_addr -- )
SZ + 2 CELLS + @ EXECUTE ;
: Left! ( x n_addr -- ) SZ + ! ;
: Right! ( x n_addr -- )
SZ + 1 CELLS + ! ;
: Exec! ( e_addr n_addr -- )
SZ + 2 CELLS + ! ;
: Name! ( $ n_addr -- ) DUP SZ BLANK $!! ;
: Leaf? ( n_addr -- flag )
DUP Right 0= SWAP Left 0= AND ;
Each new command is added to the tree to the left of an existing node if the name comes before in lexicographic order, and to the right if the command comes after. The commands are introduced by the word >CMD, which is used in the form
>CMD <menu_name> <word_to_execute>
The word_to_execute contains prompts and input routines to get any parameters needed from the keyboard. There is also a provision for including descriptive "help" information that will be printed if the user types HELP before typing the name on the menu.
Here is an example of how the Table command is made into a word %Table that prompts for input:
: %Table
Help:
This prints a table for the group requested
(and makes that the current group). Elements
are represented by letters A to Z and the
symbols [ ] ^ _ and `
Help;
." for " ['] Get-Grp CATCH 0=
IF CR Table THEN ;
>CMD TABLE %Table
I have written a collection of input commands. For example, Get-Grp is the command to get a group number. In all cases, the system waits for the user to type a string, which is put into the terminal input buffer (TIB) as if it had been typed at the keyboard in an interactive session. The input is then processed by Forth words that read the input stream. Also, the cursor position is saved at the start of input, and the cursor is returned to this position if there is an error in the input.
Here are other input commands that can be used for writing the prompted input sections.
2VARIABLE Save-Pos
: Get-TIB ( -- ) AT? QUERY AT
>IN @ 0 WORD
COUNT TYPE >IN ! ;
: Get-Num ( -- n ) ." Number " AT?
Save-Pos 2!
BEGIN Save-Pos 2@ AT
Get-TIB BL WORD
COUNT ?DUP 0= THROW
NUMBER? IF DROP TRUE
ELSE 2DROP BEEP FALSE
THEN
UNTIL ;
: Get-Grp ( -- n ) ." Group "
BEGIN ['] Get-Num CATCH
IF TRUE THROW
ELSE G-OK
DUP 0= IF CR 10 SPACES THEN
THEN
UNTIL ;
: Get-Set ( -- set )
." set: { " Get-TIB ." }"
0 0 WORD COUNT 2DUP UPPER 0
?DO DUP C@ ID -
DUP 0 MaxOrd 1- BETWEEN
IF ROT Member! SWAP
ELSE DROP THEN
1+
LOOP DROP ;
: Get-Ele ( -- ele ) ." element "
0 BEGIN
DROP KEY UPC ID -
DUP 0 Gord 1- BETWEEN
DUP 0= IF BEEP THEN
UNTIL ;
: Get-Ele. ( -- ele ) Get-Ele DUP .Ele ;
Here is how the interface works. The characters typed by the user are added to an incomplete command string. Each time a character is added, the tree is searched to see if the string matches the leading part of a name in the tree. If there is no match, the user is informed (by a beep), and the latest character is not accepted. If there are multiple matches, the system waits for further characters. If there is only one match, the remainder of the name is typed and the stored command is executed.
Since the user must type additional information from the keyboard, this interface has proved to be faster than one in which the user selects commands with a mouse. An additional feature of the interface is that it is very easy to add additional commands -- so the interface is extensible.
It is easy to learn to use the interface, and no programming is required. As a result, Groups32 can be easily integrated into courses in abstract algebra.
The original version of the interface used a single ordered list of commands. In later revisions I used a single binary tree. When I added permutations, I revised the code for the interface to enable using more than one tree. In Groups32 the permutation commands are in a second tree and there is a separate menu:
CREATE ELEMENTS HELP INSTALL MAIN MENU MULTIPLY QUIT
The PERMGRPS command in the main menu switches to this package, and the command MAIN here switches back to the main system.
Evolution of a Computer Application - Maintaining and Extending the System
| Since a Forth application is extensible and Forth compiles incrementally, it is neither necessary nor desirable to make modifications or extensions by revising and recompiling the entire system. |
I emphasize this point because it is different from the situation that arises with conventional compiled languages.
It has been found best, once a basic system is in place, to treat it as the implementation of a language: The language should be documented and not frequently subjected to total revision. Additions and modifications can be made as extensions to the existing system.
Most Forth implementations, including Win32Forth, have a provision to "save the system". The result is an executable that combines the underlying Forth system with the extensions added by the user. The combined system is then used as if Forth came with the user's words.
When I have used Groups32 for instruction, I have installed the executable on a file server, and the basic system is unchanged once installed. It is nevertheless possible to make changes and additions as the course progresses: Win32Forth reads a configuration file after the system is loaded. (Groups32 is saved as an executable with the configuration file designated Groups32.cfg.)
The line
INCLUDEupdates.f
is placed in the configuration file. The file "updates.f" is placed in a public directory, and the instructor has read/write privileges. All extensions, modifications, bug fixes, etc. are made in the file updates.f.
a. Extensions
Additions to the system can be made easily in updates.f. For some classes I have added, for example, an additional package with number theory commands. Additional commands can be added easily to the menu in the commands completion interface. First create a version of the new command that prompts for its arguments and contains help information, then install it on the menu by
>CMD <menu_name><command_name>.
If this is done in updates.f, the new command will appear on the menu whenever the system is loaded.
b. Redefining Words
It is sometimes desirable to change the action of an existing word. If a word is redefined (i.e., a new definition is made using the same name as a previously defined word), the new word is added to the end of the dictionary, and a dictionary search will find it first. Subsequent use of the name will find the new definition, but any word compiled with the older definition will continue to use the older action.
If >CMD is used with the new action, the command completion interface will use the new action.
Most Forth systems provide a warning if a word is re-defined.
: myword ; : myword ." this one prints" ; MYWORD isn't unique
The message "isn't unique" is not an error message -- it’s just a reminder to the user that a name is being used again. If this was done unintentionally, it can be undone in many Forth systems with FORGET (usage: FORGET
A new word can reference an older version in its definition.
: print-one 1 . ; : print-one ." Here is one: " print-one ; PRINT-ONE isn't unique print-one Here is one: 1
Forth does have a mechanism for recursion, but self-reference is not it. The current word is deliberately excluded from the dictionary search. In the example above, the new print-one uses the earlier version in its definition.
c. Patching
As noted already, redefining a word does not change the existing action for words already compiled. It is sometimes necessary to change the behavior of a word in such a way that any words already compiled use the new action. This can be done in at least two ways.
1. Vectored Execution
If it is known that a word may need to have its action changed, there is a mechanism for "deferred execution". The method defines a word that executes a stored address (vector). Changing the stored address changes the behavior of the word.
I used this feature in the permutation package to permit a switch, after the fact, between left-to-right and right-to-left multiplication:
DEFER Direction : Left->Right ['] NOOP IS Direction ; : Right->Left ['] SWAP IS Direction ;
The behavior of the word Direction is switched between a NOOP (no operation) and SWAP. This switchable word is used at the start of the code for P*.
Vectored execution is also used in the "print to file" code. Win32Forth, like many other Forth systems, uses deferred execution for basic output words EMIT, TYPE, and CR. We can switch the behavior of these words. During printing to a file we install versions that not only print to the console but also send output to a file.
Vectored execution can also be used effectively in development to test several versions of a word: The code is written with a vectored word, and alternatives can be installed "on the fly".
For clarity of code, it is important to document, at the point where a vectored word is created, the type of behavior that will be filled in.
2. Patching a definition
The dictionary entries themselves occupy accessible memory. One can often change the behavior of an existing word (e.g., to fix a bug) by altering an existing dictionary entry directly. Details of this process depend on the implementation of Forth and are beyond the scope of this article.
Evolution of a Computer Application - Summary
The methodology I have described in this article involves creating a special-purpose, problem-oriented language. I use a base language (Forth) that permits users to get involved in the creation of the programming language. Forth provides access to memory, the input stream(s), and the process of compilation. (Note 12) With this access one can implement almost any type of data structure or language syntax. (Note 13)
A special-purpose language provides a means of expression that is conceptually closer to the application area. In Groups32 I have used the ability to conceptualize in terms of groups, subgroups, sets, etc. Notice that, while early definitions are in terms of integers and addresses, later definitions are expressed more in terms of group elements, subgroups, etc.
I have used a "middle out" approach to the design and implementation of a software system: A rudimentary, functional, system is created first. This core system is the major tool in the development of more extensive and refined systems.
I have used this methodology to produce systems for research as well as for instruction. These systems provide an interactive computing environment. They are extensible: In research, a system can be extended and modified to meet the needs that arise as a project progresses; in instruction, a system can be tailored to the needs of a particular class.
Evolution of a Computer Application - Resources
-
The Forth implementation used in this work is Win32Forth, written by Tom Zimmer and Andrew McKewan. It is in the public domain. A complete version of Win32Forth and supplementary materials can be found on the Forth Interest Group Web site.
- A variety of non-commercial Forth implementations and other Forth resources can be found on the same site. There are also links at this site to the web pages of vendors of commercial Forth systems.
- More Forth resources are listed on my Web site.
- You can download a ZIP file containing executables (binaries) for the two versions of the groups system discussed in this article. In most cases the ZIP file can be downloaded just by clicking here.
- In some cases it might be necessary to obtain the ZIP file using anonymous FTP. Here is the procedure:
- Connect to ftp math.ucsd.edu
- Use "anonymous" as the username
- Use your email address as password
- cd pub/jwavrik
- type "binary" to ensure a binary transfer
- type "get wavrik_executables.zip"
The following papers give background information on the approach to system development used in this paper, as well as source code for some of the features.
- J. J. Wavrik, "User-defined systems for pure mathematics," Proc. FORML Conference, (1989), 97-103. view/download (pdf)
- J. J. Wavrik, "Handling multiple data types in Forth," Journal of Forth Application and Research, v. 6, no. 1 (1990), 65-76. view/download (pdf)
- J. J. Wavrik, "An Extensible User Interface", Forth Dimensions XIX, no. 6 (1998), 19-27. view/download (pdf)