This section contains the targets of hyperlinks in the article.
Forth was invented (or perhaps discovered) during the 1970s by Charles Moore. Its original use was for applications involving hardware control and instrumentation. It was used as a high-level, portable replacement for assembly language programming. The language was designed for simplicity, flexibility, and speed. It is currently used to assist in the design and testing of experimental hardware control applications.
A major use of Forth is to program "embedded systems", i.e., computers that are included in other products.
In many respects the advantages of Forth for developing experimental hardware control systems are similar to the advantages we exploit for work in mathematics. It provides a simple comprehensible foundation to which a variety of features can be added. It is a language suited for building language features.
Here are some of the attributes that make Forth a good choice for this work:
![]()
IF and THEN
This level of detail is beyond the scope of my intended simple introduction.
However, you may be curious about exactly how one can define words that do what
we have asserted that IF and THEN do.
Here are the simplest forms of the definitions of IF and THEN used in traditional
Forth implementations:
: IF COMPILE ?BRANCH HERE 0 , ; IMMEDIATE: THEN HERE SWAP ! ; IMMEDIATE
: IF |
Start definition of IF |
COMPILE ?BRANCH |
Compile conditional branch instruction |
HERE |
Put current address of dictionary pointer on stack |
0 , |
Compile a zero as a placeholder to be filled in by proper address. |
; |
End the definition |
IMMEDIATE |
Tag this as an immediate word |
| |
|
: THEN |
Start definition of THEN. Remember that IF left an address on the stack. |
HERE |
We put where we are now on the stack |
SWAP |
Put location of missing address on top of current address |
! |
Store current address. |
; |
End the definition |
IMMEDIATE |
Tag this as an immediate word |
In most Forth implementations additional information is put on the stack to check that conditionals are properly paired (an IF with a THEN, etc.)
![]()
Here, at the very lowest level, is what proved to be a very useful capability of the system and of the ability to program it. A modified version of the TABLE word has been used, for example, to export the group tables (together with additional information) in a form suited for use by a Java Applet (see Groups15).
We have mentioned the use of Groups32 to print information for input into spreadsheets for sorting an analysis. This was used by Evelyn Manalo (see Honors Theses) to develop a Maple procedure for printing the cycle decomposition of an abelian group and for work on the isomorphism problem for groups of order 1-32 (i.e. to find an efficient way to classify groups of order 1-32).
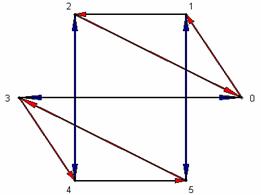 Recently
Groups32 was used to generate data suitable for use in Maple for a student
research project on Cayley graphs (see Honors Theses).
The student, Sonja Willis, wanted to use the Maple networks package to print
Cayley graphs with colored arrows rather than the green lines that the package
normally produces. To do this one needs group data with the edges produced
by the various generators kept separate. Some programming in Maple was needed
to produce the colored arrows. The data were produced using Groups32. The
figure at the right shows an example for group #8 (which is S3). The information
transported was produced by a word PrintMaple (see below).
Recently
Groups32 was used to generate data suitable for use in Maple for a student
research project on Cayley graphs (see Honors Theses).
The student, Sonja Willis, wanted to use the Maple networks package to print
Cayley graphs with colored arrows rather than the green lines that the package
normally produces. To do this one needs group data with the edges produced
by the various generators kept separate. Some programming in Maple was needed
to produce the colored arrows. The data were produced using Groups32. The
figure at the right shows an example for group #8 (which is S3). The information
transported was produced by a word PrintMaple (see below).
8 Subgroups * = Normal subgroup Generators Subgroup 0 { } *{ A } 1 { D } { A D } 2 { E } { A E } 3 { F } { A F } 4 { B } *{ A B C } 5 { B D } *{ A B C D E F }
In this version the generators were taken from the Subgroups command. B(1) and D(3) are generators. The Maple command generated by PrintMaple is a list consisting of the set of vertices, the number of generators, and a list of sets of edges.
8 PrintMaple
Cay[8] := [{$0..5},2,[\ {[0,1],[1,2],[2,0],[3,4],[4,5],[5,3]\ }\ ,{[0,3],[1,5],[2,4],[3,0],[4,2],[5,1]\ }\ ]] :
The key to understanding what is happening here is to realize that we have created a Forth word called PrintMaple that takes a group number as input and whose action is to print a Maple command. Here are the details.
: Out$ ( addr cnt -- ) 0 ?DO DUP C@ DUP ASCII # = IF DROP SWAP 0 .R ELSE EMIT THEN 1+ LOOP DROP ; |
Making output strings with inserted numbers.
Here is a version taking the address and count of a string as input. When a # occurs in the string, it prints the number on top of the stack. |
: ?\ GETXY DROP 40 > IF ." \" CR 8 SPACES THEN ; |
This prints a Maple continuation character and line break if the line gets too long. |
VARIABLE PMFirst VARIABLE GenFirst |
These variables are used to determine whether an item is the first one being printed. |
: PrintMaple ( grp -- ) >Group CR
Gord 1- Gnum
s" Cay[#] := [{$0..#},"
Out$ PMFirst ON |
This prints the function header and set of vertices. The first # is the number of the group and the second is Gord-1 |
Gnum 144 <
IF Gnum Generate-Subgroups
#Subgroups 1- Generators \ gens
ELSE 2198 \ {bcehl}
THEN |
Generators are obtained from the Subgroups command. The last subgroup generated is G itself. Groups32 does not compute subgroups for group number 144 – so this is treated as a special case. |
DUP #Set S" #,[\" Out$ CR 8 SPACES |
Print number of generators |
GenFirst ON
32 0 DO I OVER MEMBER?
IF \ Output for a generator
GenFirst @
IF ." {" GenFirst OFF
ELSE ." ,{" THEN |
Test if loop index is a generator.
We will print a set bracket { only before the first set of edges, otherwise we print ,{ |
PMFirst ON For-All-Elements DO PMFirst @ IF ." [" PMFirst OFF ELSE ." ,[" THEN |
For each generator we print the corresponding edges [a,ag]. We print a comma between edges. |
I J G* I S" #,#]" Out$ ?\ LOOP ." }\" CR 8 SPACES |
We print the pair for an edge and a continuation
character if necessary. Then close the set of edges with } Finally, end the structure. |
![]()
The permutation package can be used to produce a group table for any abelian
group. The Fundamental Theorem of Abelian Groups says that any finite abelian
group is a product of cyclic groups. The permutation package allows us to
create products of cyclic groups by entering disjoint cyclic permutations
for generators. Thus ![]() can
be realized as the subgroup of S6 generated by ( 1 2 3 4 ) and
by (5 6). This group is produced in the permutation package by:
can
be realized as the subgroup of S6 generated by ( 1 2 3 4 ) and
by (5 6). This group is produced in the permutation package by:
6 Size! Gen: ( 1 2 3 4 ) Gen: ( 5 6 ) Make-Group Show-Table 1 2 3 4 5 6 7 8 2 1 4 3 6 5 8 7 3 4 5 6 7 8 1 2 4 3 6 5 8 7 2 1 5 6 7 8 1 2 3 4 6 5 8 7 2 1 4 3 7 8 1 2 3 4 5 6 8 7 2 1 4 3 6 5
To generate the tables for abelian groups of orders 17-31, we automated this idea. The tables were actually generated using an earlier version of the permutation package that used a slightly different representation for the permutations and that directly stored the groups in the internal representation. Here is a more modern adaptation that introduces an interesting useful possibility: Generate a script file, and then run the script file to produce the desired results.
A script file is a file of commands. It could be a file of Forth/Groups32 commands (as in this case). It could also be a file of commands for some other system -- we often produce script files for Maple. The easiest way to make a script file is to capture output to the screen in a file. I wrote for Groups32 a "print to file" utility for this purpose. A script file is loaded into Forth by INCLUDE <filename>. The Forth system then reads and executes commands from this file as if they were being typed at the keyboard.
First we need a Groups32 command called CycDecomp. The stack diagram is ( s1 s2 … sk n -- ), where s1, s2, … , are the sizes of the component cycles, and n is the sum of the sizes. (It will determine the Sn in which they are considered to be permutations.) The output of CycDecomp will be the commands needed by the permutation package to produce the table of the associated group.
2 3 5 CycDecomp 5 Size! Gen: ( 1 2 3 ) Gen: ( 4 5 ) Make-Group Show-Table
Notice that the word CycDecomp does not execute these commands -- it just prints them on the screen. If the print-to-file feature is active, these commands are also captured to a file.
Win32Forth can also print the console window to a file -- so, for a limited amount of output, it may be sufficient to use this feature.
The abelian groups of order n correspond to partitions of n. Thus, for example, we can partition 6 = 3 + 2 + 1. If we use
1 2 3 6 CycDecomp
we obtain commands
6 Size! Gen: ( 1 2 3 ) Gen: ( 4 5 ) Gen: ( 6 ) Make-Group Show-Table
Executing these commands produces the table
1 2 3 4 5 6 2 1 4 3 6 5 3 4 5 6 1 2 4 3 6 5 2 1 5 6 1 2 3 4 6 5 2 1 4 3
By inspection, this table represents an abelian group of order 6. "1"
is the identity. Element "4" has order 6 -- so this is the table
of ![]() We must,
therefore, select from all partitions of n those that produce non-isomorphic
groups. Here are the commands for groups of orders 17-22:
We must,
therefore, select from all partitions of n those that produce non-isomorphic
groups. Here are the commands for groups of orders 17-22:
17 17 CycDecomp 2 3 3 8 CycDecomp 2 9 11 CycDecomp 19 19 CycDecomp 2 2 5 9 CycDecomp 4 5 9 CycDecomp 3 7 10 CycDecomp 2 11 13 CycDecomp 23 23 CycDecomp 2 2 2 3 9 CycDecomp |
2 4 3 9 CycDecomp 8 3 11 CycDecomp 5 5 10 CycDecomp 25 25 CycDecomp 2 13 15 CycDecomp 3 3 3 9 CycDecomp 3 9 12 CycDecomp 27 27 CycDecomp 2 2 7 11 CycDecomp 4 7 11 CycDecomp |
29 29 CycDecomp 2 3 5 10 CycDecomp 31 31 CycDecomp 2 2 2 2 2 10 CycDecomp 2 2 2 4 10 CycDecomp 2 4 4 10 CycDecomp 2 2 8 12 CycDecomp 4 8 12 CycDecomp 2 16 18 CycDecomp 32 32 CycDecomp |
The definition of Show-Table was changed, for the purpose, to print the tables in the format used to load tables from text files. Here is the format:
9 7 ->Group 0 7 >ROW 0 1 2 3 4 5 6 1 7 >ROW 1 2 3 4 5 6 0 2 7 >ROW 2 3 4 5 6 0 1 3 7 >ROW 3 4 5 6 0 1 2 4 7 >ROW 4 5 6 0 1 2 3 5 7 >ROW 5 6 0 1 2 3 4 6 7 >ROW 6 0 1 2 3 4 5
Here is the procedure:
![]()
Here are the three definitions for G* that were used in the timing chart:
: 'ELE ( ele1 ele2 - addr ) \ compute address of product ID - SWAP ID - GORD * + \ offset from base address GBLK BLOCK GOFFS + \ address of start of table + ; \ address of element : G* ( ele1 ele2 - ele1*ele2 ) 'ELE C@ ;
: G* ( ele1 ele2 - product ) MaxOrd * + \ compute offset of product Grp @ + \ add the base of the table C@ ;
CODE G* ( i j -- i*j ) \ ASSUME MaxOrd=32 SHL EBX, 5 \ Multiply j by 32 POP EAX ADD EBX, EAX \ Add i MOV EAX, Grp [EDI] \ Add group offset ADD EBX, EAX SUB EAX, EAX \ byte at this address MOV AL, [EBX] [EDI] MOV EBX, EAX NEXT END-CODE
There are 9 words in Groups32 that are coded in assembly language.
![]()
Most Forth words take parameters from the stack and return results to the stack. The Forth word WORD reads the input stream. The object is to convert the text following it into an internal form (a counted string).
A counted string is stored in memory as a count (one byte) followed by the ASCII codes of its characters. The string ABC would be stored as
| 3 | 65 | 66 | 67 |
Once it is stored, the address of the count byte is passed to other words on the stack. We imagine that a string is on the stack. We say to ourselves "a string is on the stack". We tell our friends "a string is on the stack". In reality, the stack contains just the address of the count byte, but we can conceptualize as if the stack contained the string itself. This is typical of the way that we make our system appear to handle sophisticated types of data on the stack.
Once it is stored the address of the count byte is passed to other words on the stack. This is how we imagine a string to be on the stack.
WORD ( delim - c-addr ) is an input word. It reads the text that follows it when it acts. It stores the text as a counted string in a temporary location (in most Forth implementations, this is at the end of the dictionary), and it returns the address of the counted string. WORD is usually used in definitions that immediately do something with the string (process it or move it elsewhere).
WORD is the word the system uses when it interprets the input stream word by word. It could, but usually doesn't, use a temporary storage mechanism. Thus each incoming word is placed in the same temporary location. Forth gets away with this because the string is immediately processed. If you try to see what WORD does (as a referee of this paper did) by typing a command line, you will find it is a shy little animal: Just trying to look at it chases it away. You might try
BL WORD ABC COUNT TYPE
and you will get TYPE as the response. What happens is that BL WORD does read the ABC and make it a counted string (stored at the end of the dictionary). But then the Forth interpreter uses WORD again to read the string COUNT (and stores it at the end of the dictionary). It looks this up in the dictionary and executes it. It then reads TYPE (and stores it at the end of the dictionary) and looks it up and executes it.
The ABC string was overwritten by COUNT and then by TYPE -- all of which were put at the same address. The very act of trying to observe the result of BL WORD ABC destroys what you are trying to observe!
This is really not as horrible as it seems. The counted string produced by WORD is put in a temporary place known to be available -- so everybody uses that place. If you really want to read the input stream yourself, you can -- but you must do something with the counted string the system uses WORD to read the next command.
My suggestion, if you want to make a string package, is that you make some sort of temporary storage mechanism. I personally use the method discussed in this article. Others have used a string stack or a circular buffer. Then make an input word that uses WORD but immediately moves the string to a temporary storage location.
It is also legal to use WORD and immediately do something with it.
![]()
Early versions of Forth ran on machines using 16 bits for integers and addresses. This meant that one could address only 216 = 65536 memory locations. This 64k of address space included the code for the operating system and the language implementation, leaving very little space for the application code and data. Virtual memory is a scheme for treating the disk (it was floppy at the time) as if it were real memory: Data could be stored on disk and read to "real" memory when needed -- and unneeded data would be paged out from "real" memory to disk. The trick was to make this process of swapping between disk and real memory as transparent as possible.
Forth was developed at a time when computers were (by present standards) very small. An entire University was served by a computer with 4 Meg of RAM. A personal computer (such as my first one) was considered rather powerful with 16k of RAM. When I expanded to 64k I was asked, seriously, what I would do with all that memory.
The operating systems of the time were too small and unsophisticated to include a virtual memory system. Forth was regarded as rather advanced because it had such a scheme.
The virtual memory scheme works like this: Imagine the disk to be organized as "blocks" of 1024 bytes. We number the blocks:
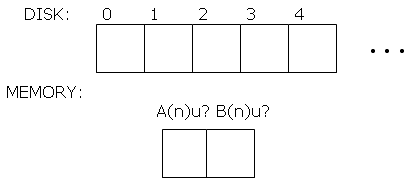
Real memory has room for only two boxes that can store data read from disk. There are two vital pieces of information stored about these two "buffers": the number of the disk block currently in memory, and a flag (true or false) to indicate whether this information has been "updated" or changed.
If you want to use an item stored in a disk block, it must be read into one of the buffers. It can then be read and changed just as if it is in memory. If it has been changed, it should be saved to disk before the buffer is reused. All this is done by the word BLOCK.
BLOCK ( n - addr )IFblock n is already in a buffer, return its address
ELSEget the least recently used buffer
if it is marked "update", write its contents to disk
read the data from disk block n to this buffer
mark the buffer as not updated
return the address of the start of the buffer
As you can see from this, if a certain disk block contains the data for one or more groups, these data are read into a buffer -- but then all computations on that group can be performed using the data in memory. It is almost as if the group data were in memory all the time. We just make all computations refer to the address (returned to us) of the start of the buffer that holds the data.
So we have stored each group table in a certain disk block (the number is GBLK). The start of the table is a certain distance or offset from the start of the block (GOFFS). The rows of the table are stored one after another, so we need to know the group order (GORD) to find a particular product. We will also need to know the number of the current group (GNUM). This vital information about all of the groups was stored in block 0.
So the scenario is this: You want to study group n. You go to block 0 (IDXBLK) where the triples GORD, GBLK, GOFFS are stored. Each of these (in the original 16-bit version) occupies 2 bytes. To find the triple for group n, you must add 6n to the address of the start of the block. So, if Base denotes the address of the start of block 0, then
GORD is at address Base + 6n,
GBLK is at address Base + 6n + 2,
GOFFS is at address Base + 6n + 4.
To get the address of the base of the group table we do GBLK BLOCK GOFFS +. GBLK BLOCK will load the disk block containing the table into memory and return the base address of the block. Adding GOFFS will give the address of the start of the table.
Once the triple GORD, GBLK, GOFFS is read from block 0, we no longer need to have block 0 in memory. When we do group computations in the current group, the data for that group are written from disk to memory and stay in position. No further disk access is necessary to compute in this group.
: >GROUP ( n -- ) \ set GORD GBLK and GOFFS ( n ) DUP TO GNUM \ save group number ( n ) 6 * ( 6n ) IDXBLK BLOCK + \ address of triple ( addr ) DUP @ TO GORD ( addr ) 2+ DUP @ TO GBLK ( addr+2 ) 2+ @ TO GOFFS ;
The original data files used 16-bit integers, so the three elements of the triplet occupied 2 bytes each. When an original data file is used with a 32-bit version of Forth, the fetch operation @ must be replaced by W@ so that it gets a 16-bit rather than a 32-bit value.
![]()
In Groups16 the table for a group of order m was stored as m x m consecutive bytes to save memory. In Group32 all tables are stored as 32 x 32, regardless of the group order, to increase speed.
The group table for ![]() ,
of order 4, looks like this in two dimensions:
,
of order 4, looks like this in two dimensions:
| A |
B |
C |
D |
| B |
C |
D |
A |
| C |
D |
A |
B |
| D |
A |
B |
C |
In memory this is stored by rows:
ABCDBCDACDABDABC
If we number the rows and columns 0, 1, 2, 3, then the entry in row r and column c occurs 4r + c slots from the start of the table. Thus the first row (r = 0) is at offsets 0, 1, 2, 3 from the start of the table. The next row is at 4, 5, 6, 7.
The word 'ELE ( ele1 ele2 - addr ) calculates the address of the product of ele1 and ele2. Remember that in Groups16 the elements are represented as ASCII characters -- so we must subtract ID (the code for "A") to get r and c.
: 'ELE ( ele1 ele2 - addr ) ID - ( ele1 c ) SWAP ID - ( c r ) GORD * + ( r*ord+c ) GBLK BLOCK \ address of block for table GOFFS + \ add the offset to get \ base address of table + ; \ get address of element: 'ELE ( ele1 ele2 - addr ) Compute row and column numbers compute displacement of element (r*ord+c) get base address of stored table get address of element ;
![]()
Here is a more detailed discussion of the code.
: EORDER ( x - order ) We plan to take the original element and create its powers xn in a loop.
We will quit when we get a power that is the identity element.ID We put the identity on the stack as x^0. So the stack has (x x^0).GLIMITS DO ( x x^n ) The loop is taken over all elements of the group. I should actually have made
this GORD 0 DO -- it would then have been clearer that we are looping over powers. I just didn't think of it at the time. The ( x x^n ) above is a comment. It is helpful to know that each time we are at the start of the loop this is what is in the stack.OVER If we had ( x x^n ) in the stack, we now have ( x x^n x ) .G* Now we have (x x^[n+1] ) .DUP ID = Test if it is the identity, but DUP it first so that it is not removed from the stack .IF 2DROP This removes the x and x^[n+1] .I ID - 1+ Due to the way the loop limits were set up, this gives the exponent.LEAVE This causes an exit from the loop.THEN Notice that if we did not exit from the loop we now have ( x x^[n+1] ) in the stack, and the loop repeats with the stack as indicated by the stack diagram after DO.LOOP ;
![]()
CREATE SQ 20 ALLOT : #SQUARES ( grp# -- n ) >GROUP SQ 20 ERASE GLIMITS DO I I G* ID - SQ + 1 SWAP C! LOOP 0 20 0 DO SQ I + C@ + LOOP ;
This code is short, but might benefit by some analysis. The point here is to run through the group computing the squares of the elements. Each time a square is computed, a record is made that this element is a square. The structure is this:
: #Squares ( grp# -- n ) >Group Initialize-SQ Mark-Squares Count-Marks ;
An array-like structure, SQ, is used to record the marks. There is no standard ARRAY word in Forth, but one can easily be defined (and a few are in the current Groups32). Rather than use general purpose machinery, we have used a more direct approach:
SQ will be the name for a block of 20 bytes. When the name SQ is used it will return the address of the start of this block. So this word sets all these locations to 0:
: Initialize-SQ SQ 20 ERASE ;
Now these memory locations are intended to be associated with group elements. Since (in the 1990 version) we represented group elements by the ASCII codes for A, B, C, …. , we must subtract ID to find the offset of a given element. x ID - SQ + will give the address in the SQ list corresponding to x. 1 <addr> C! stores the byte 1 at the given address. So now we can understand the code for marking the squares:
: Mark-Squares GLIMITS DO I I G* \ compute the square ID - SQ + \ find address of the entry 1 SWAP C! \ store 1 in this location LOOP ;
After running this code, the SQ array will have a 1 in any place that corresponds to a square and a 0 otherwise. We therefore need only to run through the array and tally the number of 1's.
: Count-Marks ( -- cnt ) 0 20 0 DO ( total ) SQ I + C@ \ gets the 1 or 0 + \ add it to the total LOOP ;
![]()