Three Hundred Years of Helping Others: Maria Gaetana Agnesi on the Product Rule – A Mini-Primary Source Project for Calculus 1 Students
If the quantity proposed to be differentiated is the product of several variables, such as \(xy\), whereas \(x\) becomes \(x+dx\), \(y\) becomes \(y+dy\), and \(xy\) becomes \(xy+ydx+xdy+dx\, dy,\) which is the product of \(x+dx\) with \(y+dy\); from this product, then, subtracting the proposed quantity \(xy\), there remains \(ydx+xdy+dx\ dy,\) but \(dx\ dy\) is an infinitely smaller quantity than each of the other two, which are the rectangle of a finite quantity with an infinitesimal, and \(dx \, dy\) is the rectangle of two infinitesimals, and therefore infinitely smaller, so this rectangle can frankly be neglected, therefore the differential of \(xy\) will be \(xdy+ydx\). [Agnesi 1748, p. 458].1
By the mid-eighteenth century, many of the ideas of what we today call calculus existed in some form, but the subject was still in its early stages of development. The state of the literature in particular attested to this: related results based on different underlying ideas were scattered throughout countless publications in different languages and printed in different countries. Luckily for the students of that era, a herculean, benevolent effort was underway. The expository genius Maria Gaetana Agnesi (1718–1799) was hard at work on her two-volume book Instituzioni Analitiche ad Uso della Gioventú Italiana (Foundations of Analysis for Use of the Italian Youth) with the aim of making accessible to the many knowledge that had previously been held only by the few.2 Not only did Agnesi’s book offer a complete introductory treatment of precalculus, differential calculus, and integral calculus in a single work, it was also one of the first calculus textbooks written in a vernacular language instead of Latin. The mini-Primary Source Project (mini-PSP) Three Hundred Years of Helping Others: Maria Gaetana Agnesi on the Product Rule enables today’s students and teachers to benefit from this marvelous work, just as those of the eighteenth century did.
|
|
|
Specifically, this mini-PSP visits the standard single-variable calculus topic of differentiation rules. While students often become adept at applying these rules through drilling, it is rare that today's standard framework of defining the derivative via a limit of a difference quotient provides them with much intuition with regards to these rules. At its worst, the somewhat mysterious difference quotient approach can lead to errors of the “derivative of the product is the product of the derivatives” variety. Agnesi’s treatment of the product rule offers an alternative framework for justifying the correct rule that may have a better chance of sticking with a first-semester calculus student. In particular, the differential explanation that she gave in the above quotation lends itself to a more visual—and thus for many of our students, more intuitive—justification of the product rule.
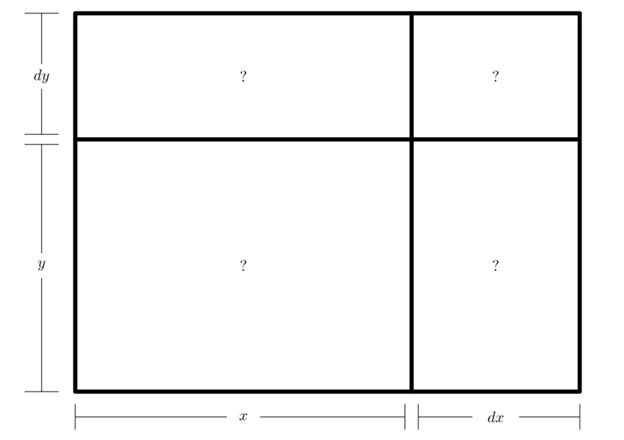
Through the project tasks, students interpret Agnesi's words as quoted at the top of this page using the labeled geometric diagram shown above, thus deriving the basic product rule. As Agnesi proceeded to extend her approach to products of three quantities [Agnesi 1748, p. 459], the mini-PSP does the same by inviting students to deduce the product rule for three factors (again with an accompanying diagram) and to then extrapolate that result to products involving four or more factors. The project ends by guiding students to follow Agnesi’s footsteps even further by deducing the power rule from the product rule. This not only establishes two of the most fundamental rules of differential calculus, but also provides the student with a very gentle introduction to inductive arguments, aiding their future studies.
The complete project Three Hundred Years of Helping Others: Maria Gaetana Agnesi on the Product Rule (pdf) is ready for student use, and the LaTeX source is available from the author by request. Instructor notes are provided to explain the purpose of the project and guide the instructor through implementation of the project.
This project is the thirtieth in A Series of Mini-projects from TRIUMPHS: TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources appearing in Convergence, for use in courses ranging from first-year calculus to analysis, number theory to topology, and more. Links to other mini-PSPs in the series, including 15 additional projects for use in introductory calculus courses, appear below. The full TRIUMPHS collection also offers one additional mini-PSP and six more extensive “full-length” PSPs for use in teaching calculus, as well as several projects based on Agnesi’s Instituzioni for use in teaching precalculus.
Acknowledgments
The development of the student projects presented in this article has been partially supported by the TRansforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) project with funding from the National Science Foundation’s Improving Undergraduate STEM Education Program under Grants No. 1523494, 1523561, 1523747, 1523753, 1523898, 1524065, and 1524098. Any opinions, findings, and conclusions or recommendations expressed in this project are those of the author and do not necessarily reflect the views of the National Science Foundation.
References
Agnesi, Maria Gaetana. 1748. Instituzioni Analitiche ad Uso della Giovent Itúaliana. Vol. 2. Regia-ducal corte, Milan.
Mazzotti, Massimo. 2008. Agnesi, Maria Gaetena. In New Dictionary of Scientific Biography, edited by Noretta Koertge, i:19–21. Farmington Hills, MI: Thomson Gale.
Mazzotti, Massimo. 2007. The World of Maria Gaetana Agnesi, Mathematician of God. Baltimore: John Hopkins University Press.
[1] The translation of this excerpt from [Agnesi 1748] was prepared by the author.
[2] From an early age, Agnesi was quite famous in Europe for the clarity and beauty of her exposition. One anecdote involved two French nobles from Burgundy who traveled to Milan in the hopes of finding works of art from classical antiquity or the High Renaissance, Raphael in particular. When they arrived in Milan, they were disappointed to have found little of what they came for, but thrilled to have stumbled upon Maria Agnesi. When they ended up at a social gathering hosted by her father Pietro Agnesi (ca 1692–1752), she spoke on the nature of tides and the origin of spring water, two complicated and controversial topics at the time. The Burgundians were blown away, saying that “She spoke like an angel about these matters” [Mazzotti 2007, p. 5]. For more details on her life, see [Mazzotti 2008].

