The accomplishments of ancient Chinese mathematicians have increasingly come to light since [Needham 1954] started to bring them to the attention of Western historians, with [Dauben 2007] providing an account of the culture’s global context that is especially useful for students and instructors. It can be argued that the utilitarian mathematics of ancient China exceeded that of the West, both in scope and quality, up to the time of the European Renaissance. The Chinese could extract square and cube roots of numbers to several decimal places, and by 500 CE they had obtained a value for \(\pi\) of \(3.14159267\), a degree of precision unknown elsewhere until after the 16th century.

Fundamental to this high level of achievement was the facility of the Chinese system of numbers and notation. From the 8th century BCE forward, they employed a decimal number system that utilized place value ordering. The numerals were written as vertical and horizontal strokes that depicted a configuration of bamboo rods, or suanzi, organized into two distinct but related sets of figures.

Figure 2. The two sets of rod numerals. Figure drawn by the author.

The first set (Figure 2a), called zeng by the Chinese, was used to denote even powers of ten: units, hundreds, ten thousands. . . . The second set (Figure 2b), hang, represented odd powers of ten: tens, thousands, hundred thousands. . . . While computing rods were initially made of bamboo, later rods were made of bone, ivory, or even jade. As conceived, the rod numerals possessed certain properties:

1. Rod numerals 1–5 are obviously simple tally symbols or stroke marks, by which a 1:1 correspondence is established between the objects being counted and the recording strokes. The symbols change to a coded symbol after a count of 5. Coded symbols are comprised of a horizontal stroke representing 5 combined with simple vertical tally strokes. A close association with hand counting is evident.
2. The symbols used to represent powers of ten are single strokes—either horizontal or vertical. Rod numeration is clearly decimal in nature and employs a positional ordering based on powers of ten.
3. The positional ordering in rod numeration follows modern conventions. Chinese mathematicians used decimal-based, place-value systems of recording numbers well before the Common Era.

In situations involving numerical problem-solving, computations were performed on a flat surface: the floor, a tabletop, or even a separate board, using a set of bamboo rods (approximately 13 cm long). Rod configurations representing numerical quantities were laid out horizontally from the right to the left in ascending powers of ten, in contrast to traditional Chinese textual writing, which proceeded vertically from the top of a page to the bottom. In the computational process, vertical columns were used to ensure place value, and mathematical operations proceeded downward within columns. Thus, the computing surface was partitioned into a grid in which each cell could, or did, contain a rod configuration. As shown in Figure 3, some existing woodcut prints depict computing situations. When the results of computations were written out, the rod configurations were copied, giving rise to the set of rod numerals.

Figure 3. A mathematician performs rod calculations before his master.
Japanese wood cut print by Seijutsu Sangaku Zue, 1795. Wikimedia Commons.

This system of computation and number recording was greatly admired throughout East Asia. Mathematicians in both Korea and Japan adopted the use of computing rods, sangi, and their numerical interpretation. Rod numerals can be read in a manner similar to our modern numerals.

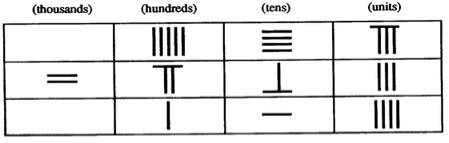
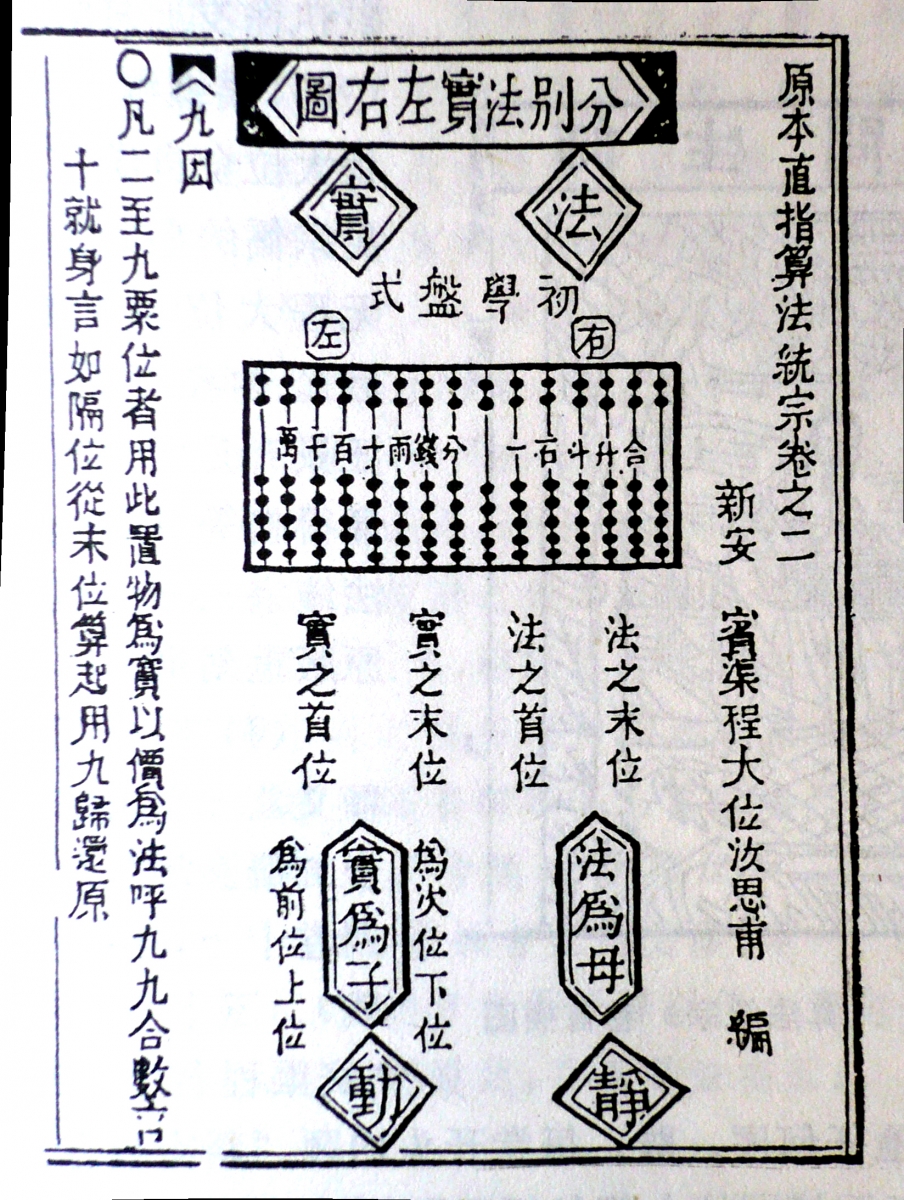
Figure 4. Place value chart for rod numerals. Figure drawn by the author.
The rod positions in the top row represent the number \(548\), in the second row \(2763\), and in the bottom row \(114\).

Thus, these numerals evolved directly from a system of concrete counting and computing. For today’s students, too, they supply a semi-concrete image of mathematical relationships and, as such, provide working models for numbers. Numerical relationships are intrinsically embedded in the numerals themselves and encourage mathematical understanding, an attractive pedagogical feature.

Rod numeral algorithms for the basic arithmetical operations parallel those we employ today [Lam and Ang 2004]. The visual pattern presented by the rod numerals facilitates the performance of simple arithmetic operations. For example, consider how the addition of \(7 + 8\) was accomplished, as is illustrated in the diagram below. A trained computer would first note the strokes for the numeral \(5\), i.e., the horizontal strokes, ① combine them and carry one horizontal stroke into the next column. The remaining vertical strokes would then be added together ②. In performing this procedure, a rod was physically “carried” to the next column—the ancient Chinese used this term to describe the process of moving ahead one tens place on the left in their numeration scheme.

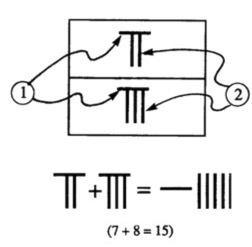
Figure 5. An example of the addition operation. Figure drawn by the author.

In the subtraction process, the Chinese used the term “borrow” to indicate the moving of a ten to the right to permit a subtraction. Thus, in principle, their algorithms for performing addition and subtraction were very similar to ours. Where subtraction eliminated a tens position, the rod protocol left an appropriate blank space in the corresponding cell on the computing surface. For example, \(107\) would be represented with rods on a board as:

Figure 6a. Evolving techniques for representing zero place value. Figure drawn by the author.

and then transcribed in the following manner:

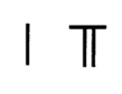
Figure 6b. Evolving techniques for representing zero place value. Figure drawn by the author.

Knowledgeable mathematical scribes would be able to discern the number of empty position places in a numeral and interpret the designated number correctly. A written symbol, 0, was adopted as an empty placeholder for use by the Chinese in the 12th century CE. Thus, from that time onward, \(107\) would be recorded as:

Figure 6c. Evolving techniques for representing zero place value. Figure drawn by the author.

In the event that a numerical quantity became negative during the computational process, a supplementary rod was laid diagonally across the existing configuration. Another amazing fact concerning rod numerals is that from the 2nd century BCE onward they came in two colors, black and red, to represent negative and positive numbers respectively! What is the significance of these two colors in referring to a mathematical situation today? For tactile discrimination, positive rods had a triangular cross section and negative rods a square cross section. An examination of old Chinese arithmetic manuals reveals rules for working with negative numbers that are the same as those we use today. One such extant reference is Sun Zi suanjing, from ca 400 CE [Lam and Ang 2004]. The foundations for rod multiplication and division are based on the concepts of repeated addition and subtraction, respectively. Chinese multiplication and division algorithms also mirrored our own, depending on the use of partial sums and partial products. Rod procedures for these operations are rather too complex for consideration here; however, they are fully examined and discussed in sources such as [Straffin 1998] and [Swetz 1979].

Rod configurations allowed for the expression of both common and decimal fractions. Common fractions were expressed by two rod configurations: a numerator, referred to in Chinese as the “son,” and a denominator, the “mother”. A relationship of dependence was implied between the two mathematical entities. So, mother and son would comprise a fraction, one placed vertically above the other; for example, \(3/8\) would be represented as shown below.

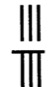
Figure 7. A fraction in rod numerals. Figure drawn by the author.

This convention was adopted by Islamic merchants, brought back to their home countries, and utilized in commercial and business computations. Eventually, their computer-scribes placed a line between the two numerical indicators. This later version, the one we know today, was transmitted to Europe in 1202 by the Italian merchant, Leonardo of Pisa [Sigler 2002]. For the Chinese, decimal fractions were indicated within rod placement by their position on the computing surface. Numerical entries positioned in the cells to the right of the units position represented descending powers of a tenth.

The oldest extant Chinese mathematical classic, the Jiuzhang Suanshu (Nine Chapters on the Mathematical Art) of ca 200 BCE, provides evidence of varied, and more advanced, Chinese mathematical activity [Schwartz 2018]. For example, the division process using rods was modified and developed into a strategy for extracting square and cube root of numerical quantities. Before the first year of the Christian calendar, Chinese mathematicians were obtaining accurate numerical roots to three decimal places. Their technique would appear much later in European mathematical history, in 1819, described as “Horner’s Rule” and named after the British mathematician William George Horner (1786–1837).

The contents of the Jiuzhang also indicate that Chinese users were familiar with the binomial expansion as well as posing and solving quadratic and cubic equations. A systematic means for determining the numerical coefficients of the binomial expansion was devised by mathematician Jia Xian around 1100 CE. Jia depicted the coefficients in a triangular array. Later, the noted mathematician Yang Hui (fl. 1238–1298) expanded Jia’s work and published his findings in an enlarged triangular figure. Within this diagram, Yang expressed his numbers using rod numerals. Six hundred years hence, this numerical triangle would become known as “Pascal’s Triangle,” honoring the French mathematician Blaise Pascal (1623–1662).

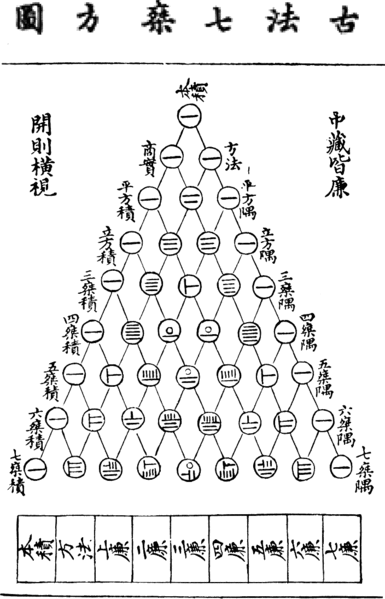
Figure 8. Wood cut print of Yang’s triangle as published in 1303 by the mathematician Zhu Shije in his Si Yuan Yu Jian. Can you read the numbers? (Some are variant versions.) Is there a mistake? Wikimedia Commons.

The peak of Chinese algebraic accomplishment using computing rods and a board was achieved in the 14th century by the mathematician Zhu Shijie (c. 1260–c. 1320). Zhu developed a method to solve equations containing up to four unknowns. His “Four Element Method,” as discussed in his Si-yüan yü-jian (Jade Mirror of the Four Unknowns) of 1303 CE, included the entities known as: Heaven, Earth, man, and matter.

Rod layouts on the computing surface also revealed visual numerical patterns that mathematicians could interpret. Rectangular arrangements were most common. In working out problems with rods, Chinese mathematicians recognized the existence and influence of unknown variables. They distinguished between them and allowed for their presence within rod configurations. Systems of linear equations could be laid out as rectangular arrays of rods. For instance, the eighth chapter of the Jiuzhang Suanshu discussed such systems. In contemporary mathematics, we would recognize such an array as a matrix [Hart 2011]. The ancient Chinese calculators treated them as such and solved them by matrix-like operations that today we would recognize as Gaussian Elimination, a process credited to the German mathematician Carl Friedrich Gauss (1777–1855) [Grcar 2011]. Chinese solution techniques also allowed for the consideration of linear systems involving indeterminant situations.

While the pedigree of achievements with rod numerals was impressive, the knowledge and understanding of the numeration system was limited to a small number of specialized scholars. By the time of the Yuan Dynasty (1206–1368), commercial considerations necessitated a computing device that was faster and more popular than computing rods, one that was less complex in its conception and more mechanical in its required working process. To meet this need, the bead abacus, or suanpan, was developed. Its basic principles were directly derived from the computing rods and board. The earliest illustration of this device can be found in the 1592 Suan fa tong zong (General Source of Computational Methods), compiled by the arithmetician Cheng Dawei (1533–1606). On the Chinese abacus, columns of seven beads are divided into two groups comprised of 2 five-counters, or Heaven beads, and 5 unit counters, or Earth beads.

Figure 9. A Ming dynasty suanpan as shown in a then-contemporary text. Wikimedia Commons.

Thus, the Chinese abacus is the terminal product of a two-thousand-year-old computing tradition that began with the fingers of the human hand as in the ideogram at the beginning of this article, moved to a set of computing rods, and finally ended with a fixed frame containing columns of vertically-movable beads. This computing device dominated Chinese mathematics calculation from the time of the early Ming Dynasty (1368–1644 CE) well into the era of Mao Zedong in the 1960s. During this period, all Chinese school children performed finger exercises to learn the ‘art of the beads’ and become proficient on the abacus. Now, these children use an electronic hand calculator.

Figure 10. A depiction of an abacus being used. The image is from a 1758 edition of the Suan fa tong zong. It is entitled “Discussions on difficult problems between master and pupil.” This illustration, in various forms, was used in earlier Chinese texts at least as early as 1592. Waseda University Library.

Now that we have some historical background on the development and use of Chinese rod numerals, how can this knowledge be used in the training of preservice elementary teachers? While they may have learned about Roman numerals in school and encountered Egyptian (hieroglyphic) or Babylonian (cuneiform) numeration systems as undergraduates, they may not have heard of rod numerals. However, Chinese rod numerals are easier to understand and simpler to work with than these other ancient numeration systems. Introducing the concept of Chinese rod numerals, even anecdotally, fosters not only awareness, but also a cross-cultural appreciation for mathematics and a broader historical mathematical orientation. Holding an examination and discussion of rod numerals in the classroom can impart several historically-relevant facts, namely:

1. The Chinese were the first people to use a decimal place value numeral system.
2. They were also the first to employ a system of decimal fractions.
3. Their arithmetic is recognized as the first in the world to accommodate negative numbers.

Instructors could also show preservice teachers how to devise activities employing rod numerals for young students. In particular, the rods lend themselves to number recognition exercises and exploration. For example, a set of rods can be made from match sticks that have a square cross section or cut from a flattened paper soda straw. (Remember the rods should not roll.) Of course, a set of rods could also be cut out of stiff paper or cardboard.

The demonstration rods then could be manipulated on a document camera (i.e., the instructor could place rod number configurations on the screen of the projector to form images for the class to identify). A video by Jeff Suzuki [2020] could assist instructors with demonstrating the basic properties without having to write their own lectures:

Students of all ages also enjoy manipulating rods to form their own numerals and challenging their friends to correctly identify the number represented. Any flat surface—such as a table or floor—can be made into a computing board. Masking tape, applied to designate decimal columns, reinforces place value and encourages renaming. Able students can build on their experience with rod numerals to further explore the arithmetic of computing rods. Instructors might ask: How do you think subtraction was performed using rods? Multiplication? Root extraction? Indeed, many questions can be asked and fruitful learning experiences constructed around the Chinese rod numerals.

​If deeper or more extended study is desired, Primary Source Project modules such as [Beery et al. 2004] and [Flagg 2017] are available for secondary school students and undergraduates.

If a bundle of sticks had such a prolonged and productive involvement with mathematics, then where do we see evidence of their existence today? The traditional written characters used to express some numbers in China and Japan bear vestiges of their heritage in counting rods. Specifically, Ei ,er, and san, the first three counting numbers, provide evidence of rod origins:

Figure 11. Characters for the numbers \(1\), \(2\), and \(3\). Figure drawn by the author.

Further, and perhaps more interesting, is the conjecture by historians of mathematics such as Wang Ling, Joseph Needham, and Lam Lay Yong and Ang Tian Se that our contemporary numeral system is derived from rod placements [Xu 2005]. They suggest that, as rod numerals were recorded and copied over centuries, scribes became complacent and hastened their writing process, gradually slipping into more cursive forms as illustrated below.

Figure 12. A conjectured evolution of numeration systems. Figure drawn by the author.

What do you think? Perhaps our numeral system could more correctly be designated as the ‘Sino–Hindu–Arabic’ numeral system. Such a title might be more encompassing and historically revealing.

References

Beery, Janet, Gary Cochell, Connie Dolezal, Angi Sauk, and Linda Shuey. 2004. Negative Numbers. In Historical Modules for the Teaching and Learning of Mathematics (CD), edited by Victor J. Katz and Karen Dee Michalowicz, 34–44. Washington, DC: Mathematical Association of America.

Dauben, Joseph W., ed. 2007. Chinese Mathematics. In The Mathematics of Egypt, Mesopotamia, China, and Islam: A Sourcebook, edited by Victor Katz, 187–384. Princeton and Oxford: Princeton University Press.

Flagg, Mary. 2017. Solving a System of Linear Equations Using Ancient Chinese Methods. Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS): Linear Algebra. https://digitalcommons.ursinus.edu/triumphs_linear/1.

Grcar, Joseph F. 2011, June/July. Mathematicians of Gaussian Elimination. Notices of the AMS 58(6): 782–792.

Hart, Roger. 2011. Chinese Roots of Linear Algebra. Baltimore: Johns Hopkins University Press.

Lam Lay-Yong and Ang Tian Se. 2004. Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China. Rev. ed. Singapore: Scientific Press.

Needham, Joseph et al. 1954–present. Science and Civilization in China. 7 vol. Cambridge: Cambridge University Press.

Schwartz, Randy K. 2018, December. A Classic from China: The Nine Chapters. Convergence. DOI:10.4169/convergence20181231.

Sigler, Laurence E., trans. 2002. Fibonacci’s Liber Abaci. Berlin: Springer-Verlag.

Siu Man-Keung. 2000. An Excursion in Ancient Chinese Mathematics. In Using History to Teach Mathematics: An International Perspective, edited by Victor Katz, 159–166. Washington, DC: Mathematical Association of America.

Straffin, Jr., Philip D. 1998, June. Liu Hui and the First Golden Age of Chinese Mathematics. Mathematics Magazine 71(3): 163–181.

Suzuki, Jeff. 2020. Chinese Rod Numerals. https://www.youtube.com/watch?v=RnZhwHESI2U.

Swetz, Frank J. 1979, January. The Evolution of Mathematics in Ancient China. Mathematics Magazine 52(1): 10–19. DOI: 10.1080/0025570X.1979.11976742.

Swetz, Frank J. 1987. Capitalism and Arithmetic: The New Math of the 15th Century. Chicago: Open Court Publishing.

Volkov, Alexei. 2018. Chinese Counting Rods: Their History, Arithmetic Operations, and Didactic Repercussions. In Computations and Computing Devices in Mathematics Education Before the Advent of Electronic Calculators, edited by Alexei Volkov and Viktor Freiman, 137–188. Springer Nature Switzerland.

Xu Yibao. 2005, September 10. Review of Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China, by Lam Lay-Yong and Ang Tian Se. MAA Reviews, https://www.maa.org/press/maa-reviews/fleeting-footsteps-tracing-the-conception-of-arithmetic-and-algebra-in-ancient-china-revised-edition.

About the Author

For more than five decades, Frank J. Swetz has advocated for the use of history and culture to enliven and deepen the study of mathematics. In particular, he has described how mathematical developments in non-Western societies might be incorporated into the training of secondary school teachers. His books include Was Pythagoras Chinese? An Examination of Right Triangle Theory in Ancient China (The Penn State Press, 1977); From Five Fingers to Infinity: A Journey Through the History of Mathematics (Open Court Publishing, 1994); and Mathematical Expeditions: Exploring Word Problems Across the Ages (Johns Hopkins University Press, 2012).