Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion
Since ancient times, human beings have observed the sky and the movements of the objects—sun, moon, stars, and planets—within it. The regular movements of the sun, moon, and stars provided humanity with its first clocks and calendars, while the irregular but still patterned motions of the planets inspired the idea that their wanderings may influence events here on earth. For these two reasons, ancient civilizations such as the Babylonians, Greeks, Indians, Chinese, and Mayans systematically observed the sky and worked out mathematical schemes to describe what they found there, thereby establishing the science now known as mathematical astronomy.
Ancient mathematical astronomers in Greece and India in particular employed a variety of geometrical models to describe the pattern of movements within the sky, models that were further developed by the Islamic civilization. Computation with these models was a major impetus behind the development of trigonometry, and Copernicus’s attempt to simplify and refine them led to the “sun-centered” geometric model of the Copernican Revolution. Working with these historically significant models—both ancient and Copernican—requires a good knowledge of basic trigonometry, a fact which is left out of most history books, with the result that few people are aware of their mathematical underpinning.
In this paper I describe the prototype of the Greek and Indian models for planetary motion—the basic “epicycle-deferent” model invented by Apollonius of Perga. I show how to find the parameters of this basic model and how to use the model to compute planetary positions. We shall see that trigonometry is exactly the ingredient that makes such geometric models—both ancient and Copernican—quantitatively useful.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Introduction
Since ancient times, human beings have observed the sky and the movements of the objects—sun, moon, stars, and planets—within it. The regular movements of the sun, moon, and stars provided humanity with its first clocks and calendars, while the irregular but still patterned motions of the planets inspired the idea that their wanderings may influence events here on earth. For these two reasons, ancient civilizations such as the Babylonians, Greeks, Indians, Chinese, and Mayans systematically observed the sky and worked out mathematical schemes to describe what they found there, thereby establishing the science now known as mathematical astronomy.
Ancient mathematical astronomers in Greece and India in particular employed a variety of geometrical models to describe the pattern of movements within the sky, models that were further developed by the Islamic civilization. Computation with these models was a major impetus behind the development of trigonometry, and Copernicus’s attempt to simplify and refine them led to the “sun-centered” geometric model of the Copernican Revolution. Working with these historically significant models—both ancient and Copernican—requires a good knowledge of basic trigonometry, a fact which is left out of most history books, with the result that few people are aware of their mathematical underpinning.
In this paper I describe the prototype of the Greek and Indian models for planetary motion—the basic “epicycle-deferent” model invented by Apollonius of Perga. I show how to find the parameters of this basic model and how to use the model to compute planetary positions. We shall see that trigonometry is exactly the ingredient that makes such geometric models—both ancient and Copernican—quantitatively useful.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - The Wandering Stars
To understand what a planetary model does, we must first consider the sky at night. In gazing at the nighttime sky, ancient people noticed that the stars occur in distinct groupings, which we call constellations. One well-known constellation is the Big Dipper; if one “connects the dots” formed by the stars of the Big Dipper, the resulting shape looks like a large ladle, or “dipper.” The Big Dipper is actually part of a larger constellation known as Ursa Major, or the Great Bear. Another well-known constellation is Orion, whose belt forms three bright stars visible in the winter sky of the northern hemisphere.
As the earth moves around the sun, constellations move around in the sky, sometimes disappearing from view for weeks or months. Even in the course of a single night, they can be observed to change their position as the earth rotates. Ancient people observed these changes and noticed a very important fact—while constellations do move around in the sky, they never change their size or shape. The Big Dipper always looks the same, no matter when we observe it, although it might be in a different part of the sky or pointing in a different direction.
The fact that constellations do not change their size or shape led ancient people to notice that some “stars” do not stay put within any constellation. These “stars” became known as “wandering stars,” or planets. We now know them to be the five planets of our solar system that are visible to the naked eye—Mercury, Venus, Mars, Jupiter, and Saturn.
The ancient Babylonians were the first to pay careful attention to the wanderings of the planets. Ancient people believed the planets to be heavenly bodies whose motions could influence events on earth; thus it was important to chart and predict their motions through the stars. By carefully observing their wanderings over many years, the ancient Babylonians observed that all the planets seem to move along roughly the same path through the stars. That path became known as the ecliptic.
To visualize the ecliptic we can think of the sky as a huge “celestial sphere” with the earth in the center and with the stars plastered to its inside surface (see Figure 1 below). At any one time only half the sphere is visible; the other half is below the horizon. Under this model the ecliptic is a great circle on the sphere; at any one time half of it stretches across the sky in a rough east to west direction.

Figure 1
The ecliptic is more accurately defined as the apparent annual path of the sun through the stars. As everyone knows, the sun rises in the east and sets in the west every day. This apparent motion of the sun is caused by the earth’s west to east rotation. However, there is a second motion of the sun that is not as obvious, but was observed and tracked by the Babylonians. If you go out in the early evening and observe the western horizon just after sunset when the stars are first becoming visible, there will be some constellation of stars there. (In reality, the air pollution and artificial light of modern times obscure the stars at the horizon just after sunset, but in ancient times, from whence these ideas originate, these stars were easier to see.) If you did this over the course of a complete year, you would observe that the constellation in that part of the sky at that time of the evening changes. In ancient times you would see (roughly) the constellation Capricorn in January, Aquarius in February, Pisces in March, Aries in April, Taurus in May, Gemini in June, Cancer in July, Leo in August, Virgo in September, Libra in October, Scorpio in November, and Sagittarius in December. These, of course, are the well-known signs of the zodiac; in fact, this is where the zodiac comes from. The sun, moon, and planets all appear to wander through the constellations of the zodiac. More specifically, the sun completes one cycle through the zodiac in one year, moving in an apparent circle around the earth. This circle is the ecliptic.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - The Wandering Stars (continued)
A little thought will convince you that the apparent motion of the sun around the ecliptic is caused by the earth’s actual yearly revolution of the sun. The idea is illustrated in Figure 2. [To view the animation for this and the succeeding figures, click on "Figure x" below the illustration. You will then open a new window with an animated version of the Figure. You will need to have Java enabled on your computer.]
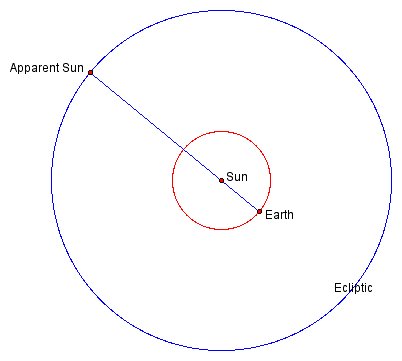
In Figure 2, the blue line is the line of sight from the earth to the sun, and the “apparent sun” is the apparent position of the sun within the far distant background of the stars. Animating the figure we see that as the earth revolves around the sun, the blue line of sight rotates around the earth, which causes the apparent sun to revolve around the blue circle (the ecliptic). Hence, as seen from earth, the sun appears to circle the earth around the ecliptic once a year.
The planets also appear to circle the earth around the ecliptic, each at its own rate, moving generally from west to east. The average time it takes for one complete cycle ranges from one year for Mercury and Venus to almost 30 years for Saturn. However, the motion of a planet along the ecliptic is far from uniform. This is illustrated by animating Figure 3, which simulates the 12-year journey of Jupiter around the ecliptic.
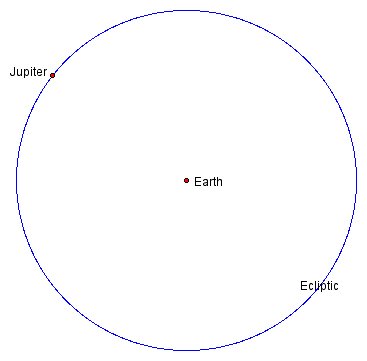
As Figure 3 illustrates, as a planet travels around the ecliptic, it periodically slows down, stops, and reverses its direction for a short time, moving from east to west instead of west to east. These so-called retrograde motions were observed and studied by the ancient Babylonians.
In order to quantify their observations of planetary motions, the Babylonians divided the ecliptic into 360°, with 0° taken to be the apparent location on the ecliptic of the sun at the spring equinox. The measure in degrees of a planet’s apparent position on the ecliptic is called its longitude. Using astronomical instruments, it was possible for early astronomers to measure a planet’s longitude and thereby track its motion around the ecliptic though time. A planetary model, as conceived of by the Greeks, is a geometric model that replicates this observed motion of the planet around the ecliptic. Such a model must agree with observational data and in particular must adequately account for the planet’s retrograde motions.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - The Basic Modern Model
We pause here in our account of history to give the basic modern explanation for the motions of the planets described in Section 3. As seen from earth, the motion of the planet along the ecliptic is actually a combination of two motions—the real motion of the planet around the sun, and an apparent motion caused by the motion of the earth. These two motions combine to give the west to east circuit of the ecliptic with retrograde motions described in Section 3. Animating Figure 4 illustrates how this happens for the planets Mercury and Venus, the so-called “inner planets” which lie between the earth and the sun.
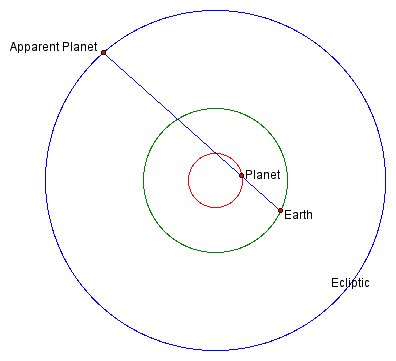
Figure 5 illustrates the situation for the “outer planets” including Mars, Jupiter, and Saturn.
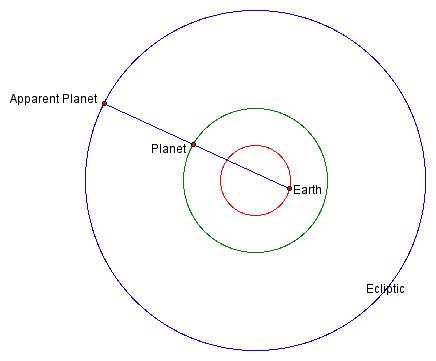
Note that in both models the earth’s orbit and the planet’s orbit are in the same plane (the plane of the ecliptic). The blue line segment represents the line of sight from the earth to the planet; the intersection of this line with the ecliptic thus represents the apparent position on the ecliptic of the planet as seen from earth. This point is called the “apparent planet.”
This account of planetary motions is, of course, a simplified version of what actually occurs. Planets and the earth orbit the sun in ellipses, not circles, and change speeds as they travel, unlike the uniform speed shown in the animation. Also their orbits are not all in the same plane, but are slightly inclined to each other. However, the ellipses are almost circles, the speeds are almost uniform, and the planes are almost all the same. Thus this simple model gives a crude approximation to actual planetary motions, and is a good start towards a more accurate one. Furthermore, these considerations do not affect the basic explanation given by the model for the apparent motions of the planets including retrograde motions.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - The Basic Ancient Model
The modern explanation described in Section 4 is an example of a geometric model for the motions of the planets—the apparent motions along the ecliptic are explained in terms of actual motions on geometric objects (circles). However, this explanation assumes a moving earth, which contradicts both intuition and “common sense.” Using just the evidence of their ordinary senses, it appeared to ancient people, as it does to us, that the earth is motionless while everything else in the sky—sun, moon, planets, and stars—moves in various ways. The ancient Greeks and Indians therefore sought a geometric model that accounted for the motions of the planets while leaving the earth at rest.
Such a model was probably first invented in the third century B.C.E. by the great Greek geometer Apollonius of Perga [13, p. 262]. (Apollonius is best known for his study of the conic sections—parabolas, ellipses, and hyperbolas—found in his book Conics.) In Apollonius’s model the planet moves uniformly around a circle called an epicycle, while the center of the epicycle moves uniformly around the earth on a larger circle called the deferent. Figure 6 illustrates this basic model; as can be seen, the model can generate retrograde motions quite well.
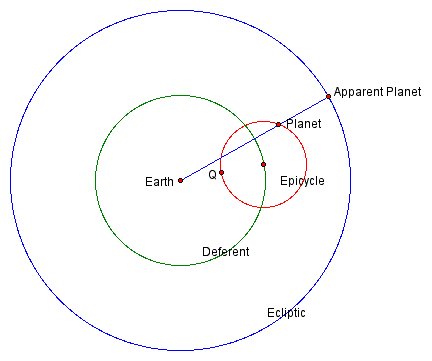
In circular motion, the time it takes an object to complete one full revolution around its circle is called its period. There are two periods in the basic ancient model: the period of the epicycle center as it revolves around the deferent, and the period of the planet as it revolves round the epicycle. The first period represents the time it takes the planet, on average, to return to the same point of the ecliptic; this is called the sidereal period. The latter period could be taken to be the time between successive returns of the planet to the point Q in the diagram; as such it represents the time between the middles of successive retrograde motions. This period is called the synodic period.
The basic model has three parameters. These are: r/R, where r is the radius of the epicycle and R is the radius of the deferent; the sidereal period T; and the synodic period S. In Figure 6, dragging the points labeled r/R, T, and S will change these parameters. The reader should observe how varying these quantities changes the planet’s motion, in particular the spacing, duration, or size of the retrograde arcs.
Like the basic modern model, this ancient model gives only a crude approximation to the motions of the planets. For example, the model implies that a planet’s retrograde arcs are all evenly spaced on the ecliptic, and are all of the same length. Because of the careful and systematic observations of the Babylonians, ancient astronomers knew this not to be the case: a planet’s retrograde arcs vary in both spacing and length. To account for irregularities like this, the actual models used by the Greeks and Indians incorporated other geometric devices into the underlying blueprint of the basic model. Nonetheless, we will use the basic model to derive an approximate quantitative description of the motions of the planets. In this way we will gain some insight into the mathematical techniques of early planetary theory and in particular its use of trigonometry.
To convert the basic model into a quantitative description of a planet’s motion, specific values for the parameters must be derived. We carry out this task in Sections 6 and 7.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Planetary Periods
The Babylonians found good approximations to the sidereal and synodic periods of each planet by carefully observing the patterns of the planet’s motion over a length of time. For example, they observed that Mars regularly completes one sidereal cycle (around the ecliptic) in a little under 2 years, and one synodic cycle (from one retrograde motion to the next) in a little over 2 years. Hence, the sidereal period of Mars is a little under two years and its synodic period is a little over 2 years.
By observing the planet over a longer length of time, more accurate estimates were obtained. For example, in just under 15 years, Mars completes 7 synodic cycles and just under 8 sidereal cycles; thus the sidereal period of Mars is approximately 1.9 years and its synodic period is approximately 2.1 years. After a little more than 17 years, Mars completes 8 synodic cycles and a little more than 9 sidereal cycles; adding this 17-year cycle to the previous 15-year cycle, we might expect to get a more accurate 32-year cycle: Mars completes 15 synodic cycles and just about 17 sidereal cycles in just about 32 years. Direct observation reveals that this is indeed the case, giving the more accurate estimates of 2.13 years and 1.88 years for the synodic period and the sidereal period, respectively.
In a similar manner, adding the 32-year cycle to the 15-year cycle results in a still more accurate 47-year cycle, and the 47-year cycle added to the 32-year cycle gives the even more accurate 79-year cycle: Mars completes approximately 42 sidereal cycles and 37 synodic cycles in approximately 79 years. This last 79-year cycle gives a synodic period of 2.135 years and a sidereal period of 1.881 years.
Cyclical data for each planet is given below. This data was known to the Babylonians and was used by Claudius Ptolemy in the Almagest to initially develop his models [13, pp. 151-152]. In his final models, Ptolemy modified the data somewhat to give better long-term results [20, pp. 423-424].
Mercury: 46 sidereal cycles and 145 synodic cycles in 46 years
Venus: 8 sidereal cycles and 5 synodic cycles in 8 years
Mars: 42 sidereal cycles and 37 synodic cycles in 79 years
Jupiter: 6 sidereal cycles and 65 synodic cycles in 71 years
Saturn: 2 sidereal cycles and 57 synodic cycles in 59 years
By observing the times of the equinoxes and solstices, ancient astronomers were able to approximate the number of days in one year. The modern value for this is well known: there are 365.24 days in one year. This important parameter together with the data above determines the sidereal and synodic rates of motion (in degrees per day) for each planet. For example, Mars completes 42 sidereal cycles in 79 years. Therefore in 79 years it completes 42 x 360° in 79 x 365.24 days. Dividing, this gives a sidereal rate of 0.524°/day.
Table 1 gives the sidereal and synodic periods and rates of motion for each planet determined by the cyclical data listed above.
|
|
Sidereal Period T (in years) |
Sidereal Rate (°/day) |
Synodic Period S (in years) |
Synodic Rate (°/day) |
|
Mercury |
1 |
0.986 |
0.317 |
3.11 |
|
Venus |
1 |
0.986 |
1.6 |
0.616 |
|
Mars |
1.88 |
0.524 |
2.14 |
0.462 |
|
Jupiter |
11.8 |
0.0833 |
1.09 |
0.902 |
|
Saturn |
29.5 |
0.0334 |
1.04 |
0.952 |
Table 1
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Determining r/R
In addition to the periods of the planets, ancient astronomers observed two other gross features of their motions—the lengths and times (durations) of their retrograde arcs. For a single planet the length and time of its retrograde arcs vary somewhat; the following table gives approximate average values that appear to be close to those known to Ptolemy [18].
|
|
Length |
Time (days) |
|
Mercury |
12° |
20 |
|
Venus |
15° |
40 |
|
Mars |
16° |
72 |
|
Jupiter |
10° |
120 |
|
Saturn |
7° |
140 |
Table 2
Revisiting Figure 6, we see that fixing T and S and varying the ratio r/R changes the lengths of the retrograde arcs. Larger values of r/R result in larger retrograde arcs, while smaller ones result in smaller arcs or sometimes none at all. This suggests that data like that found in Table 2 might be used to determine the ratio r/R.
According to [18], ancient astronomers may have used such data, plus a little trigonometry, to find an initial estimate of the ratio r/R for each planet. For the outer planets—Mars, Jupiter, and Saturn—this method of determining r/R is somewhat similar to the method actually used by Ptolemy in the Almagest. For the inner planets—Mercury and Venus—Ptolemy in the Almagest computed this parameter by a quite different method which involved using the planet’s so-called “greatest elongation” from the sun.
To compute r/R by using the data in Table 2, we start at a time when the epicycle center, the planet, and the earth are all in a straight line, with the planet P at the point P[0] on the epicycle (see Figure 7).
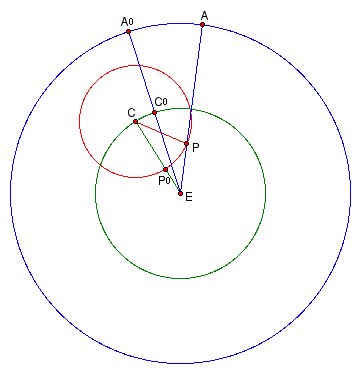
In the figure, C0 is the location of the epicycle center at this time and A0 is the location of the apparent planet on the ecliptic. At this point the planet is in the middle of its retrograde arc. Animating Figure 7 shows the planet’s motion from the middle of the retrograde arc until the end. At that point C represents the new location of the epicycle center and A represents the new location of the apparent planet. Trigonometry now enters the picture, as r is side CP and R is side EC of triangle ECP; thus to find the ratio r/R, we must solve the triangle ECP for the ratio of its sides CP/EC.
Since the planet moves uniformly on the epicycle, the arc P0P has measure equal to the synodic rate of the planet (see Table 1 in Section 6) multiplied by half the time of its retrograde arc given in Table 2 above. Since arc P0P and angle P0CP have the same measure, this determines angle C in triangle ECP. Similarly, since the epicycle center moves uniformly on the deferent, arc C0C has measure equal to the sidereal rate multiplied by half the time of the retrograde arc. This determines angle C0EC which forms part of angle E in triangle ECP. Finally, arc A0A is by definition half of the planet’s retrograde arc; thus its measure is known from Table 2 above. This determines angle A0EP; adding this to angle C0EC gives angle E in triangle ECP. Altogether we have found angles C and E in triangle ECP; subtracting their sum from 180° determines angle P. Using the Law of Sines we can now solve the triangle for the ratio CP/EC.
As an illustration of this method we show the computations for the planet Mars, using modern trigonometry and notation.
Example: Mars
From Table 2, we get the retrograde arc data: (1/2)length = 8° and (1/2)time = 36 days.
From Table 1, we find that the synodic rate is 0.462°/day and the sidereal rate is 0.524°/day.
Angle ECP = arc P0P = (synodic rate) x (1/2)time = 16.6°.
Angle C0EC = arc C0C = (sidereal rate) x (1/2)time = 18.9°.
Angle A0EP = arc A0A = (1/2)length = 8°.
Angle PEC = the sum of angles C0EC and A0EP = 26.9°.
Angle CPE = 180° minus the sum of angles PEC and ECP = 136.5°.
By the Law of Sines, r/R = CP/EC = sine(PEC)/sine(CPE) = 0.66.
Exericise: Use the data in Tables 1 and 2 to find r/R for Mercury, Venus, Jupiter, and Saturn. (Answers are given in Table 3 of Section 8.)
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Summary: Parameters of the Basic Ancient Model
Table 3 exhibits the parameters for the basic ancient model that are computed by using the data and techniques described in the previous two sections.
|
|
Sidereal Period T (in years) |
Synodic Period S (in years) |
r/R |
|
Mercury |
1 |
0.3 |
0.37 |
|
Venus |
1 |
1.6 |
0.72 |
|
Mars |
1.9 |
2.1 |
0.66 |
|
Jupiter |
11.8 |
1.1 |
0.19 |
|
Saturn |
29.5 |
1.0 |
0.11 |
Table 3
With these parameters in hand, it is fun to revisit Figure 6 and feed in the appropriate parameters for each planet. Running the animation at the same speed for each planet allows us to compare the various journeys of the planets as they make their way around the ecliptic. From the swift movements of Mercury to the lumbering journey of Saturn, we see the same general pattern with important individual differences.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Calculating Planetary Positions
Now that we have determined the parameters of the basic ancient model for each planet, we can calculate planetary positions. This involves solving the same triangle CEP that we solved to find the parameter r/R.
First we must initialize the model. Figure 8 shows two hypothetical positions of the planet: one at the initial time T0 and another at a future time T.
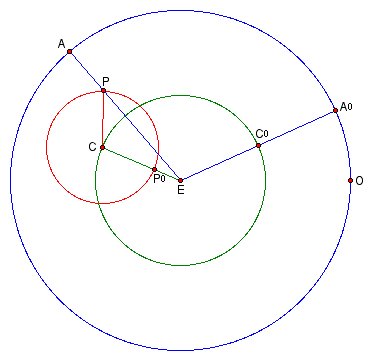
At time T0 the planet is in the middle of its retrograde arc and occupies the position P0 on the epicycle. The epicycle center is at the point C0 on the deferent, and the apparent planet is aligned with the center at the point A0 on the ecliptic. At this point one uses an astronomical instrument to observe the longitude of the planet. This gives the position in degrees of the apparent planet on the ecliptic, as measured from the point O on the ecliptic, and initializes the model. (Recall from Section 3 that O is the apparent position of the sun on the ecliptic at the spring equinox.)
The planet's longitude at time T is calculated by finding the measure of arc A0A and adding it to the planet's longitude at T0. To do this we must solve triangle ECP for angle PEC. A sample calculation for Mars is shown below. For simplicity in the calculation we take as our unit of measure the radius R of the deferent; with this unit of measure, r is equal to the parameter r/R. The solution presented makes use of modern trigonometry and notation.
Example: The motion of Mars over the course of a retrograde arc is observed with an astronomical instrument, and it is determined that the middle of the arc occurred at longitude 40º. Find the longitude of Mars 250 days later.
Solution:
By Table 1 in Section 6. we know that the Sidereal rate is 0.524º/day and the Synodic rate is 0.462º/day. R = 1 unit (assumed); r = r/R = 0.66 by Table 3 in Section 8.
The longitude at T0 is given as 40º and the elapsed time from T0 to T is given as 250 days.
At T, arc C0C = (sidereal rate) x (elapsed time) = (0.524) x (250) = 131º and
arc P0P = (synodic rate) x (elapsed time) = (0.462) x (250) = 115.5º.
Angle ECP = arc P0P = 115.5º.
EC = R = 1 unit; CP = r = 0.66.
By the Law of Cosines, PE = Ö(EC2 + CP2 - 2EC(cos(ECP))) = 1.416
By the Law of Sines, sin(PEC) = CP sin(ECP) / PE= 0.421, so that angle PEC = arcsin(0.421) = 25º.
Arc A0A = arc C0C - angle = 131º - 25º = 106º.
Longitude at T = Longitude at T0 + arc A0A = 40º + 106º = 146º.
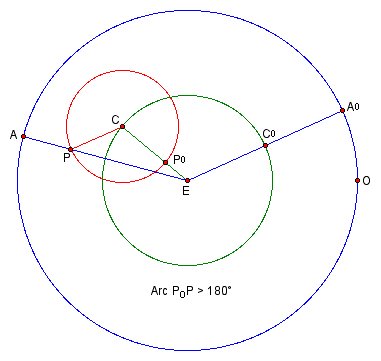
Note that all arcs are measured in a counterclockwise direction, and, by adding or subtracting multiples of 360º if necessary, have measure between 0º and 360º. Figure 9 shows a configuration in which arc P0P is greater than 180º; this may be helpful to some readers in completing the following exercises.
Exercises
1. The motion of Jupiter over the course of a retrograde arc is observed with an astronomical instrument, and it is determined that the middle of the arc occurred at longitude 345º. Find the longitude of Jupiter 430 days later.
2. The motion of Mars over the course of a retrograde arc is observed with an astronomical instrument, and it is determined that the middle of the arc occurred at longitude 130º.
a. Find the longitude of Mars 500 days later.
b. Find the longitude of Mars 500 days before the observation.
3. The motion of Saturn over the course of a retrograde arc is observed with an astronomical instrument, and it is determined that the middle of the arc occurred at longitude 210º. Find the longitude of Saturn 1000 days later.
Answers
1. 15º
2. a. 52º b. 208º
3. 248º
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Trigonometry in the Basic Modern Model
Trigonometry enters into the basic modern model in essentially the same way as the ancient one. This is because the two models are “equivalent”: given a particular planet, the ancient epicycle-deferent model for the planet’s motion gives the same longitudes as the modern model based on a moving earth.
Figure 10 demonstrates the equivalence for an outer planet. (To see things more clearly, start your exploration of this figure by hiding the triangles.)
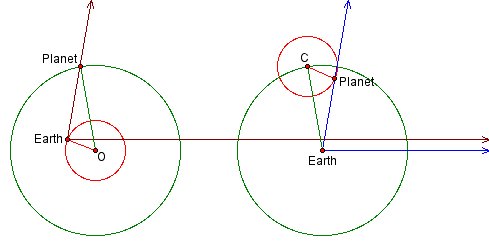
In each model the longitude of the planet is given by the rotating angle centered at the earth; the sides of the angle are brown in the modern model on the left and blue in the ancient model on the right. In both cases one side of the angle points in a fixed direction from the earth, while the other side passes through the planet. In the modern model the earth moves in a circle, bringing the vertex of the angle with it; in the ancient model the earth and the vertex remain stationary. When set in motion, the corresponding sides of the angles remain parallel to each other; thus the longitude is the same under both models. Superimposing the two models, we see that the motion of the planet around its epicycle reflects the earth’s actual motion, while the motion of the center around the deferent reflects the planet’s actual motion.
Figure 11 demonstrates the equivalence for an inner planet. Note that here the role of the epicycle and the deferent are reversed: the epicycle reflects the planet’s actual orbit of the sun, while the deferent reflects the earth’s.
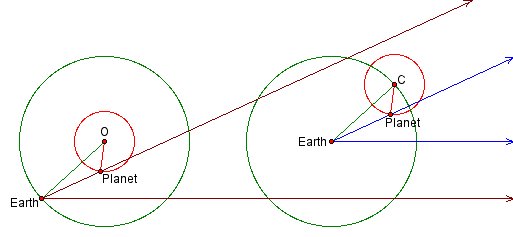
Showing the triangles in the two figures, we can gain some insight into how this equivalence affects computations within the basic modern model. In the ancient model, known information about the motion of the planet around its epicycle and the point C around the deferent translates into information about the triangle formed by the earth, the planet, and the epicycle center C; trigonometry then allows one to calculate parameters and planetary positions. In the modern model, the mathematical situation is virtually unchanged. Known information about the motions of the earth and planet around their circles translates into information about the triangle formed by the earth, the planet, and the center of the earth’s orbit O; parameters and planetary positions are then calculated by solving this triangle. In each case the crucial step is the ability to solve a triangle, a step that is impossible without trigonometry.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Concluding Remarks
In this article we have explored the basic epicycle-deferent model for planetary motion and its modern equivalent, and have seen how trigonometry enables these models to give a quantitative description of the wanderings of the planets. The planetary positions computed by such simple models are not very accurate, and even early astronomers were well aware of their limitations; as a result, they modified their models with various geometric devices. These modifications did make the models more accurate; for example, errors in Ptolemy’s models for the outer planets amounted to no more than one degree in predicted longitude [14, p. 323]. At the same time, however, such modifications led to the need for even more trigonometric computations. In the final planetary models of both Ptolemy and Copernicus, for example, not one but at least three triangles had to be solved to compute a single planetary position.
The models described in this article represent just one application of trigonometry to early astronomy; there are many others. However, considering just this one application, we have seen that the trigonometry required in early astronomy included knowledge of both the Law of Sines and the Law of Cosines (or their equivalents), as well as the ability to compute at least the sine (or its equivalent) of any given angle. In response to such demands, the ancient Greeks developed a rudimentary form of trigonometry called the “theory of chords.” Along with Euclid’s geometry, this theory enabled astronomers to solve triangles (using procedures equivalent to the Laws of Sines and Cosines), and to compute the “chord” of any given angle (equivalent to twice the sine of half the angle) in one-half degree increments. However, the theory of chords was clumsy and difficult to work with, and as techniques of astronomy improved, so did the need for more and more accurate and efficient trigonometric computations. As a result, the theory of chords was developed by Indian, Islamic, and later European mathematicians and astronomers into much of the basic trigonometry that we know today.
While the physics they were based on was faulty, pre-Copernican models of planetary motion nonetheless gave a successful mathematical description of the known cosmos of the time. In the 16th century Copernicus’s attempt to simplify these models and make them more accurate led to a series of events that changed the course of human history—the Copernican Revolution. It is fair to say that without the study of triangles in the sky, that revolution may never have occurred.
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Bibliography and Further Reading
Good accounts of early astronomy can be found in [5], [11], and [19]; [11] and [19] also contain sections on early trigonometry. Presentations of the history of astronomy and trigonometry within the more general context of the history of mathematics can be found in [2] and [7]. For discussions of early astronomy focusing mainly on planetary models and the Copernican Revolution, see [3] and [10]. The various websites listed below offer Java animations of many of the geometric models of early astronomy, as well as general information pertaining to the subject. The primary source for Greek astronomy and trigonometry is Ptolemy’s Almagest; [20] is a good English translation. Finally, it should be mentioned that [8] contains classroom resource materials utilizing various ideas from the history of trigonometry and astronomy.
1. Scott R. Anderson, “Introduction to Astronomy, Lecture 5: The Motion of the Planets,” Open Course, http://www.opencourse.info/astronomy/introduction/05.motion_planets/index.html, accessed September 5, 2008.
2. Carl B. Boyer, A History of Mathematics, 2nd edition, revised by Uta C. Merzbach, John Wiley & Sons, New York, 1991.
3. Michael J. Crowe, Theories of the World from Antiquity to the Copernican Revolution, 2nd revised ed., Dover Publications, Mineola, 2001.
4. Dennis Duke, “Ancient Planetary Model Animations,” http://people.scs.fsu.edu/~dduke/models.htm, accessed September 5, 2008.
5. James Evans, The History and Practice of Ancient Astronomy, Oxford University Press, New York, 1998.
6. Andres Vargas Idrobo, “Ptolemy’s Theory of Superior Planets,” http://faculty-staff.ou.edu/B/Peter.Barker-1/HSCI3013/planet.html, accessed September 5, 2008.
7. Victor J. Katz, A History of Mathematics: An Introduction, 3rd ed., Addison-Wesley, Boston, 2008.
8. Victor J. Katz and Karen Dee Michalowicz, eds., Historical Modules for the Teaching and Learning of Mathematics (on CD-ROM), Mathematical Association of America, Washington DC, 2004.
9. Rosemary Kennett, “Epicycles and Deferents,” http://www.phy.syr.edu/courses/java/demos/kennett/Epicycle/Epicycle.html, accessed September 5, 2008.
10. Thomas S. Kuhn, The Copernican Revolution: Planetary Astronomy in the Development of Western Thought, Harvard University Press, Cambridge, 1957.
11. C. M. Linton, From Eudoxus to Einstein: A History of Mathematical Astronomy, Cambridge University Press, Cambridge, 2004.
12. Craig Sean McConnell, “Models of Planetary Motion from Antiquity to the Renaissance,” http://faculty.fullerton.edu/cmcconnell/Planets.html, accessed September 5, 2008.
13. Otto Neugebauer, A History of Ancient Mathematical Astronomy, Part 1, Springer-Verlag, New York, 1975.
14. Robert R. Newton, The Crime of Claudius Ptolemy, Johns Hopkins University Press, Baltimore, 1977.
15. Scott C. Smith, “Retrograde Motion,” http://www.lasalle.edu/~smithsc/Astronomy/retrograd.html, accessed September 5, 2008.
16. “Ptolemaic System Generator,” Nebraska Astronomy Applet Project, http://astro.unl.edu/naap/ssm/animations/ptolemaic.swf, accessed September 5, 2008.
17. “Ptolemy’s Epicycle,” http://www.sciences.univ-nantes.fr/physique/perso/cortial/bibliohtml/epiclc_ja.html, accessed September 5, 2008.
18. Noel M. Swerdlow, “The Empirical Foundations of Ptolemy’s Planetary Theory,” Journal for the History of Astronomy, 35 (2004), 249-271.
19. Hugh Thurston, Early Astronomy, Springer-Verlag, New York, 1994.
20. G. J. Toomer, transl., Ptolemy’s Almagest, Princeton University Press, Princeton, 1998.
21. Greg Van Brummelen, “Animations of Ptolemy’s Planetary Models,” http://faculty.bennington.edu/~gvanbrum/, accessed September 5, 2008.