The Weierstrass Approximation Theorem

Throughout this article, f will be a continuous real-valued function on an interval [a, b], and p will be a real polynomial that approximates f on [a, b].

The first step is to show that polynomial approximations exist to arbitrary accuracy. This is the conclusion of the famous Weierstrass approximation theorem, named for Karl Weierstrass.

Theorem 1 (Weierstrass)

Let f be a continuous real-valued function on the closed interval [a, b]. Then there is a sequence of real polynomials p₁, p₂, ... that converge uniformly to f.

The proof of the Weierstrass theorem by Sergi Bernstein is constructive: it defines explicitly a sequence of polynomials that converge to f. Suppose that f is a continuous real-valued function defined on [0, 1] (there is no loss of generality in restricting the interval in this way). Define the Bernstein polynomials on f by:

Theorem 2 (Bernstein)

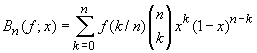
The Bernstein polynomials B_n(f; x) converge uniformly to f on [0, 1].

The following applet shows the progress of successive Bernstein polynomials in approximating a continuous function. You may select one of the three predefined functions, or you may sketch a function by dragging the mouse from left to right over the plotting region. The applet constructs a piecewise linear function from the pixels selected. Press Start to plot the Bernstein polynomial of degree 1. The Next 1 and Next 10 buttons increase the degree by 1 or by 10, up to a maximum degree of 500.

As you can see by trying out the applet, the Bernstein polynomials provide high-quality approximations, but they converge very slowly to their target function. To find good polynomial approximations of smaller degree, we look to other methods. In particular, we look to see how well we can approximate a function with a polynomial of fixed degree.

2. The Weierstrass Approximation Theorem

Theorem 1 (Weierstrass)

Theorem 2 (Bernstein)