- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
History of Mathematics: Highways and Byways

Publisher:
Mathematical Association of America
Publication Date:
2010
Number of Pages:
330
Format:
Hardcover
Series:
Spectrum
Price:
66.50
ISBN:
9780883855621
Category:
Monograph
The Basic Library List Committee suggests that undergraduate mathematics libraries consider this book for acquisition.
[Reviewed by , on ]
James T. Tattersall
04/20/2010
The authors, now at the Alexandre Koyré Center for Research in the History of Science and Technology in Paris, have produced a delightful and informative overview of some aspects of the history of mathematics aimed at students, teachers, and to a general audience. Their book was first published in France in 1982 under the title Routes et dédales (Paths and Mazes) and reissued in 1986 with the title Une histoire des mathématiques: Routes et dédales. The approach is refreshing and makes for enjoyable reading.
Each of the eight chapters contains chronological vignettes that could be used to supplement the mathematical content in secondary school courses in algebra, geometry, and pre-calculus, or collegiate courses in differential and integral calculus, geometry, modern algebra, and analysis. Each brief capsule is well thought out and often presents fresh interpretations of incidents in the history of mathematics. There are very few students or teachers of mathematics who would not benefit from the authors’ discourses on the development of the calculus and evolution of the theory of functions.
The first chapter consists of a sketch of the history of mathematics from the Egyptians and Greeks to the early nineteenth century and provides an interesting overview of that history. There is an enlightening section on the influence of the Church and scholasticism in the High Middle Ages (C.E. 1100–1300).
There are a few problems. It is not clear why the authors chose to use L´´ as the Greek symbol for 1/2. Some typos have crept in that were not in the original. Three examples:
- The
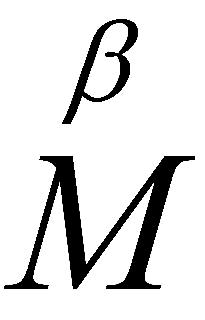 should be
should be 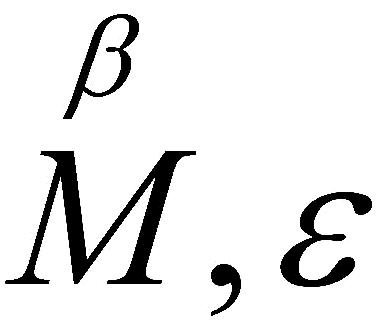
- The table on page 8 gives x as the symbol for 20; it should be κ.
- In the multiplication performed by Eutocius the “819000” should read “819900”.
Notably absent is any discussion on Indian or Chinese contributions to mathematics. The dates for Gerbert, Pope Sylvester II, should be (940–1003). Condorcet’s active role in the French revolutions is mentioned but not the fact that it cost him his life. The AMS was founded in 1894. Its precursor, The New York Mathematical Society, was founded in 1888.
In the second chapter readers will find a succinct account of the Greek mathematics and philosophy as it flourished in Ionia, Athens, and Alexandria. There is a section on Euclid’s Elements and its historical significance. Apollonius’ and Archimedes’ major accomplishments and their significance are discussed. The third chapter consists of a synopsis of development of algebraic notation and the solution of polynomial equations. Major characters include Diophantus, Al-Khwarizmi, Rudolph, Viète, Tartaglia, Cardan, and Abel. There is an informative appendix on construction with a straightedge and compass. It is surprising that the Arabic astronomer more familiarly known as Ulugh Beg is referred to as Ulugh Bek. The fourth chapter introduces the basic concepts of projective geometry, descriptive geometry, geometric transformations, non-Euclidian geometry, and the importance of the Erlanger Program.
In the fifth chapter covers the evolution of the integral and differential calculus beginning with the contributions of the Greek and including a masterful account of the importance of Cauchy’s and Weierstrass’s work on rigor in analysis. Barrow is referred to as Newton’s teacher, which was not the case. The sixth chapter contains an excellent account of the development of the concept of a function. In the last two chapters, the relevance of complex numbers and the notion of a group are introduced. These two concepts are used to illustrate how several different branches of mathematics can be integrated.
A list of ten English references is provided. However, five of the eight chapters in the French edition included a section on original source material and other references, mainly in French or German, which had guided the authors in their research for the book. These are missing in this edition, making it difficult, without access to an earlier edition, to look up the source of a quote or locate the page where the name of a particular mathematician appears. There are some instances where a geometric diagram would have been helpful to the reader and the use of terminology which may appear strange to readers. For example, on Page 184, triangle ABC has area A, and regions in the plane are often referred to as surfaces. In addition, there is only a brief account of the importance of number theory and topology.
However, all the quibbles mentioned above are minor. The major shortcoming of this edition of the book is an inadequate index. The two very useful indices in the French edition, consisting of about 350 terms and proper names, have been shortened in this edition to a single index of less than 100 items.
All things considered, the book was an absolute pleasure to read. The authors should be commended for producing such a splendid addition to literature in the history of mathematics. The translator, Sanford Segal, should be praised for his expertise in making it possible for English readers to access to this remarkable work.
Jim Tattersall is Professor of Mathematics at Providence College, in Providence, RI.
I. Landscapes:
The first ancient civilizations
Greek logistic
Arab civilization
The golden age of scholasticm
The diffusion of new ideas in the sixteenth century
First progress: arithmetic and algebra
The mathematization of science in the 17th century
The mathematical eighteenth century
The new condition of mathematical work in the nineteenth century
II. A moment of rationality: Greece
III. The constitution of classical algebra
IV. Pragmatic origins of Geometry
V. Limits: From the unconceived to the concept
VI. The concept of function and the development of analysis
VII. At the crosswords of algebra, analysis and geometry: complex numbers
VIII. The emergence of algebraic structures.
- Log in to post comments




