Restricted Patterns of the Past, Present and Future

Speaking at the MAA Carriage House on May 31, Zvezdelina Stankova (Mills College and UC Berkeley) aimed to not only educate listeners about restricted patterns, but also spark their interest in the topic.

“My hope is some of you will get so excited that you will solve some of the open problems that we will hear about today,” she said at the outset of her Distinguished Lecture, “Restricted Patterns of the Past, Present, and Future.”

Even stating those problems takes some doing, of course, so Stankova set to work.

How to Avoid a Permutation

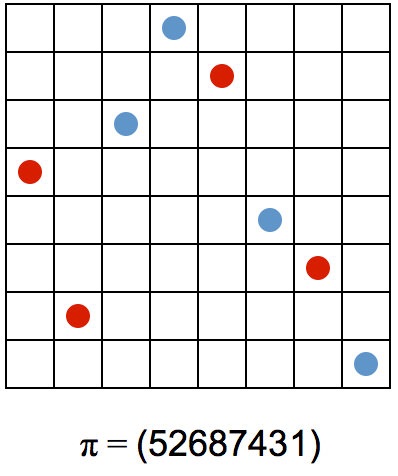
At the heart of restricted patterns is the notion of one permutation avoiding another, and visualization aids in understanding this. A permutation of length n can be represented by placing dots in certain positions in an \(n\)-by-\(n\) grid.

Consider, for example, the permutation \(τ\) = (3142). To visualize this permutation, draw a 4-by-4 grid and place a dot three rows up in the first (leftmost) column, another dot in the first (bottom) row of the second column, another dot in the fourth row of the third column, and a final dot in the second row of the fourth column, as shown below left. Convince yourself that the permutation \(π\) = (52687431) is represented by the grid on the right.

Now \(π\) is said to avoid \(τ\) if \(π\) contains no subsequence of the same type as \(τ\). Here \(π\) does not avoid \(τ\) because \(π\) contains the subsequence (5273), the elements of which have the same greater than/less than relationships the elements of \(τ\) do. (Nor is this the only such subsequence. Find another.)

Mathematicians focus their energies, however, on permutations that do avoid a given permutation. Initially mind-bending perhaps, but actually simpler.

“There is only one way you can avoid something,” Stankova explained. “You are containing it zero times. But if you contain something, you can contain it several times. And then the question becomes very complicated.”

So the main set of interest in the study of restricted patterns is \(Sn(ω)\), the set of \(ω\)-avoiding permutations of length \(n\).

The Big Questions

Once mathematicians conceived of these sets, of course, the impulse to count and classify took over. How many \(ω\)-avoiding permutations of length \(n\) are there for various \(ω\)’s and \(n\)’s? Can permutations be grouped based on how restrictive they are, that is, how hard they are to avoid?

This second question can be more precisely formulated in terms of Wilf equivalence (named for the late great Herbert Wilf). Two permutations \(τ\) and \(π\) are Wilf equivalent if they are equally restrictive, if, that is, for any permutation of length \(n\), the same number of permutations avoid \(τ\) as avoid \(π\). So, can we classify permutations up to Wilf equivalence?

The problem is “still wide open,” Stankova told the Carriage House audience, “but I will tell you how wide open it is.”

\(S9\) Anyone?

A good first step in classifying permutations is to exploit symmetry (which is, helpfully, particularly salient in grid representations of permutations).

Given, for example, a gridded permutation that avoids 321, flipping the permutation across the vertical will yield a permutation that avoids 123. Thus there is a one-to-one correspondence between the permutations that avoid 321 and those that avoid 123, and \(Sn(321)\) and \(Sn(123)\) are Wilf equivalent. Similar arguments can be made using rotations.

Another strategy for establishing Wilf equivalence involves constructing permutation trees and showing that the trees are isomorphic.

Using such techniques and building upon them, Stankova and her fellow restricted pattern enthusiasts have classified \(S3\) through \(S8\) (all permutations, that is, of length 3 through 8).

“So it is now your turn,” Stankova charged her Distinguished Lecture listeners. “\(S9\).”

Enticement

And there’s plenty of motivation to dig in, according to Stankova. Besides being “beautiful” and “mind-boggling,” restricted patterns have connections to the Catalan numbers and riffle shuffling and stack-sortability. Sets of avoiding permutations have cropped up in seemingly unrelated areas of mathematics, indexing interesting subclasses of Schubert varieties, for instance. Many outstanding questions exist, among them: If two permutations are known not to be equally restrictive, is it possible to determine that one is more restrictive than the other?

Stankova’s first exposure to what was then called “forbidden subsequences” came in 1991—in a van en route to the University of Minnesota Duluth for (eventual MAA president) Joe Gallian’s REU. The subject was in its infancy then, and Stankova could find no recent literature to supplement the Ph.D. thesis Gallian handed her while still in transit.

Since 2003, however, there has been sufficient interest in and work on permutation patterns to warrant an annual international conference, convening in such enticing locales as Florence, Paris, New Zealand, and, in June 2016, Washington, D.C.

But even with mathematicians across the globe applying themselves to the problems posed by restricted patterns, “there are still too many conjectures to prove,” Stankova told her Washington, D.C., audience on May 31. “So it’s really up to you to pick up on this topic.”

Katharine Merow is a freelance writer living in Washington, D.C.