Mathematics in medieval Europe was not just the purview of scholars who wrote in Latin, although certainly the most familiar of the mathematicians of that period did write in that language, including Leonardo of Pisa, Thomas Bradwardine, and Nicole Oresme. These authors – and many others – were part of the Latin Catholic culture that was dominant in Western Europe during the Middle Ages. Yet there were two other European cultures that produced mathematics in that time period, the Hebrew culture found mostly in Spain, southern France, and parts of Italy, and the Islamic culture that predominated in Spain through the thirteenth century and, in a smaller geographic area, until its ultimate demise at the end of the fifteenth century. These two cultures had many relationships with the dominant Latin Catholic culture, but also had numerous distinct features. In fact, in many areas of mathematics, Hebrew and Arabic speaking mathematicians outshone their Latin counterparts. In what follows, we will consider several mathematicians from each of these three mathematical cultures and consider how the culture in which each lived influenced the mathematics they studied.

We begin by clarifying the words “medieval Europe”, because the dates for the activities of these three cultures vary considerably. Catholic Europe, from the fall of the Western Roman Empire up until the mid-twelfth century, had very little mathematical activity, in large measure because most of the heritage of ancient Greece had been lost. True, there was some education in mathematics in the monasteries and associated schools – as Charlemagne, first Holy Roman Emperor, had insisted – but the mathematical level was very low, consisting mainly of arithmetic and very elementary geometry. Even Euclid’s Elements were essentially unknown. About the only mathematics that was carried out was that necessary for the computation of the date of Easter.

Recall that Spain had been conquered by Islamic forces starting in 711, with their northward push being halted in southern France in 732. Beginning in 750, Spain (or al-Andalus) was ruled by an offshoot of the Umayyad Dynasty from Damascus. The most famous ruler of this transplanted Umayyad Dynasty, with its capital in Cordova, was ‘Abd al-Raḥmān III, who proclaimed himself Caliph early in the tenth century, cutting off all governmental ties with Islamic governments in North Africa. He ruled for a half century, from 912 to 961, and his reign was known as “the golden age” of al-Andalus. His son, and successor, al-Ḥakam II, who reigned from 961 to 977, was, like his father, a firm supporter of the sciences who brought to Spain the best scientific works from Baghdad, Egypt, and other eastern countries. And it is from this time that we first have mathematical works written in Spain that are still extant.

Al-Ḥakam’s son, Hishām, was very young when he inherited the throne on the death of his father. He was effectively deposed by a coup led by his chamberlain, who soon instituted a reign of intellectual terror that lasted until the end of the Umayyad Caliphate in 1031. At that point, al-Andalus broke up into many small Islamic kingdoms, several of which actively encouraged the study of sciences. In fact, Sā‘id al-Andalusī, writing in 1068, noted that “The present state, thanks to Allah, the Highest, is better than what al-Andalus has experienced in the past; there is freedom for acquiring and cultivating the ancient sciences and all past restrictions have been removed” [Sā‘id, 1991, p. 62].

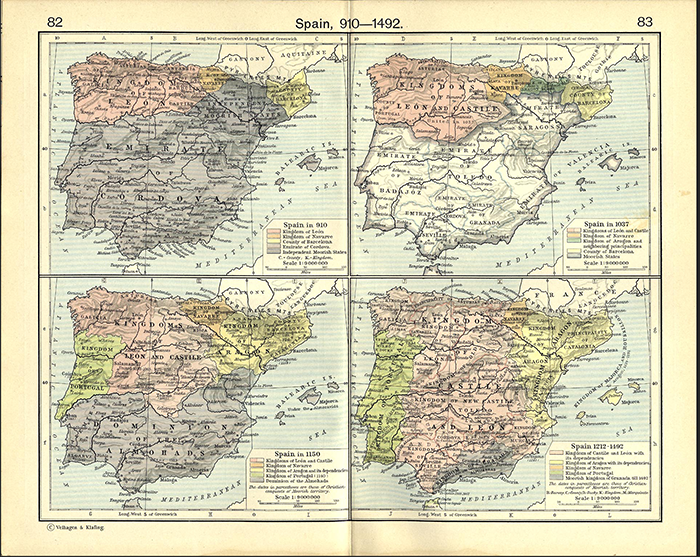
Figure 1. Maps of Spain in 910 (upper left), 1037 (upper right), 1150 (lower left), and 1212-1492 (lower right)

Meanwhile, of course, the Catholic “Reconquista” was well underway, with a critical date being the reconquest of Toledo in 1085. Toledo had been one of the richest of the Islamic kingdoms, but was conquered in that year by Alfonso VI of Castile. Fortunately, Alfonso was happy to leave intact the intellectual riches that had accumulated in the city, and so in the following century, Toledo became the center of the massive transfer of intellectual property undertaken by the translators of Arabic material, including previously translated Greek material, into Latin. In fact, Archbishop Raymond of Toledo strongly encouraged this effort. It was only after this translation activity took place, that Latin Christendom began to develop its own scientific and mathematical capabilities.

But what of the Jews? There was a Jewish presence in Spain from antiquity, and certainly during the time of the Umayyad Caliphate, there was a strong Jewish community living in al-Andalus. During the eleventh century, however, with the breakup of al-Andalus and the return of Catholic rule in parts of the peninsula, Jews were often forced to make choices of where to live. Some of the small Islamic kingdoms welcomed Jews, while others were not so friendly. And once the Berber dynasties of the Almoravids (1086-1145) and the Almohads (1147-1238) from North Africa took over al-Andalus, Jews were frequently forced to leave parts of Muslim Spain. On the other hand, the Catholic monarchs at the time often welcomed them, because they provided a literate and numerate class – fluent in Arabic – who could help the emerging Spanish kingdoms prosper. By the middle of the twelfth century, most Jews in Spain lived under Catholic rule. However, once the Catholic kingdoms were well-established, the Jews were often persecuted, so that in the thirteenth century, Jews started to leave Spain, often moving to Provence. There, the Popes, in residence at Avignon, protected them. By the end of the fifteenth century, the Spanish Inquisition had forced all Jews to convert or leave Spain.

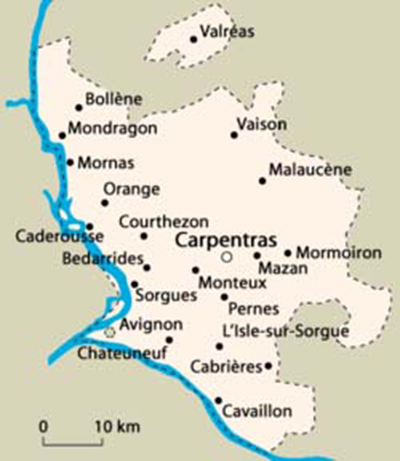
Figure 2. Papal territories in Provence

It was in Provence, and later in Italy, that Jews began to fully develop their interest in science and mathematics. They also began to write in Hebrew rather than in Arabic, their intellectual language back in Muslim Spain.  

As noted above, it was the rulers of the individual Islamic states in al-Andalus who decided whether to support mathematics and other sciences. So why would a ruler support a mathematician? Generally, it was because he felt that the mathematician could contribute to the wealth and, perhaps, the prestige of the kingdom. And a mathematician definitely needed support. Certainly, he could have a non-mathematical position that earned him a living, but it was better for scientific work if he were given the funds so he could spend sufficient time on mathematics. There were no institutional structures in Islamic Spain, or indeed in the Islamic world in general, that would allow a mathematician to flourish. There were no universities and the madrasas, in general, provided instruction in the religious sciences, but not the secular ones.

So, we are left with looking at the relationship between a ruler and a mathematician. We will consider four examples. The first is Abū ‘Abdullah Muḥammad ibn ‘Abdūn (923-976), a mathematician who was born and taught mathematics in Cordova, the capital of the Umayyad caliphate. He became a physician through his studies in the East and then returned to Cordova as the physician of the caliph, al-Ḥakam II. His only known mathematical work is On measurement, of which only one copy survives. Many of the methods in this treatise can be found in texts written in ancient Babylon. In fact, ibn ‘Abdūn’s treatise marks the extension of a pre-algebraic tradition of measuring surfaces from the eastern Islamic lands to al-Andalus and, then, to the Maghreb. This treatise is basically a practical manual, and not a theoretical one. It is, therefore, not surprising that the author of such a treatise would be supported. This was mathematics that could be used.

At the beginning of the manuscript of this treatise ibn ‘Abdūn is referred to as muhandis and faraḍī. The first denotes someone involved with measuring (theoretical or practical, e.g. surveying), and the second denotes a specialist in the arithmetical procedures necessary to calculate the legal heirs’ shares of an inheritance according to Islamic law. The treatise consists of a collection of problems in which the author presented algorithms for finding areas or lengths. He began with rectangles, squares, triangles, and parallelograms, then moved to circles, where he used the standard approximation of 22/7 for \(\pi\) in his calculations. But he also showed knowledge of the old methods of solving what we would call quadratic equations when he asked the reader to find certain lengths given information about areas or diagonals.

In these problems, he did not use the al-Khwārizmīan terminology of “thing” for the unknown and māl (treasure) for square. He simply converted all his measurements to numbers and gave an algorithm for finding the answers. The algorithms are like those from ancient Mesopotamia and are ultimately based on manipulation of geometric figures. But ibn ‘Abdūn left out any justification at all, as in the following examples:

If you are told, “We add the sides and the area and it is one hundred forty, what are the sides?” The calculation is that you add up the number of the sides, which is four, and take its half, two. Multiply it by itself, it is four. Add it to one hundred forty, which is one hundred forty-four. Then take the root of that, twelve, and take away from it half of the four and the remainder is equal to each of its sides.

If you are told that the diagonal is ten and one side exceeds the other by two, what are its two sides? The way to calculate this is that you multiply the diameter by itself, which is one hundred, and you multiply the two by itself, which is four, and you subtract it from one hundred. The remainder after that is ninety-six. You take half of that, which is forty-eight, which is the area. Now it is as if you are told, “A rectangle, whose length exceeds its width by two, and its area is forty-eight. What is each of the sides?” So, you work as we described to you [earlier], and you will hit the mark, Allah willing. [Katz et al, 2016, 452]

A century after ibn ‘Abdūn, we find another mathematician involved in a very practical subject, spherical trigonometry, the key to the understanding of astronomy. This was ibn Mu‘ādh al-Jayyānī, whose work, the Book of Unknowns of Arcs of the Sphere, written probably in the middle of the eleventh century, is the earliest extant work on pure trigonometry that was not written as an introduction to a work on astronomy. The last part of ibn Mu‘ādh’s name suggests that he was from Jaén in Andalusia. He is known to have been a qādī (religious judge) and in fact came from a family whose members included several such learned officials. Thus, given that he was active after the end of the Umayyad caliphate, he was probably supported by the ruler of one of the small Islamic kingdoms in the south of Spain. What we do not know is how ibn Mu‘ādh learned his trigonometry. His work is similar to material that had been widely discussed in eastern Islam, but nothing of his book points to any particular known eastern source.

Despite this work being a purely mathematical one, ibn Mu‘ādh obviously intended it to help in the study of astronomy. But it was not an elementary work. As he wrote in the preface,

In this book, we want to find the magnitudes of arcs falling on the surface of the sphere and the angles of great arcs occurring on it as exactly as possible, in order to derive from it the greatest benefit towards understanding the science of celestial motions and towards the calculation of the phenomena in the cosmos resulting from the varying positions of celestial bodies. … So, we present something whose value and usefulness in regard to understanding this [subject] are great. As for premises that were derived by scholars who preceded us, we give just the statements, without proof, so that we may arrive at acknowledgement of their proof. … We have written our book for those who are already advanced in geometry, rather than for beginners. [Katz et al, 2016, 503]

There are many possible starting points for the basic results of spherical trigonometry. Ibn Mu‘ādh chose as his starting point the transversal theorem, a theorem well-known from Greek times, although written then in terms of chords rather than Sines (where we use “Sine” to denote the medieval sine, the length of a line segment in a circle of a given radius). This theorem shows the relationship among certain ratios of Sines of arc segments in a figure consisting of four intersecting great circle arcs. Given this result and various similar ones, ibn Mu’adh then set out his goal for the book:

We say that there are two kinds of things found in a triangle, sides and angles. There are three sides and three angles, but there is no way to know the triangle completely, i.e. [all] its sides and its angles, by knowing only two of the six. Rather, from knowing only two things, be they two sides or two angles or one side and one angle, it [the triangle] is unspecified. For it is possible that there are a number of triangles, each of which has those [same] two known things, and so one must know three things connected with it [the triangle] to obtain knowledge of the rest. Thus, it is impossible to attain all of it knowing less than three members: three sides, three angles, two sides and an angle or two angles and a side. [Katz et al, 2016, 504]

In other words, ibn Mu’adh’s goal was to solve spherical triangles, given the knowledge of three of the six “things”. On the way to doing this, he proved various important results. For instance, he showed that if the ratio of the Sines of two arcs is known as well as their difference (or their sum), then the arcs are determined. He also demonstrated the spherical law of Sines, “a theorem of great usefulness and abundant benefit in general.”

In any triangle whose sides are arcs of great circles, the ratio of the Sine of each of its sides to the Sine of the opposite angle is a single ratio [Katz et al, 2016, 512].

After a long discussion of the properties of right spherical triangles, including results involving Cosines as well as Sines, Ibn Mu‘ādh systematically showed how to solve triangles, when any set of three “things” is known, often by dropping perpendiculars and then using the properties of right triangles. Probably the most difficult of the solutions to accomplish is when all three angles are known, obviously a result that has no parallel in plane trigonometry. (See [Katz et al, 2016, 518-520] for the details.)

The two works mentioned above were reasonably practical. After all, measurement was necessary in all sorts of contexts, and spherical astronomy was important for astronomy, which was in turn necessary for calculating the direction and times of prayer. In fact, in a short work ibn Mu‘ādh described how to find the qibla, the direction of prayer. On the other hand, he also wrote a very theoretical treatise on ratios, a work explaining in detail Euclid’s definition of ratio in Book V of the Elements. (See [Katz et al, 2016, 468-478, 530-533] for these two works.) Other mathematicians too worked on quite theoretical material.

For example, consider ibn al-Samḥ (984-1035), who lived in Cordova toward the end of the Umayyad caliphate, when that government was in turmoil. He was a student of the famous astronomer, Maslama al-Majrītī (950-1007), and wrote on astronomy, astrology and mathematics. Evidently, however, he earned his living as a practicing physician. Here, we look at his geometrical text, The Plane Sections of a Cylinder and the Determination of their Areas, which today only survives in a Hebrew translation by Qalonymos ben Qalonymos of Provence.

Ibn al-Samḥ’s treatise is in two parts. In the first part, he introduced a figure constructed by what he called a “triangle of movement” and then considered an oblique section of a right circular cylinder, which he knew was an ellipse. He constructed the “triangle of movement” by fixing one side of a triangle and moving the intersection of the other two sides continuously in such a way that the sum of their lengths is constant, although the lengths of each will vary as their intersection moves.

Figure 3. The "triangle of movement" of ibn al-Samḥ of Cordova

From a modern point of view, this is one of the construction methods for an ellipse, but ibn al-Samḥ needed to show that this figure and the section of the cylinder share the same properties and therefore are the same figures. In the second part, Ibn al-Samḥ determined the area of the ellipse by relating its area to that of its inscribed and circumscribed circles. To do this, however, he found various ratios among the ellipse, its inscribed and circumscribed circles, and the major and minor axis. For example, he proved that the ratio of the inscribed circle to the ellipse is the same as the ratio of the minor to the major axis. Also, the ratio of the inscribed circle to the ellipse is the same as the ratio of the ellipse to the circumscribed circle.

Finally, the proposition giving the area of an ellipse is phrased in a way that echoes Proposition 1 of Archimedes’ Measurement of the Circle, each expressing the area of a curved figure (an ellipse in the one case, a circle in the other) in terms of a certain right triangle. Further, he actually calculated the area:

Every ellipse is equal to the right triangle of which one of the sides containing the right angle is equal to the circumference of the inscribed circle and of which the second side is equal to half of the greatest diameter. It results from what we have established that if we take five sevenths and one half of one seventh of the smallest diameter, and multiply this by the greatest diameter, we obtain the area of the ellipse. [Katz et al, 2016, 467]

Another important mathematician from Spain at this time was Al-Mu’taman Ibn Hūd (d. 1085). Until recently his works were thought to have been lost, but in the late 1980s Professors Ahmed Djebbar and Jan Hogendijk discovered manuscripts of his extensive survey of the mathematics of his time, his Kitāb al-Istikmāl (Book of Perfection). Ibn Hūd had planned for the book to have two “genera” but he had only finished the first when he became King of Saragossa, one of the small Islamic kingdoms on the peninsula, in 1081 and evidently had no time to write the second before he died four years later. Ibn Hūd had an elaborate division of his “genera” into species, subspecies, and sections. The work, definitely not intended for beginners, sheds unexpected light on the mathematics of Ibn Hūd’s time and is a fascinating blend of mathematics from Greek and Arabic sources, as well as what appear to be some original contributions of ibn Hūd himself. Obviously, given his position as a member of the dynasty that ruled Saragossa from 1038 to 1110, he was free to study whatever mathematics he wished. He clearly had the means to immerse himself in translated Greek mathematics and then to work on problems coming from these Greek sources. Consider these samples from the Book of Perfection:

[Heron’s Theorem:] [For] each triangle the ratio of the surface that is made of half the sum of its sides by the excess of that half over one of the sides to the surface of the triangle is as the ratio of the surface of the triangle to the surface that is made from the excess of half the sum of the sides over one of the two remaining sides by [the excess over] the other [Katz et al, 2016, 479].

Ibn Hūd’s proof was different from the one given by Heron. It made central use of the incircle of the triangle, the triangle whose center is the intersection of the angle bisectors of the triangle and which is tangent to all three sides.

Ibn Hūd also stated and proved a theorem thought to have been first stated by the Italian geometer Giovanni Ceva in 1678. 

[Ceva’s Theorem:] In every triangle in which from each of its angles a line issues to intersect the opposite side, such that the three lines meet inside the triangle at one point, the ratio of one of the parts of a side of the triangle to the other [part], doubled with the ratio of the part [of the side] adjacent to the second term [of the first ratio] to the other part of that side is as the ratio of the two parts of the remaining side of the triangle, if [this last] ratio is inverted, and conversely [Katz et al, 2016, 483].

Probably the greatest accomplishment of ibn Hūd was his study of a famous problem in geometrical optics generally referred to as “Alhazen’s Problem”, which concerns reflection in mirrors whose surfaces are curved. (Alhazen is the Latin version of the name of ibn al-Haytham (965-1039), who discussed this problem is his famous work on optics.) Suppose one is given a spherical or conical mirror, concave or convex, and an object (thought of as being a point) visible in the mirror to an observer (represented by another point). The question is: At what point on the mirror will the observer see the object? As part of his solution to this problem, ibn al-Haytham gave six difficult geometrical lemmas, which were adapted by ibn Hūd in his Istikmāl. In some cases ibn Hūd followed ibn al-Haytham’s ideas, but in a number of cases he introduced new techniques, which simplified and shortened ibn al-Haytham’s proofs.

It is clear that the men we have discussed were quite able mathematicians. How did a mathematician operate in Muslim Spain? In general, as we suggested earlier, a mathematician needed another career to provide support, such as medicine or as a religious functionary, or else he needed to be supported by – or in the case of ibn Hūd, actually was – the ruler of the state in which he lived. There was no structure in this society that could support a steady flow of intellectual development, such as a university. If one wanted to study a particular field, one had to find an expert with whom to study. Since Spain at this time was far from the center of the Islamic domains, someone who wanted to study some advanced mathematical topic had to go to the east – to Egypt or Persia or Baghdad. But there certainly were people able to produce interesting mathematics in Muslim Spain. As we have seen in our examples, they restricted themselves to certain topics, in particular, geometry and trigonometry. Obviously, both of these were based on Euclid’s Elements, which had been translated many times into Arabic, beginning in the ninth century, while the latter topic was necessary for astronomy. But Muslim mathematicians had also read Archimedes, Apollonius, and Ptolemy, among other Greek authors. They certainly absorbed the Greek notion of mathematical proof, and we see this demonstrated in treatises written in Spain. Sā‘id names many other mathematicians active in al-Andalus up to the mid-eleventh century besides the ones mentioned above, but in virtually all cases, their fields of mathematical interest were geometry and trigonometry.

Although Muslim authors in the East were developing algebra during the period of Islamic rule in Spain, there is little evidence that any algebraic work more advanced than that of al-Khwārizmī was studied in Spain. In fact, the algebra that did appear in Spain is more closely related to the older geometric strain of the subject than to the more modern use of unknowns. Furthermore, even though Averroes (1126-1198) translated and commented extensively on the work of Aristotle, and his translations were quite influential later in Catholic Europe, Muslim mathematicians did not attempt to develop any of the mathematics implied by some of Aristotle’s physical ideas.  

There is little evidence that there were any religious restrictions to the practice of mathematics in Spain. So, the reasons why one topic or another was studied or not were practical, such as the availability of teachers, or, more simply, had to do with the inclinations of a particular mathematician.

To complete the story, note that after the Battle of Navas de Tolosa, in 1212, in which Catholic armies defeated the Almohads, the Muslims rapidly lost control of most of Spain. In fact, Cadiz and Cordoba were conquered by the Catholics in 1236 and Seville in 1248. Muslim Spain was then reduced just to Granada, a province in which little mathematics was done in the next two hundred years. That is not to say that Muslims in the West stopped doing mathematics. There was certainly significant mathematics done in the twelfth and thirteenth centuries in North Africa, an area culturally similar to al-Andalus. This work included important contributions to combinatorics in the work of ibn Mun’im (d. 1228) and ibn al-Bannā’ (1256-1321), and the introduction of new algorithms for calculating with the Hindu-Arabic numerals by Abū Bakr Muḥammad al Hassār (12th century), some of whose ideas were taken over by Leonardo of Pisa in his Liber abbaci. (See the article "Moses ibn Tibbon's Hebrew Translation of al-Hassar's Kitab al Bayan" in Convergence.) But the discussion of these works would take us outside of the boundaries of Europe.

There was a significant Jewish community in Spain under Muslim rule and, in many times and places, Jews could integrate into the Muslim society. They often served the rulers in administrative or financial capacities. The Jews became fluent in Arabic and used this language in their intellectual pursuits. However, I am not aware of any mathematical work by Jews until the late eleventh century, by which time Toledo and many other parts of Spain were already in Christian hands. We should emphasize that when Jews were living closed off from their neighbors, their creativity was mainly displayed in interpretations of the Bible and of Jewish law. But once Jews could participate in the general society, as in this time period in Spain, they started to display creativity in other fields, including mathematics.

One of the first known Jewish mathematicians is Abraham bar Ḥiyya of Barcelona (1070-1145), who was a community leader as well as a scholar. His Jewish title was nasi (honorary leader), while his Arabic title was ṣāḥib ash-shurṭa (head of the guard, transliterated in Latin as “Savasorda”), a title he probably received from the ibn Hūd dynasty in Saragossa, where he spent time before that dynasty was overthrown. He wrote on mathematics, astronomy, astrology and philosophy, and is distinguished as the first Jewish scholar in the Arabic speaking world to write on science in Hebrew. This choice of language was, at least in part, due to the lack of access of Jews in Provence, where he visited, to the Arabic language. His work includes translations from Arabic to Hebrew, and he collaborated with Plato of Tivoli on translations into Latin as well.

Bar Ḥiyya’s most important mathematical work was The Treatise of Measuring Areas and Volumes. This book was partially translated into Latin in 1145 by Plato of Tivoli, perhaps with Abraham’s help, and made an impact on European scholarship. The treatise opens with a motivational introduction, stating explicitly that Abraham wrote the book to teach the appropriate geometry necessary for both secular and holy affairs. After presenting versions of the early books of Euclid’s Elements, Abraham proceeded to deal with measurements of squares, rectangles and rhomboids (deriving their areas, sides, diagonals, etc. from each other), and included a geometric treatment of quadratic problems. He continued on to triangles, general quadrilaterals, and circles and then studied measurement of polygons by triangulation before presenting some practical suggestions for measuring sloping and curved lands. There is then a section on division of plane areas, perhaps based on Euclid’s own no longer extant book on the same topic.

This work is not a full scholarly geometry, but a compromise between an introduction to abstract geometry and a measurement manual. It provides a good intuitive introduction to geometrical reasoning and has some problems like those of ibn ‘Abdūn. As we will see later, Leonardo of Pisa seems to have used this book, probably in the Latin translation, as one of the sources of his Practical Geometry. But also, it seems clear that in Abraham’s time, Jews generally did not study abstract subjects. If they were interested in mathematics at all, they tended to concentrate on practical subjects.

We begin with Abraham’s motivations for studying geometry at all:

[The scriptures say] “I the Lord am your God, instructing you for your own benefit, guiding you in the way you should go” (Isaiah 48:17), that is, instructing you in whatever is useful for you, and guiding you on the way you follow, the way of the Torah. From which you learn that any craft and branch of wisdom that benefit man in worldly and holy matters are worthy of being studied and practiced.

I have seen that arithmetic and geometry are such branches of wisdom, and are useful for many tasks involved in the laws and commandments of the Torah. We found many scriptures that require them, such as “In buying from your neighbor, you shall deduct only for the number of years since the jubilee”, and “the more such years, the higher the price you pay; the fewer such years, the lower the price”, followed by: “Do not wrong one another, but fear your God” (Leviticus 25:15-17). But no man can calculate precisely without falsification unless he learn arithmetic. … Moreover, the Torah requires geometry in measuring and dividing land, in Sabbath enclosures and other commandments. … But he who has no knowledge and practice in geometry cannot measure and divide land truly and justly without falsification. … It suffices to note that the blessed God prides himself in this wisdom, as is written: “He stood, and measured the earth” (Habakkuk 3:6) and “Who measured the waters with the hollow of His hand, and gauged the skies with a span” (Isaiah 40:12). So, you see from these writings that the blessed God created his world in well founded and weighed out measurement and proportion. And a man must be like his creator with all his might to win praise, as all scholars agree, so from all this you see the dignity of these branches of wisdom. He who practices them does not practice something vain, but something useful for worldly and holy matters.

Arithmetic, which is useful for worldly matters and crafts as well as for the practice of many commandments, is not difficult to understand, and most people understand it somewhat and practice it, so one does not need to write about it in the holy tongue. Geometry is also as useful for as many matters as arithmetic in worldly matters and commandments from the Torah, but is difficult to understand, and is puzzling to most people, so one has to study and interpret it for land measurement and division between heirs and partners, so much so that no one can measure and divide land rightfully and truthfully unless they depend on this wisdom.

I have seen that most contemporary scholars in Spain and Provence are not skillful in measuring land and do not divide it cleverly. They severely belittle these matters, and divide land between heirs and partners by estimate and exaggeration, and are thus guilty of sin … Their calculation might mete out a quarter to the owner of a third, and a third to the owner of a quarter, and there is no greater theft and falsification. [Katz et al, 2016, 297-298]

Although there are many occasions in the Talmud where approximations are used, Abraham insisted that

Our fathers did not allow us to dismiss calculations, nor steal from heirs, nor give any of them more or less than their fair share …. They warned us and gave us strict orders against stealing and falsifying in measuring land ... [Katz et al, 2016, 298-299]

Thus, Abraham concluded, one needs to study the principles of measurement carefully, so that one calculates shares of heirs correctly. So, unlike ibn ‘Abdūn, Abraham presented careful proofs of his rules for calculation, generally based on the Elements. Consider the following examples:

A square quadrilateral that you take away from the number of its area the number of its four sides, and are left with 21 cubits of its area: what is the area and what is the number of each side of the square? Answer: Divide the number of the sides, which is four, into two. Multiply the two by itself, which is 4. Add this number to the given number that’s left over from the square, and the total is 25. Find the root of 25, which is 5. Add half the sides, which is 2, so the total is 7. This is the side of the square, and its area is 49. He who posed the question subtracted from the area, which is 49, the number of the four sides, each of which is 7 and all four 28, leaving from the square 21, as he told you. [Katz et al, 2016, 300-301]

Figure 4. Bar Ḥiyya’s diagram of a square used to justify an algorithm for calculation

After presenting this algorithm, bar Ḥiyya drew a diagram of the square ABCD, then subtracted off rectangle BEGC with BE of length 4 (i.e., the four sides), leaving a rectangle EADG of area 21. He then divided BE in half at H and quoted Elements II-6 to conclude that the square on HA is the sum of rectangle EADG and the square on HE, that is 25. Therefore, HA itself equals 5 and AB equals 7, as desired.

Figure 5. Circle and triangle used to derive a circle area formula

To measure a circle, Abraham presented the classical result that the area was half the diameter times half the circumference. His proof, depending on decomposing an area into lines that it contains, is evidently original:

We know that if you open the area of the circle on one side, and straighten all the surrounding lines from the external line [circumference] to the center, the lines surrounding the area of the circle will spread and turn into straight lines, decreasing until they turn into a single point, which is the center point. Such is the line ABCD … that I have drawn, where the external is the largest, and the next is smaller than the former but larger than the next, and so on to a point, which creates the form of a triangle. But we have already taught the area of a triangle, which is as the height times half the base, which is half the diameter times half the circumference. [Katz et al, 2016, 306]

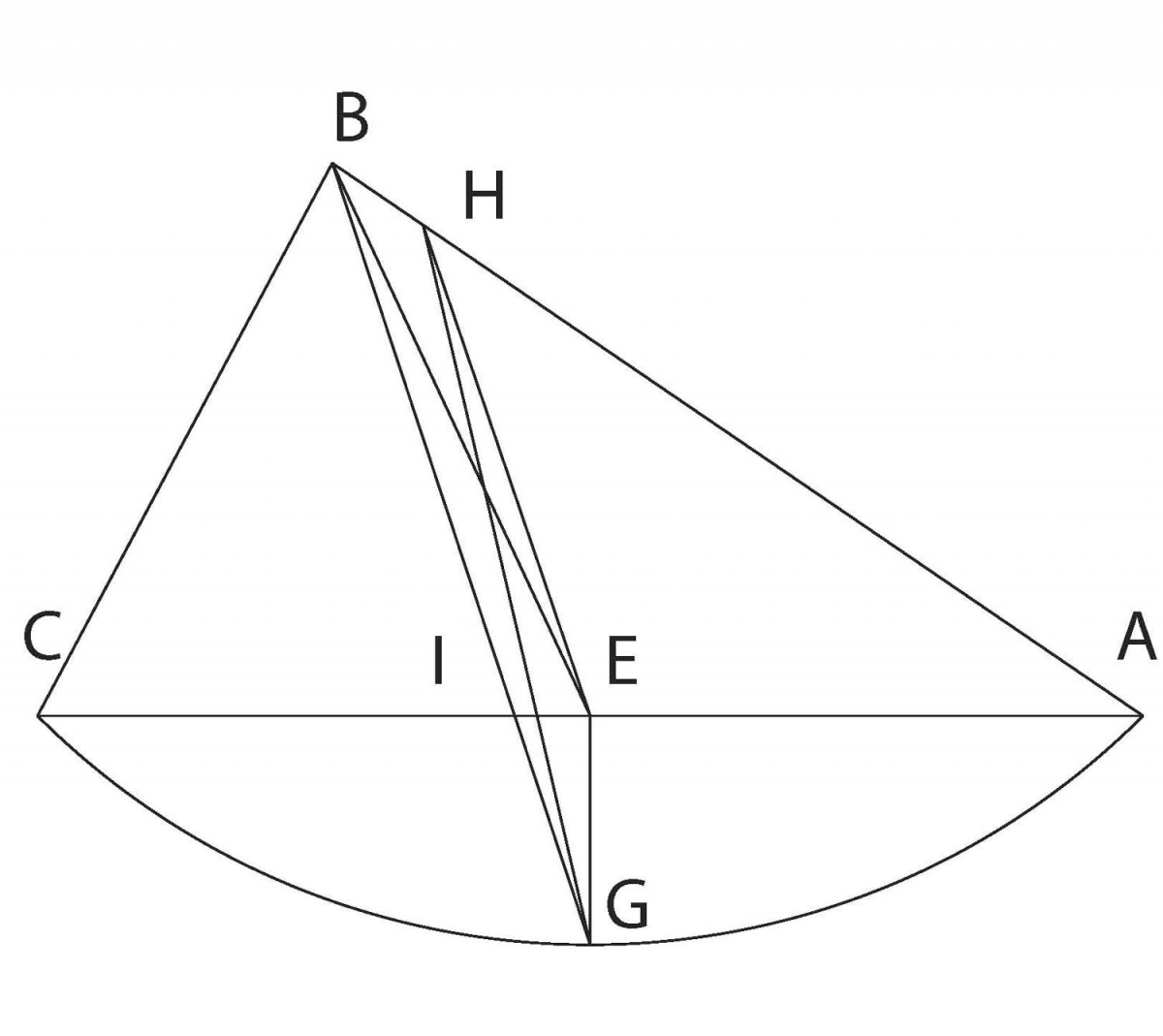
Figure 6. Diagram used to divide a region in half

As an example of dividing fields, Abraham began with a region bounded by an arc of a circle and two straight lines, neither of which are radii. His goal was to find a straight line dividing the region in half. Here E is the midpoint of line AC and EG is perpendicular to AC. Line BG intersects AC at I; then HE is drawn parallel to BG. Then GH divides the region in half. To prove the result, note that BE divides triangle ABC in half, while EG divides segment AECG in half. But triangles GHE and BHE are equal. It follows that region AHG is equal to the sum of triangle ABE and region AEG, so is half of the entire region ABCG.

Abraham ibn Ezra (1090-1167) was a younger contemporary of Abraham bar Ḥiyya. He was born in Tudela, when it was part of the kingdom of Saragossa, but then traveled widely during his adult life. Among his numerous works were books on arithmetic and numerology, as well as a work dealing with astrology which had some interesting combinatorial aspects. As he wrote,

Only when one knows the natural sciences and their proofs, learns the categories that are the ‘guardians of the walls’ taught by the science of logic, masters the science of astronomy with its absolute proofs based on mathematical knowledge, and comprehends the science of geometry and the science of proportions, can one ascend to the great level of knowing the secret of the soul, the secret of the supernal angels, and the concept of the world to come in the Torah, the Prophets, and the sages of the Talmud [Ibn Ezra, 1995, chap. 1].

In other words, the reason for studying mathematics was ultimately to get closer to God. Thus, in general, that mathematics could be studied that was useful toward that end.

In his Sefer ha-Mispar (Book of Number), ibn Ezra expounded on “the science of proportions” as he showed how to use the rule of three to solve problems. He began with methods of calculation, in which he explained the Hindu-Arabic number system, although with Hebrew characters for the digits. But he then showed how to solve numerous commercial problems, such as

Reuven hired Simon to carry on his beast of burden 13 measures of wheat over 17 miles for a payment of 19 pashuts. He carried seven measures over 11 miles. How much shall be paid? [Katz et al. 2016, 231]

Another of the subjects that ibn Ezra thought was useful was astrology. He wrote a series of books on the subject. In particular, in Sefer Haʿolam (Book of the World), ibn Ezra discussed the meaning of celestial conjunctions and aspects. He began by counting all possible conjunctions of the seven known planets, demonstrating some systematic combinatorial reasoning. In order to calculate the number of different sets of n elements out of 7 planets, he used a recursive method, taking partial sums of the sequence 1,2,3,4,5,6,7, then taking partial sums of the sequence of these partial sums, etc.

There are 120 conjunctions [of the seven planets]. You can calculate their number in the following manner: it is known that you can calculate the number that is the sum [of all the whole numbers] from one to any other number you wish by multiplying this number by [the sum of] half its value plus one-half. As an illustration, [suppose] we want to find the sum [of all the whole numbers] from 1 to 20. We multiply 20 by [the sum of] half its value, which is 10, plus one-half, and this yields the number 210. We begin by finding the number of double conjunctions, meaning the combinations of only two planets. It is known that there are seven planets. Thus, Saturn has 6 [double] conjunctions with the other planets. [Jupiter has 5 double conjunctions with its lower planets, Mars has 4, and so on. So we need to add the numbers from 1 to 6]. Hence, we multiply 6 by [the sum of] half its value plus one-half, and the result is 21, and this is the number of double conjunctions. [Katz et al, 2016, 271-272]

Ibn Ezra next found the triple conjunctions, effectively showing that \[C_{7,3}= C_{6,2}+ C_{5,2} +C_{4,2}+ C_{3,2}+ C_{2,2},\] where each \(C_{k,2}\) is shown to be the sum of integers up to \(k-1.\) (For a classroom activity in which students discover this formula, see the Convergence article, "Combining Strands of Many Colors: Episodes from Medieval Islam for the Mathematics Classroom.") Ibn Ezra continued in this manner with quadruple conjunctions and so on until he had found the total of 120 indicated above.

In a further work, the Book of Measure, ibn Ezra gave without proof numerous procedures for determining areas of geometrical figures. Many of these are like material found in bar Hiyya’s work, such as the following problems:

We have added the sides and the area; this gives so much. How much is the side? Take the square of half the number of all the sides [= 4] and add it to the sum [of the area plus the four sides]; subtract from the root of this result half the number of the sides [= 2].

Or, for the circle: If one is dealing with a semicircle, its area is like that of half a circle. If it is smaller or larger [than a semicircle], you must know the diameter of the circle from which the circular segment has been cut, and the length of the chord of the arc and of the sagitta. When you know two of these [three] elements, you can determine the third. Problem: The chord is 8, the diameter, 10. How much is the sagitta? Subtract from the square of half the diameter the square of half the chord; take the root of the remainder, and subtract it from half the diameter; you will find the sagitta [= 2]. [Katz et al, 2016, 289, 291]

Ibn Ezra also presented a table of Sines and later displayed the standard medieval method of using an astrolabe to calculate heights and distances. If one knows the distance to the tall object whose height is to be measured, one uses the astrolabe to measure the proportion of height to distance, from which the height can be calculated. If one does not know the distance, one takes two measurements with the astrolabe from different places and then uses a formula known in China and elsewhere for centuries to calculate the height.

Although ibn Ezra had stated the reasons one could study the sciences, he was not the only one. Baḥya ibn Paqûda, a Jewish philosopher from Saragossa in the mid-eleventh century, wrote the following in his Duties of the hearts:

All departments of science, according to their respective subjects, are gates which the Creator has opened to rational beings, so that they may attain to a comprehension of revealed religion and of the world. But while some sciences satisfy primarily the needs of religion, others are more requisite for the benefit of the world. The sciences specially required for the affairs of the world are the lowest division – namely the science that deals with the natures and accidental properties of physical substances – and the intermediate division – namely the science of mathematics. These two branches of knowledge afford instruction concerning the secrets of the physical world and the uses and benefits to be derived from it, as well as concerning arts and artifices needed for physical and material well-being. But the science that is needed primarily for revealed religion is the highest science, namely the divine science, which we are under obligation to study in order to understand our revealed religion and to reach up to it. To study it, however, for the sake of worldly advantages is forbidden to us. [Freudenthal, 1995, 34]

It was Spanish-born Maimonides (1135-1204), however, whose work was much more important in influencing Jews to study science. Maimonides' family left Spain for North Africa during the reign of the Almohads, but simply settled in another part of the Almohad empire there. Eventually, he traveled to Palestine and then spent the rest of his life in Egypt as a physician to the sultan as well as the most important philosopher in Jewish history. For Maimonides, the study of science and philosophy was actually a religious obligation:

It is certainly necessary for whoever wishes to achieve human perfection to train himself first in the art of logic, then in the mathematical sciences according to the proper order, then in the natural sciences, and after that in the divine science [Freudenthal, 1995, 32].

Maimonides emphasized that it was only truth that counted, and that it did not matter who discovered it. On the other hand, since it was the “divine science” of metaphysics that was the ultimate goal, Maimonides emphasized that science was legitimate and desirable only in so far as it contributed to the divine science. Thus, Medieval Jews were to study mathematics either because they regarded it as essential for metaphysics, preparing the intellect to apprehend abstract truths, or because they needed it as a prerequisite for the study of mathematical astronomy, important for calculating the calendar. 

It seemed clear that the study of Euclid’s Elements was legitimate, and indeed it was widely and continuously studied. Trigonometry, which the Jews learned from the Muslims but to which they made contributions as well, was also a valued study. But somehow, at least in the eleventh and twelfth centuries, it was argued that the study of algebra was pointless, indeed harmful. Medieval algebra was construed as a mere technique, allowing one to solve equations, and as such it had no philosophical value, nor was it apparently of practical use. Abraham ibn Daud of Toledo (1110-1180) wrote:

Among those who spend their time on vanities, thereby depriving their soul of afterlife, is he who consumes his time with number and with strange stories like the following: A man wanted to boil fifteen quarters of new wine so that it be reduced to a third. He boiled it until a quarter thereof departed, whereupon two quarters of the remaining wine were spilled; he again boiled it until a quarter vanished in the fire, whereupon two quarters of the rest were spilled. What is the proportion between the quantity obtained and the quantity sought? [Freudenthal, 1995, 37]

Maimonides himself wrote that the books on conics and on devices (i.e. algebra) and on the science of weights were instances of inquiries that must not be pursued as ends in themselves. They were only worth studying if they helped to “sharpen the intellect” in order to help man achieve knowledge of God. Interestingly, Maimonides himself drew on the demonstrated existence of asymptotes to show that imaginability is not a criterion of existence. “Hear what the mathematical sciences have taught us and how capital are the premises we have obtained from them” [Freudenthal, 1995, 37].

Figure 7. A street sign honoring "Rabi Levi ben Gershom," also known by the acronym "Ralbag"

The foremost medieval Jewish mathematician, Levi ben Gershon (1288-1344), certainly read Maimonides’ works. Yet he interpreted Maimonides differently from most others. Namely, he felt there should be no restriction on what he could write about in science or in mathematics. Because all knowledge of God’s works has religious significance, the acquisition of scientific knowledge about the world is a legitimate end in itself. Thus, Levi explored many different aspects of science and mathematics.

His earliest mathematical work was the Ma’ase Ḥoshev (The Art of the Calculator), a book using Euclidean methodology and, in essence, mathematical induction to prove numerous results in number theory and combinatorics. The first part of the book is very abstract. The earlier propositions deal with such topics as summing integers or squares, while the concluding ones contain important results in combinatorics. Some of the results appear unusual at first glance, such as the following:

To find three numbers such that the sum of the first and third contains the second as a factor as many times as a given number and such that the sum of the second and third contains the first as a factor as many times as a second given number [Katz et al, 2016, 259].

Presumably, this result was included because, in the problem section of the text, Levi wanted to include a numerical version of this challenge and because this is an abstract version of a problem that had appeared earlier in Latin mathematics as the problem of men finding a purse. Also, Levi probably wanted to present combinatorial results because Jews had for centuries been interested in such questions as how many possible words could be formed with the letters of the Hebrew alphabet. Now Levi did not answer such a question directly, but just presented results about combinations and permutations of sets of objects, often proved using what we know as mathematical induction. For example,

When you are given a number of terms and the number of permutations of a second given number from these terms is a third given number, then the number of permutations of the number following the second given number from these terms is the product of the given third number by the excess of the first given number over the second number [Katz et al, 2016, 274].

In modern terms, this result says that \(P_{m,n+1}=(m-n)P_{m,n}.\) This is the inductive step for proving that \[ P_{m,n}=m(m – 1)(m – 2)\cdots(m – k + 1),\] a theorem Levi stated next:

And so, it is clear that the permutations of a given number from a second given number of terms is equal to the number built from consecutive numbers. Their number is equal to the first given number, and the last one is the second given number. [Katz et al, 2016, 275]

(For more problems from Levi ben Gershon's Ma’ase Ḥoshev, see the Convergence article, "The Mathematics of Levi ben Gerson in the Classroom.")

Levi wrote several other mathematical works, two of which were quite theoretical. One of these was a commentary on Euclid’s Elements, in which he spent quite a bit of time giving a proof of Euclid’s parallel postulate. His argument was quite rigorous, but he began with a different postulate:

The straight line which is inclined [to another straight line] approaches [the second line] on the side where an acute angle is formed [with a line crossing both of these that is a perpendicular from the first line to the second] [Katz et al, 2016, 328].

He also wrote a number theory work at the request of a French music theorist. Here he gave a very clever proof of the theorem that a power of 2 must differ from a power of 3 by at least 2, except in the cases 1,2; 2,3; 3,4; and 8,9 [Katz et al, 2016, 277-283].  Presumably this result was of use in music theory, but it is not clear how this would meet Maimonides’ criteria for what could be studied.

There were a few other Jewish mathematicians in Spain and France who also ignored Maimonides’ strictures. For example, consider the work of Abner of Burgos (1270-1348), who lived in Castile. He was originally a Jew, but converted to Christianity and was then known as Alfonso di Valladolid. His most important mathematical work is the Sefer Meyasher ‛aqov (Book of the Rectifying of the Curved), whose aim is to enquire whether there possibly exists a rectilinear area equal to a circular area truly and not by way of approximation. Unfortunately, in the only manuscript we have, the concluding chapter, where the aim was to be accomplished, is missing. But it is the third chapter in which Alfonso considered many interesting geometrical questions related to curves and solids. In particular, Alfonso defined and used the "conchoid of Nicomedes." It is usually accepted that interest in Nicomedes’ work – and his original treatise is lost – was only revived in the late sixteenth century, when it was mentioned and used by Viéte and then later by Descartes and Newton, among others. But, in fact, this curve was discussed by Alfonso, with some important applications. So, what is the conchoid?

Given a straight line (the “ruler” or “canon” AB), a point outside it (the “pole” P), and a distance b, the conchoid of Nicomedes is the locus of all points lying at the given distance d from the ruler AB along the segment that connects them to the pole P. If P is the origin, and AB the line y = a, then the curve is defined by the polar equation r = a sec θ + b. The curve has two branches on opposite sides of the ruler, to which both are asymptotes. The branch passing on the side of the pole has three different distinct forms, depending on the relationship between a and b: If a < b, it has a loop; if a = b, then P is a cusp point; and if a > b, the curve is smooth. The other branch does not change topologically. All versions are shown in the link above.

The importance of the curve to Nicomedes, and later to European mathematicians, was that its use allowed the trisection of an angle, the construction of two mean proportionals between two given line segments, and the doubling of the cube. Alfonso, in fact, demonstrated each of these. His angle trisection is similar, but not identical, to that attributed to Nicomedes, but his construction of two mean proportionals is not found in any of the Greek or Arabic literature, and his use of this to construct the doubled cube is unique. In fact, he constructed a generalization of the Delian problem: To construct a polyhedron which is equal in volume to a given polyhedron and which is similar to a second given polyhedron. To get the doubled cube, simply assume the first given polyhedron is any parallelepiped of volume 2, while the second one is a cube of volume 1. For details, see [Katz et al, 2016, 347-353].

Somewhat later, we find Isaac ibn al-Ahdab (1350-1430) and Simon Motot (mid-fifteenth century) actually studying and writing about algebra. The former was born in Castile, but ended up in Sicily after leaving Spain. He studied the algebra of the Maghrebian mathematician Ahmad ibn al-Banna’ and wrote a detailed commentary on it [Wartenberg, 2015]. Motot lived in Italy and probably learned his algebra in the Italian abacus tradition of his time. His treatise was the first original Hebrew work giving a detailed treatment of the al-Khwārizmīan form of algebra.

Still Levi was, without doubt, the most accomplished Jewish mathematician of the Middle Ages. Even though he went beyond the standard interpretation of Maimonides in deciding that he could study and write on any topic he thought interesting, there were few followers. There was a conflict within the Jewish community regarding what subjects could legitimately be studied, with a sizable proportion of “traditionalists” insisting that only the Torah and Talmud were worthy of study. A further issue was that there was no institutional infrastructure for new students to learn the works of their predecessors. One could always arrange to study privately with an individual, and certainly there were “study groups” established by various people, including Levi himself. But there were no Jewish universities – just as there were no Muslim universities.

Leon Joseph of Carcassonne, who lived around the turn of the 14th-15th centuries in the south of France, wrote about this very issue:

Many years ago I directed my attention toward the study of and research into the profane sciences, which are several in number and nature…. In my eyes, the merits of these sciences were above all praise. ... I therefore followed in the footsteps of the learned men of our own times, … so that they should illuminate my way with the light of their intelligence and understanding …. But I realized that the lack of knowledge that they, and some of my people at this time, found themselves submerged in was great and immense … I perceived that said lack of knowledge on the part of one sector of our nation was by no means strange. Its cause was not unknown and I was not unaware of the Talmudic law which referred to it … Then I heard a voice telling me that there was not one single cause, but many, for the lack and absence of this knowledge among some of our scholars. Sciences defeated them because their subject matter is more rational than in the bosom of our people, and they are as far from them as east is from west, and all the more so from the fundamentals of the Torah and of religious faith. [Those few who did study the sciences] had no right to propound [their knowledge] in the squares and streets, or to discuss it, to show themselves to be favorable toward it, nor to conduct public debates with the aim of reading the complete truth, for knowledge of the truth can only be attained by means of the contrary. …

On seeing the obstacle that these causes represented and aware that the aforementioned sciences were known among the Christians, I said to myself: I shall study their language a little. I shall attend their schools and houses of study. I shall follow their footsteps so that I am able to make use of whatever I might learn from their words. … I found great benefits in this, because in general their discussions on these sciences do not stray from the subject matter; they leave out nothing when it is a question of debating the truth or falsehood of a proposition; they are very rigorous concerning the questions and answers of a debate, which are linked together in such a way as eventually to bring out the truth by means of an analysis of opposing points of view "like a lily among thorns." The way of studying that they practice today as regards these sciences is the same as that followed by our own scholars in earlier times in their study of the science of the Torah. … If these and other sciences should remain beyond our reach, it is not because our intelligence is inferior to that of the Christians, for we possess the same capacity for understanding; indeed, it is the circumstances that have kept us apart, and the memory of them has been erased as a result of exile and repression, and in the same way their pleasure, splendor, and wealth [have been erased]. For this reason, the Christians have continued to advance in the profane sciences while we have continued to lose ground as a consequence of distress and oppression. [Garcia-Ballester et al, 1990, 106-110]

It was, in fact, the existence of universities in Catholic Europe, beginning in the twelfth century, along with the concurrent flood of translations from the Arabic, that provided the impetus for the study and practice of mathematics (and other sciences) in Europe from that time on. However, the first important mathematician in Catholic Europe was Leonardo of Pisa (Fibonacci) (1170-1240), who was not connected to a university. He introduced parts of Islamic mathematics to Europe, after he had accompanied his merchant father on trips to North Africa and elsewhere in the Mediterranean, where he studied with Muslim mathematicians. He mastered the Hindu-Arabic number system as well as the elements of algebra, geometry, and trigonometry. So, in his first book, the Liber Abbaci of 1202, he spent many chapters describing computational methods and then another several chapters showing how to solve numerous types of problems. His methods of solution were varied, including the well-established method of the "rule of three." But since he had learned some algebraic methods as well, he sometimes included these. One of the standard types of problems solved by the rule of three was the “tree problem,” a problem to which he later reduced other types of problems:

There is a tree 1/4 + 1/3 of which lies underground, and it is 21 palms. It is sought what is the length of the tree. Because the least common denominator of 1/4 and 1/3 is 12, you see that the tree is divisible into 12 equal parts. Three plus four parts are 7 parts, and 21 palms; therefore, as the 7 is to the 21, so proportionally the 12 is to the length of the tree. And because the four numbers are proportional, the product of the first times the fourth is equal to the second by the third. Therefore, if you multiply the second 21 times the third 12, and you divide by the first number, namely by the 7, then the quotient will be 36 for the fourth unknown number, namely for the length of the tree; or because the 21 is triple the 7, you have triple the 12, and will have similarly 36. [Katz et al, 2016, 80]

Another standard problem that we have already seen abstractly in the work of Levi ben Gershon, is the problem of men finding a purse:

Two men who had denari found a purse with denari in it; thus found, the first man said to the second, If I take these denari of the purse, then with the denari I have, I shall have three times as many as you have. Alternately, the other man responded, And if I shall have the denari of the purse with my denari, then I shall have four times as many as you have. It is sought how many denari each has, and how many denari they found in the purse. [Katz et al, 2016, 81]

Interestingly, Leonardo did not mention that the problem is indeterminate; he just showed how to find one solution.

Besides these recreational problems, Leonardo devoted many pages to very practical problems such as calculation of profits, currency conversions, alloying of money, barter, determining values of merchandise, and so on. Given that his father was a merchant and that he lived in an Italy where commerce was quickly developing, it is not surprising that these kinds of problems would be of great interest to his readers. Although many of the problems are solved by seemingly ad hoc methods, Leonardo devoted a chapter to explaining the method of false position. Leonardo credited the method to the Arabs, and, of course, this method is found in Arabic texts written in North Africa, such as the work of ibn al-Banna’. This kind of problem is also found in Hebrew works. But Leonardo also devoted the concluding chapter of Liber abbaci to the Muslim method of solving quadratic equations, basically the work due to al-Khwārizmī. He then presented about 100 quadratic problems, taken from the works of such authors as al-Khwārizmī, Abū Kāmil, and al-Karajī.

In his Practical Geometry, Leonardo solved problems like those solved by ibn ‘Abdūn, ibn Ezra, and Abraham bar Ḥiyya. These are generally problems in measurement – of triangles, rectangles, squares, parallelograms, trapezoids, and parts of circles. Just like the earlier authors, sometimes he needed to solve quadratic equations to complete the solutions. From the similarity of some of his problems to those of bar Ḥiyya, in particular, it has been surmised that he had carefully read bar Ḥiyya’s text in its Latin translation.  But it should be noted that Fibonacci did not merely “copy” problems from earlier authors. He may well have read these authors, but he used his own genius to expand on their methods and often to figure out new and ingenious solutions. Thus, he presented a long series of problems on dividing a region into two equal parts. Some of these methods presumably come from the no-longer extant work of Euclid, and some of the methods are found in the work of bar Ḥiyya. But he very carefully explained his procedures and gave careful proofs.

Fibonacci also displayed a talent for abstract mathematics, demonstrated in his Book of Squares, initially prompted by a question from Master John of Palermo to “find a square number from which when five is added or subtracted always arises a square number.” He solved this problem and various associated problems through a series of 24 theorems, all given careful and detailed proofs [Leonardo, 1987]. So, it is clear that Leonardo felt that there was a readership for non-practical problems.

Leonardo was not connected to a university, unlike most of the mathematicians of medieval Europe who followed him. Thus, a few words about the universities are in order here. Well before the end of the twelfth century the Masters at the School of Saint Victor, together with the Masters at the Schools of St. Geneviève and Notre-Dame de Paris, would construct the cradle of the University of Paris. Oxford arose from dissatisfied, mostly English, Masters and students who left Paris for their homeland; similarly, Cambridge was founded from Oxford. The origins of universities in other countries have their own histories, such as the earlier University of Bologna, formed by the students who hired the Masters. The University of Montpellier, among several others, was founded in the thirteenth century. Some schools followed the English model with Masters in charge. Others followed the Italian model with students in charge. Regardless, if there be universities, there must be students, Masters, and a curriculum.

The new curriculum was the gift of the translators, operating mostly in Spain. The curriculum in arts at all the universities was based on the ancient trivium of logic, grammar, and rhetoric and the quadrivium of arithmetic, geometry, music, and astronomy. This study in the faculty of arts provided the student with preparation for the higher faculties of law, medicine, or theology. The centerpiece of the arts curriculum was the study of logic, and the primary texts for this were the logical works of Aristotle, all of which had recently been translated into Latin. The masters felt that logic was the appropriate first area of study since it taught the methods for all philosophic and scientific inquiry. Gradually, other works of Aristotle were also added to the curriculum.  For several centuries, the great philosopher’s works were the prime focus of the entire arts curriculum. Other authors were studied insofar as they allowed one better to understand this most prolific of the Greek philosophers. In particular, mathematics was studied in the universities primarily as it related to the work of Aristotle in logic or the physical sciences. (Algebra, on the other hand, was a non-university subject.) The mathematical curriculum itself – the quadrivium – usually consisted of arithmetic, taken from such works as Boethius’s adaptation of Nicomachus’s Introduction to Arithmetic or a medieval text on rules for calculation; geometry, taken from Euclid and one of the practical geometries; music, taken also from a work of Boethius; and astronomy, taken from Ptolemy’s Almagest and some more recent Latin translations of Islamic astronomical works.

What is important to realize is that, because the universities were corporate bodies generally operating under a royal charter, they were independent of church control. Now, Aristotle’s philosophy did pose problems for Catholic theologians. From Aristotle’s point of view, the world was eternal – it had always existed and would continue to exist. But for Catholics, as for Muslims and Jews, the world had been created by God out of nothing. In fact, in 1277, the Bishop of Paris drew up a list of 219 “errors” in which he alleged that “some scholars of arts at Paris” were transgressing the limits of their own faculty. In particular, he wrote that it was an error to doubt God’s omnipotence; that, in fact, God had absolute power to do whatever He wills, including creating the world out of nothing. Thus, he condemned those ideas that could not be maintained in light of the revealed truth of the Catholic religion.

But this condemnation was too little and too late. The religious elite who dominated intellectual thought had already concluded that rational thought and an empirical methodology were the tools for understanding the world.  In fact, a new canon law had been developed in the twelfth century stating that “anyone (and not just priests) ought to learn profane knowledge not just for pleasure but for instruction, in order that what is found therein may be turned to the use of sacred learning.” [Huff, 1993, 195] In essence, the study of the natural sciences and the pursuit of philosophical truth had become institutionalized in the universities and nothing would disturb this state of affairs. Scientists in Catholic Europe, including mathematicians, were free to study what they wished.

One group of mathematicians who worked at a university were the so-called Oxford calculators, associated with Merton College, Oxford during the fourteenth century. Because they were involved in university teaching, they had to figure out how to explain difficult concepts to students, with the basic method of teaching being disputations with participation from both Masters and students. Thus, they concentrated on logical argument, based on Aristotle’s principles, and then used the argument to try to determine what Aristotle meant in his discussions of physical problems. One of the first of the Mertonians was Thomas Bradwardine (1290-1349).

In his On the Continuum he mentioned five different opinions presented by scholars of his time and earlier:

One must know that the old and modern philosophers have five famous opinions about the composition of the continuum. Some of them, such as Aristotle, Averroes, Algazel [al-Ghazalī] and most of the moderns, argue that the continuum is not composed of atoms, but of parts that can be divided without end. Others say that it is composed of two kinds of indivisibles, because Democritus had assumed that the continuum consists of indivisible bodies. Others say that it consists of points, and this [assumption is divided] into two parts: Pythagoras (the father of this position), Plato, and our contemporary Walter [Chatton] assume that it is composed of a finite number of indivisibles, but others say that [it is composed] of an infinite number. This group, too, is divided into two parts. Some such as our contemporary Henry of Harclay say that it is composed of an infinite number of indivisibles that are directly joined. But others such as Lincoln [Robert Grosseteste], say [that it is composed] of an infinite number [of indivisibles] that are indirectly joined to one another. Therefore, the conclusion is this: “If one continuum is composed of indivisibles in some way” (the “way” includes any of the precedent ways), it then follows that “any continuum is composed of indivisibles according to a similar way.” [Katz et al, 2016, 178-179]

Bradwardine then presented arguments to reject most of these possibilities. For example, to reject the assumption that the continuum is composed of a finite number of points, he proved:

If this [is true], then the circumference of a circle is double of its diameter. This is: half of the circumference is equal to its diameter. From the different points of the diameter, [assuming that] they are 10, ten perpendiculars are drawn directly to different points on half the circumference. It follows that there are 10 points on half the circumference, because only one point on half the circumference corresponds [to] a perpendicular. Therefore equally, there are the same number of points on half the circumference as are on the diameter. Therefore, according to the second conclusion, half the circumference equals the diameter. [Katz et al, 2016, 179]

Bradwardine realized that this is impossible. Later, he rejected the hypothesis that a continuum is composed of an infinite number of indivisibles:

If this is true, a terminated surface can exceed another surface equal to it by any finite proportion. Let AB and CD be parallel lines. Atop base CE a right-angled parallelogram AFCE is constituted, and atop the same base another parallelogram CGHE is constituted with sides that are as much longer as you want than the sides of the parallelogram AFCE. [See Figure 8.] Then all lines of CGHE which are drawn from all points of CE to the opposite points of GH are equal in number to those points, and consequently to all perpendiculars of AFCE which are drawn from the same points to the opposite points. But they are longer than those [lines]. Therefore, CGHE is larger than AFCE. But according to I 36 of Euclid’s Elements, the parallelograms are equal. [Katz et al, 2016, 180]

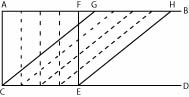
Figure 8. Bradwardine's parallelograms

Bradwardine finally announced his true view of the composition of continua:

No continuum is made up of atoms. From here follows and elicits: Every continuum is composed of an infinite number of continua of the same species as it, […] that is, every line is composed of an infinite number of lines, every surface composed of an infinite number of surfaces, and so on concerning other continua [Katz et al, 2016, 180].

Similarly, Bradwardine investigated four differing theories regarding relationships among speed (V), force (F), and resistance (R) in his Treatise on Proportions. First, he explained and demolished the thinking of Aristotle in On the Heavens and Earth: The proportion between the speeds with which motions take place varies as the difference whereby the power of the mover exceeds the resistance offered by the thing moved. Then he explained and rejected Averroes’ Comment 36 on Aristotle’s Physics Book VI: The proportion of the speeds of motions varies in accordance with the proportion of the excesses whereby the moving powers exceed the resisting powers. Next, he destroyed a generalization built on remarks in Aristotle’s Physics and On the Heavens and from On Weights: With the moving power remaining constant, the proportion of the speeds of motions varies in accordance with the proportion of resistances, and with the resistance remaining constant, it varies in accordance with the proportion of moving powers. Finally, he took apart Comment 79 on Aristotle’s Physics VIII by Averroes: There is neither any proportion nor any relation of excess between motive and resistive powers. Then he began his own contribution.

Now that these fogs of ignorance, these winds of demonstration, have been put to flight, it remains for the light of knowledge and of truth to shine forth. For true knowledge proposes a fifth theory, which states that the proportion of the speeds of motions varies in accordance with the proportion of the power of the mover to the power of the thing moved . . . Furthermore, there does not seem to be any theory whereby the proportion of the speeds of motions may be rationally defended, unless it is one of those already mentioned. Since, however, the first four have been discredited; therefore, the fifth must be the true one. We therefore arrive at the following theorem:

Theorem I. The proportion of the speeds of motions follows the proportion of the force of the mover to that of the moved, and conversely. Or, to put it another way, which means the same thing: The proportion of motive to resistive power is equal to the proportion of their respective speeds of motion, and conversely. This is to be understood in the sense of geometric proportionality. [Katz et al, 2016, 189-190]

Symbolically then, the first theorem can be expressed as \(V={\log}_n(F/R)\) or as \(n^V =F/R.\) That is to say, doubling the velocity squares the ratio of motive power to resistance, tripling the one cubes the other, and so on. For the formula to be correct universally, \(n\) is necessarily a constant equal to \(F/R\) when \(V = 1.\) Although the result is not our modern relationship, Bradwardine was able to use mathematical principles to prove various theorems dependent on his result.

An obvious question here is why, since Aristotle was important both to Muslim scientists, in the translation and adaptation of Averroes, and to Jewish mathematicians, in the Hebrew translations of Averroes, these men never considered the mathematical problems connected with kinematics. Perhaps in both cases these ideas would not be considered important enough religiously to be studied. But more certainly, the ideas of Aristotle were never discussed in a setting in which one could debate these questions. It seems clear from Bradwardine’s style, that it was through disputations that he could demolish certain arguments and therefore come up with one he believed correct.

Another prominent member of the Mertonian school was William Heytesbury (1313-1373). Continuing further the discussion of velocity, he was one of the first to state the Mean Speed Theorem: A body that moves with uniformly accelerating speed traverses in a given time the same distance as a body that in the same time moves with a constant speed equal to the accelerating body’s speed at the middle instant. Heytesbury gave a demonstration of this result by an argument from symmetry, and then proved the easy corollary, that under uniformly accelerated motion from rest, a body in the first half of a given interval will traverse one-third of the distance it covers in the second half of the interval.

Heytesbury’s slightly younger contemporary Nicole Oresme (1320-1382), connected with the University of Paris, made some further advances by using a graphing technique to visualize continuous quantity. As he put it,

[E]very intensity which can be acquired successively ought to be imagined by a straight line perpendicularly erected on some point of the space or subject of the intensible thing, e.g., a quality. For whatever ratio is found to exist between intensity and intensity, in relating intensities of the same kind, a similar ratio is found to exist between line and line, and vice versa. [Katz et al, 2016, 197]

Oresme applied his result to all sorts of “intensities” and drew figures to represent uniform qualities, uniformly difform qualities as well as difformly difform qualities:

[E]very uniform quality is imagined by a rectangle and every quality uniformly difform terminated at zero degree is imaginable by a right triangle. Further, every quality uniformly difform terminated in both extremes at some degree is to be imagined by a quadrangle having right angles on its base and the other two angles unequal. Now every other linear quality is said to be “difformly difform” and imaginable by means of figures otherwise disposed according to manifold variation. [Katz et al, 2016, 199]

This geometric representation enabled Oresme to give a simple geometric proof of the Mean Speed theorem. However, he was a bit puzzled when he tried to apply his methodology to the idea of curvature, because he could not figure out how to compare different curvatures.

For curvature, like the other qualities, has both extension and intensity, and one kind of curvature is uniform while another is difform. But still it is not manifest, in regard to the ratio of the intensity of curvatures, whether one is double another or exists in another ratio to it, or whether or not curvatures are unrelatable one to the other by ratio. [Clagett, 1968, 215]

Oresme wanted to define increase in curvature as a function of “its departure from straightness,” but could not actually measure this. He could certainly tell if one curve was more “curved” than another by looking at whether one could be included in the space between the second and a straight line – but this now involved the whole notion of the angle of contingence, that is, the angle between a circle and its tangent, and it was reasonably clear, even to Oresme, that measurement of these “quantities” was not possible. On the other hand, Oresme noted that “every circular curvature is uniform and vice versa, and every other curvature is difform.” He could measure circular curvature:

Its intensity is measured by the quantity of the radius of the circle whose curve is … the circumference, so that by the amount the radius is less, so proportionally the curvature will be greater [Clagett, 1968, 221].

This was quite an insight for the fourteenth century. However, Oresme was less successful when he tried a counting argument for figuring out the total number of combinations of six simple types of figures representing quality. Although Hebrew writers before Oresme, including both ibn Ezra and Levi ben Gershon, had shown how to calculate such values, Oresme somehow made an error. In fact, combinatorial reasoning was not to be fully developed in Europe for another two hundred years.

While mathematics at the universities was clearly important, with the practitioners delving into philosophical questions coming out of Aristotle, the growth of commerce in Italy beginning in the thirteenth century spawned a different kind of mathematics. The Italian merchants of the Middle Ages generally were what today we might call venture capitalists. They traveled themselves to distant places in the East, bought goods which were wanted back home, then returned to Italy to sell them in the hope of making a profit. These traveling merchants needed very little mathematics other than the ability to determine their costs and revenues for each voyage. By the early fourteenth century, however, a commercial revolution spurred originally by the demands of the Crusades had begun to change this system greatly. New technologies in shipbuilding and greater safety on the shipping lanes helped to replace the traveling merchants of the Middle Ages with the sedentary merchants of the Renaissance. These “new men” could remain at home in Italy and hire others to travel to the various ports, make the deals, act as agents, and arrange for shipping. Thus, international trading companies began to develop in the major Italian cities, companies that had a need for more sophisticated mathematics than did their predecessors. These new companies had to deal with letters of credit, bills of exchange, promissory notes, and interest calculations. Business was no longer composed of single ventures but of a continuous flow of goods consisting of many shipments from many different ports enroute simultaneously. The medieval economy, based in large part on barter, was gradually being replaced by a money economy.

The Italian merchants needed a new facility in mathematics to be able to deal with the new economic circumstances, but the mathematics they needed was not the mathematics of the quadrivium, the mathematics studied in the universities. They needed new tools for calculating and problem solving. To meet this need, a new class of “professional” mathematicians, the maestri d’abbaco or abacists, appeared in early fourteenth century Italy. These professionals wrote the texts from which they taught the necessary mathematics to the sons of the merchants in new schools created for this purpose.

In addition to the algorithms of the Hindu-Arabic number system, the abacists taught their students methods of problem solving using the tools of both arithmetic and Islamic algebra. The texts written by the abacists, of which several hundred different ones still exist, are generally large compilations of problems along with their solutions. These include not only genuine business problems of the type the students would have to solve when they joined their fathers’ companies, but also plenty of recreational problems typical of the kind found in modern elementary algebra texts. There were also sometimes geometrical problems as well as problems dealing with elementary number theory, the calendar, and astrology.  The solutions in the texts were written in great detail with every step fully described, but, in general, no reasons were given for the various steps. Perhaps the teachers did not want to disclose their methods in written form, fearing that then there would no longer be any reason to hire them.  In any case, it seems clear that these abacus texts were designed not only for classroom use, but also to serve as reference manuals for the merchants themselves. A merchant could easily find and readily follow the solution of a particular type of problem without the necessity of understanding the theory.

Among the many extant abacist texts, we consider just the Libro di Ragioni by Paoli Girardi, written in Montpellier in 1327. Of course, Montpellier was not only a university town, but also a center for trade in the south of France. Although Paoli was from Florence, it is therefore not surprising that he travelled to Montpellier.  His text contained not only the basic rules common to such texts, but also some theoretical explanations of rules for solving equations, including the basic al-Khwārizmī rules for quadratics. He tried to appeal to his students by writing the problems as practical ones:

A man loaned 20 lire to another for two years at compound interest. When the end of 2 years came he gave me 30 lire. I ask you at what rate was the lire loaned per month?

There is a man who went on 2 voyages. On the first voyage, he earned 12 denari. On the second voyage, he earned at the same rate that he made on the first voyage, and at the end he found [he had] 100 denari. I ask you with how many denari did he leave?

Interestingly, Paolo did not write his problems so they would have simple whole number answers. The answer to the first problem was that the lire were loaned at the rate of the root of 600 minus 20 denari per month. The answer to the second problem was that the merchant began with the root of 1300 plus 38 denari.

For another example of a 14th century abacist text, see "Mathematical Treasure: Problems from the Zibaldone da Canal."

There were clearly mathematical geniuses in all three of these medieval mathematical cultures, most of whom shared a common mathematical background of the Hindu-Arabic number system, the works of Aristotle, and Euclid’s Elements. Anyone with an interest in mathematics had certainly studied the Elements, and quite possibly knew other works of Euclid. Also, he was familiar with many texts of Aristotle and believed that any philosophical work had to contend with the great philosopher’s thoughts, either by attacking or defending them. Finally, it was the Muslims who brought the Hindu-Arabic system to Europe from the East; the Jews learned it from them; and the Catholics eventually mastered it as well, learning both from translations from the Arabic and from the material Fibonacci brought back from his travels to Muslim lands.

Yet starting with the same basic information, the mathematicians from the three cultures were interested in different mathematics.  Algebra, of course, had been developed in eastern Islam, but it seems that the only algebraic work available in western Islam was that of al-Khwārizmī from the ninth century. The more advanced Muslim algebraic work was not available in Spain, although Fibonacci discovered some of it in his travels. In any case, the Spanish Muslims were not apparently interested in algebra. But as we have seen, there was definite interest in geometry, both practical geometry (which was also of interest to the other cultures) and quite theoretical geometry. Muslim geometers had mastered the basic Greek techniques of proof and did not hesitate to prove all sorts of interesting results. And along with geometry, there was also trigonometry, important for astronomy, which in turn was necessary for religious purposes.

The Jews, too, were not interested in algebra, at least not until the late fourteenth century. Even then, the Hebrew work in algebra was basically limited to material found in al-Khwārizmī. Of course, just as in Islam, quadratic equations were solved earlier in the context of measuring areas and lengths, but the methodology was the older one of manipulation of geometric figures rather than the newer methodology of “things”. On the other hand, Jewish authors seemed to be very interested in geometry. There were quite a few authors who investigated advanced geometric topics, being careful to give strict Euclidean proofs. And there were also several investigations of topics in combinatorics, both intuitively and, in the case of Levi ben Gershon, with careful proofs. Levi and others also investigated some pure number theoretic problems. And, of course, trigonometry was studied, since, as for the Muslims, this was necessary for astronomy and therefore for calendrical questions.

Catholic Europe was interested in mathematics different from the kinds studied by the Jews and Muslims. First, there was more interest in developing algebra beyond al-Khwārizmī. Even Fibonacci had problems from later authors, and certainly Jordanus de Nemore in the thirteenth century developed additional material. Interestingly, however, many of the algebraic techniques developed in eastern Islam did not reach Europe during the medieval period. On the other hand, there was little interest in advanced geometry. Euclid was mastered, and there was some interest in the works of Archimedes, but there was nothing in Catholic Europe like the advanced geometry developed in Muslim Spain. In addition, even though astronomy was part of the medieval university curriculum, there was little development of trigonometry beyond what was already known in Greece. It was not until the work of Regiomontanus in the mid-fifteenth century that Catholic Europe had a trigonometric work comparable to the works written in Muslim Spain centuries earlier. Probably one of the reasons for this was that astronomy was not nearly so important for calculations involving the Julian calendar as it was for both the Muslim and Jewish calendar. Similarly, the subject of combinatorics, of interest to the Jews and to the Muslims of North Africa, was barely mentioned by Catholic mathematicians, although Jordanus de Nemore did display the Pascal triangle as part of a discussion of ratios. The most important mathematical topic studied in Catholic Europe – and not in Muslim or Jewish Europe – was the set of developments coming out of the study of Aristotle’s physical theories. In particular, as we have noted, mathematicians in Oxford and Paris were very interested in the ideas of motion, and it was the study of kinematics as well as mechanics that was crucial for the work of Galileo and others during the Renaissance.

Although mathematical geniuses existed in each of the three religious groups we have considered, men who could successfully attack any interesting problem, it seems clear that the culture in which they lived was crucial in their actual choice of problems to consider.  We can see in this study of mathematics in medieval Europe, as in other times and places, that mathematics is not, and indeed cannot be, a culture-free subject.

Acknowledgment

This article is a revised version of a plenary address given at the 2016 meeting of the International Study Group on the Relations Between History and Pedagogy in Montpellier, France.

About the Author

Victor J. Katz is Professor Emeritus of Mathematics of the University of the District of Columbia; founding co-editor (with Frank J. Swetz) of MAA Convergence; author of History of Mathematics: An Introduction (3rd ed., 2009), widely recognized as the definitive general history of mathematics text for professionals, instructors, and students; and editor of two sourcebooks for history of mathematics, The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (2007) and Sourcebook in the Mathematics of Medieval Europe and North Africa (2016), the latter referenced in this article. - Janet Beery, Editor, MAA Convergence

Clagett, M. (1968). Nicole Oresme and the medieval geometry of qualities and motions. Madison: University of Wisconsin Press.

Freudenthal, G. (1995). Science in the medieval Jewish culture of southern France. History of Science 33, 23-58

Garcia-Ballester, L., Ferre, L., & Feliu, E. (1990). Jewish appreciation of fourteenth-century scholastic medicine. Osiris 6, 85-117.

Huff, T. E. (1993). The rise of early modern science: Islam, China, and the West. Cambridge: Cambridge University Press.

Ibn Ezra, Abraham (1995). The Secret of the Torah: A Translation of Abraham Ibn Ezra’s Sefer Yesod Mora Ve-Sod Ha-Torah. Translated by H. N. Strickman. New York: Jason Aronson, Inc.

Katz, V. J., Folkerts, M., Hughes, B., Wagner, R., & Berggren, J. L., eds. (2016). Sourcebook in the Mathematics of Medieval Europe and North Africa. Princeton: Princeton University Press.

Leonardo Pisano Fibonacci (1987). The Book of Squares. Edited and Translated by L. E. Sigler. Boston: Academic Press.

Sā‘id al-Andalusī (1991). Science in the medieval world: Book of the categories of nations. Translated and edited by Semar’an I. Salem and Alok Kumar. Austin: University of Texas Press.

Wartenberg, Ilana (2015). The Epistle of the Number by Ibn al-Aḥdab: The transmission of Arabic mathematics to Hebrew circles in medieval Sicily. Piscataway, NJ: Gorgias Press

Editor's note: In addition to those mentioned elsewhere in this article, the following Convergence articles describe mathematics and mathematical cultures in medieval Europe:

• Victor Katz, "Recreational Problems in Medieval Mathematics" (December 2017)
• Betty Mayfield, "Gerbert d'Aurillac and the March of Spain: A Convergence of Cultures" (2006)
• Richard Pulskamp and Daniel Otero, "Wibold's Ludus Regularis, a 10th Century Board Game" (June 2014)
• Randy K. Schwartz, "'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript" (July 2012)